Rekommenderad från: 15 år
[kkratings]
Det finns en rutig remsa 1xn:
Anders och Filip spelar ett spel. De turas om att göra drag: Anders får sätta ett kryss i en tom ruta och Filip får sätta en ring i en tom ruta. Dock får inte två kryss hamna bredvid varandra och inte heller två ringar. Spelaren, som inte kan göra ett drag när det är hans tur, förlorar.
Anders gör det första draget. Vem har ett vinnarstrategi, det vill säga vem kan alltid vinna oavsett hur motståndaren spelar?
Observera att svaret kan bero på talen n, som säger hur lång remsan är.
Tehuset
Rekommenderad från: 13 år
[kkratings]
55 indier och turkar träffades på ett tehus. Varje person drack antingen te eller kaffe. När en indier dricker te så talar hen alltid sanning och när hen dricker kaffe så luras hen alltid, medan turkarna är precis tvärtom. På frågan ”Dricker du kaffe?” svarade 44 personer ”ja”, ”Är du en turk?” svarade 33 personer ”ja” och på frågan ”Regnar det ute?” svarade 22 personer ”ja”. Hur många indier drack te på tehuset?

Ett matematiskt korttrick
Rekommenderad från: 12 år
[kkratings]
En trollkarl med förbundna ögon och hans assistent utför följande trick. Trollkarlen har 29 kort med talen 1 till 29 på. Han ger korten till någon person i publiken, som väljer ut två av dem. Resten av korten ges till assistenten, som sedan väljer två av de resterande korten och visar till personen i publiken. Personen läser upp högt båda talen för trollkarlen (i vilken ordning han vill). Därefter gissar trollkarlen vilka kort som personen valde ut i början.
Hur skall trollkarlen och assistenen förbereda sig för att alltid lyckas med tricket?

Att täcka över en svart kvadrat
Rekommenderad från: 10 år
[kkratings]
På ett papper finns en bild på en svart kvadrat. Du har tillgång till 7 kvadratformade brickor av samma storlek som den ritade kvadraten. Hur ska du göra för att täcka över kvadraten med brickorna så att inga brickor ligger på varandra och varje bricka täcker åtminstone en liten del av kvadraten (åtminstone en punkt inuti)?

Uppdelning i nästan lika heltal
Rekommenderad från: 15 år
[kkratings]
På hur många sätt kan man skriva talet 2009 som en summa av några positiva nästan lika heltal? Talen kallas nästa lika om deras skillnad är (till beloppet) maximalt 1. Sätten betraktas som samma om det enda som skiljer dem åt är ordningen på termerna.
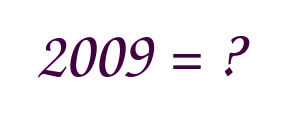
Symmetrisk figur
Rekommenderad från: 10 år
Förkunskaper: spegelsymmetri
[kkratings]
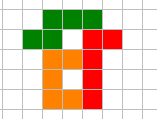
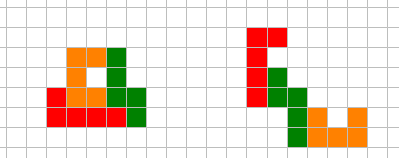
Bygg ihop bitarna nedan till en spegelsymmetrisk figur. Varje bit skall användas exakt en gång.
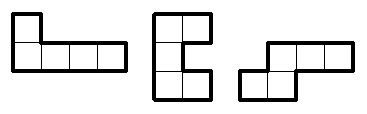
Klassiska bevis: Monges sats
Om du precis har börjat intressera dig för matematik, då säger jag grattis! Du kommer att bli fascinerad av problem, teorier och bevis många gånger!
Det är inte lika lätt om man fått matematiken serverad på ett guldfat sedan barnsben (eller tonårsben). Ju längre tid som går, desto mer måste man lära sig för att bli imponerad av något nytt tankesätt. Men som pris får man oftast upptäcka något ännu mer fascinerande än förra gången.
Ett av de här tillfälen var jag med om när jag för första gången besökte Uppsala. Det var någon gång vid årsskiftet 2001/2002 och jag gick i ettan på gymnasiet och kunde förstås inte så mycket om universitetsmatematik. Vilket i och för sig inte behövs för historien. Men snart får ni se hur allt ändå hänger ihop.
Vi fick sitta i ett klassrum och en matematiker berättade följade problem för oss.
Tre olika cirklar ligger i planet och de skär inte varandra (och ligger inte inuti varandra heller). För varje par av cirklar dra två linjer, som tangerar båda två cirklarna. Om cirklarna är olika stora, kommer dessa två linjer att skära varandra. Frågan är nu: kommer de tre erhållna skärningspunkterna att ligga på samma linje?
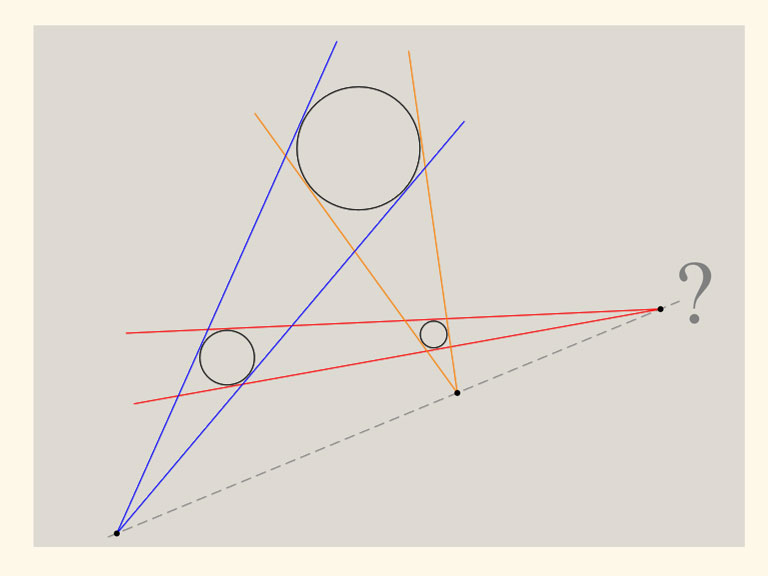
Det visar sig att de måste. Försök att lösa problemet med den geometrin du kan. Det verkar vara svårt att visa, genom att bara rita linjer och bestämma vinklar i planet.
Däremot finns en elegant lösning, som använder sig utav en tredje dimension!
Varför och hur?
Det är en väldigt imponerande idé, att gå högre upp än vad som verkar behövas. Om problemet inte kan lösas, så skall man försöka att titta på det ur en annan synvinkel. Men oftast ligger svårigheten i att välja rätt synvinkel.
Just att gå upp i högre dimensioner visade sig vara nyttigt även i andra vetenskaper. Mycket förklarades av insikten om att jorden är sfärisk, extra dimensioner behövs för att strängteorin skall hålla. Även min forskning handlar om att förstå enklare strukturer genom att titta på de mer kompilcerade. Men hur hjälper den tredje dimensionen i vårt problem?
Föreställ er att det inte är cirklar, utan klot som ligger på ett plant papper, då ser det hela precis ut som på bilden om vi kollar uppifrån. Linjerna är fortfarande linjer, men i rymden kan vi faktiskt konstruera oändligt många linjer som är gemensamma tangenter till två av kloten. Alla dessa gemensamma tangenter bildar en kon, som har sin spets i papprets plan. Spetsen är då även skärningspunkten för de ursprungliga två linjerna.
Men om det finns tre kulor, så är det inte bara så att alla kan läggas på ett papper, vi kan lägga ett plant papper ovanpå dem också! Det pappret tangerar alla kloten, och det har lika mycket rätt att innehålla konspetsarna som det undre planet hade.
Således finns konspetsarna, det vill sägga de erhållna tre punkterna i båda planen. Och två plan skär varandra i en linje! Alltså ligger punkterna på en och samma linje.
Nu kan vi alltså glömma bort hela tredje dimensionen-grejen. Vi har visat att de tre punkterna ligger på samma linje i det tvådimensionella planet.
Här kan ni även titta på en film som illustrerar lösningen.
Tallskogen
Rekommenderad från: 12 år
[kkratings]
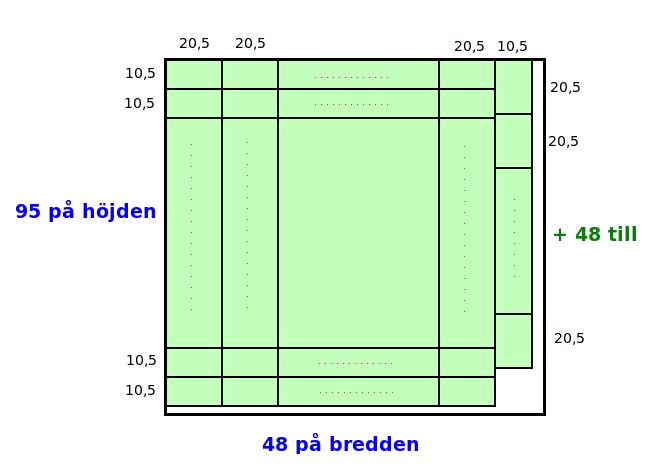
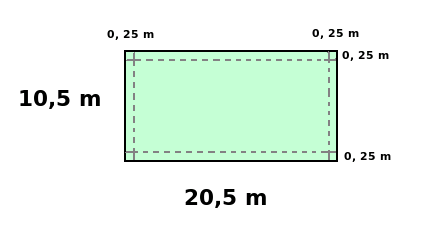
På ett område 1km x 1km växer en tallskog. Alla tallarna har diametern 50 cm. Visa att en fältbiolog kan hitta en ledig rektangel 10m x 20m i skogen, för att kunna sola där med alla sina vänner om det finns a) 1200 b) 4200 c) 4500 d) 4600 träd i skogen.

Ett hekto socker
Rekommenderad från: 12 år
[kkratings]
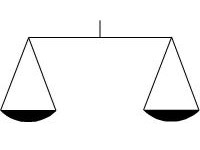
En balansvåg har två skålar. Om tyngderna på skålarna är lika visar balansvågen jämvikt. Annars visar den vilken skål som är tyngre.
Det finns en stor påse strösocker, en balansvåg samt en vikt på 1g. Hur kan man snabbast väga upp ett hekto strösocker? Observera att om man lägger två sockerhögar i en och samma skål, så blandas sockret ihop. Sockerhögarna får sparas mellan vägningarna.
Snigelns underbara resa
Rekommenderad från: 15 år
[kkratings]
 En dag bestämde sig en snigel för att starta en resa. Snigeln rörde sig framåt längs med en rak sträcka i 6 minuter tills det var nog för dagen. Under den tiden kom några människor och tittade på snigels underbara resa. Hela tiden var snigeln betraktad av åtminstone en människa. Det visade sig att varje människa kollade på snigeln i exakt 1 minut och under den tiden kröp den exakt 1 meter. Hur mycket kunde snigeln maximalt krypa under den dagen?
En dag bestämde sig en snigel för att starta en resa. Snigeln rörde sig framåt längs med en rak sträcka i 6 minuter tills det var nog för dagen. Under den tiden kom några människor och tittade på snigels underbara resa. Hela tiden var snigeln betraktad av åtminstone en människa. Det visade sig att varje människa kollade på snigeln i exakt 1 minut och under den tiden kröp den exakt 1 meter. Hur mycket kunde snigeln maximalt krypa under den dagen?
Förtydliganden: För det första så betraktade varje människa snigeln bara under resans gång. För det andra, så kollade varje människa på snigeln 1 minut i sträck och inte utspritt hur som helst.
© 2009-2025 Mattebloggen

 eller
eller De fortsätter spela under tillåtna regler (aldrig två kryss eller två ringar bredvid varandra). Låt oss säga nu att Filip på något sätt lyckas förlora. Det betyder att han i en viss situation har ingenstans att sätta sin ring och de har precis varit Anders tur.
De fortsätter spela under tillåtna regler (aldrig två kryss eller två ringar bredvid varandra). Låt oss säga nu att Filip på något sätt lyckas förlora. Det betyder att han i en viss situation har ingenstans att sätta sin ring och de har precis varit Anders tur.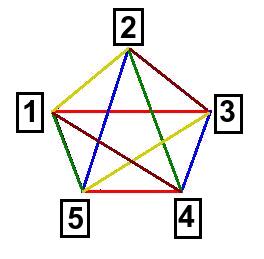
 Till exempel så är följande kanter bruna: den som binder ihop 2 & 3, samt den som binder ihop 1 & 4. Ifall assistenten ser att åskådaren plockar bort korten 2 och 3, så pekar han på korten 1 & 4 och trollkarlen kan då komma ihåg att kanten 1 & 4 hade den bruna färgen och säga exakt vilka kort som plockades bort från början (de som också hade den bruna färgen).
Till exempel så är följande kanter bruna: den som binder ihop 2 & 3, samt den som binder ihop 1 & 4. Ifall assistenten ser att åskådaren plockar bort korten 2 och 3, så pekar han på korten 1 & 4 och trollkarlen kan då komma ihåg att kanten 1 & 4 hade den bruna färgen och säga exakt vilka kort som plockades bort från början (de som också hade den bruna färgen).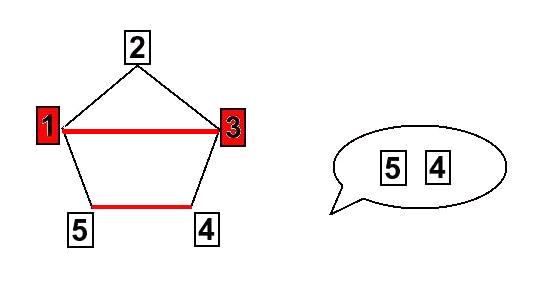
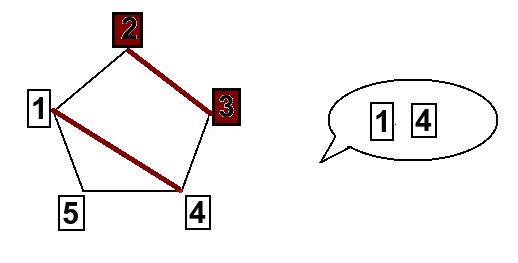
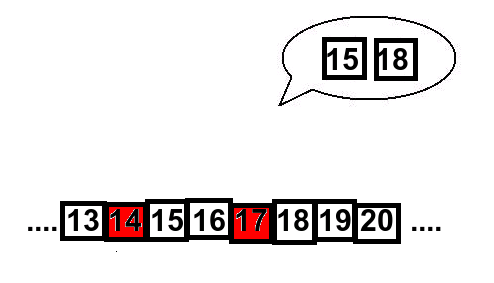 Om de valda korten ligger bredvid varandra, så pekar assistenen på två kort som också ligger bredvid varandra, nämnligen de två som kommer direkt efter. Här är ett exempel:
Om de valda korten ligger bredvid varandra, så pekar assistenen på två kort som också ligger bredvid varandra, nämnligen de två som kommer direkt efter. Här är ett exempel: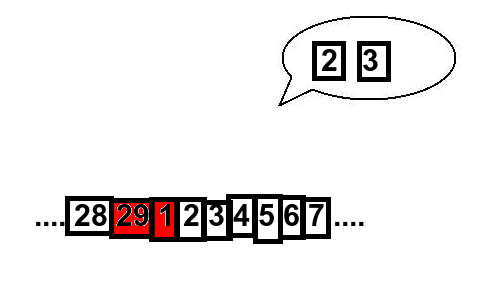
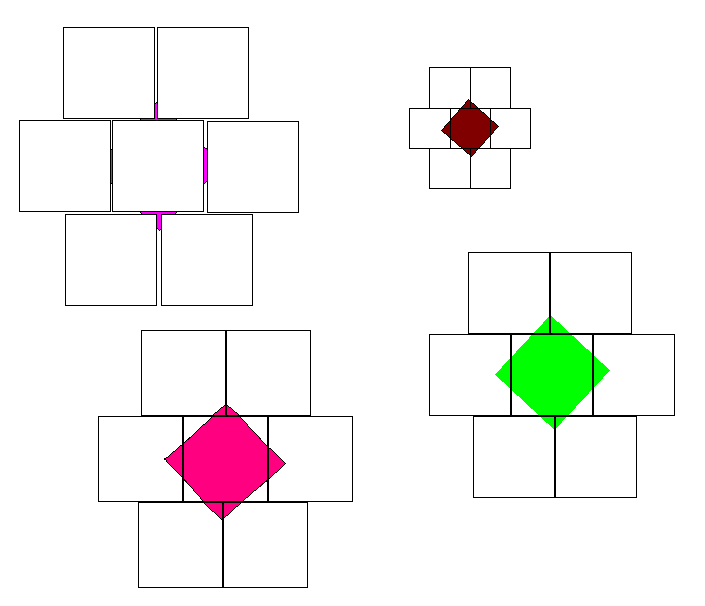
 Idén är att utnyttja tiderna maximalt: snigeln rör sig jättefort när bara människa kollar på den. Annars, om det inte är start- eller slutminut, så står snigeln stilla (och vilar). Klart!
Idén är att utnyttja tiderna maximalt: snigeln rör sig jättefort när bara människa kollar på den. Annars, om det inte är start- eller slutminut, så står snigeln stilla (och vilar). Klart!