Mattebloggen

Lösningen till problemet för de yngre vecka 46

Mattegåta

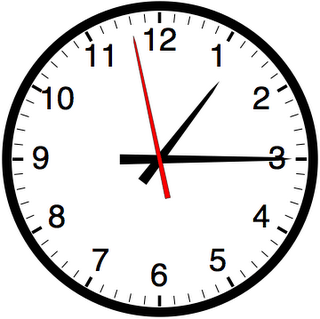
När Dag tog studenten, fick han en klocka som hade en timvisare, en minutvisare och en sekundvisare. Hur många gånger per dygn sammanfaller alla tre visarna? (Förklara varför.)

Diskussion

Det här var ett svårt problem. Ett förvirrande faktum är vi måste studera tiden i dubbel bemärkelse. Problemet hade egentligen varit densamma ifall tre löpare hade sprungit med olika hastigheter runt en bana. Vi undrar när alla tre träffas, så vi kommer betrakta visarna som löpare.

Hur snabba är de då? Sekundvisaren är snabbast och ”springer” med hastigheten ett steg per sekund (stegen är de 60 markeringarna på klockan). Sedan kommer minutvisaren som tar en sextiondedels steg per sekund och långsammast är timvisaren, som ”promenerar” med hastigheten 1/720 steg per sekund (5 steg per timme eller 60 steg på 12 timmar). Nu kan vi pilla med hastigheterna om vi vill för att se när de olika visarna träffar varandra.

Lösning

Vi kan börja med att undersöka när två av visarna, minutvisaren och timvisaren, träffar på varandra under ett dygn. De börjar klockan 0:00 på samma ställe, på tolvan, och sedan rycker minutvisaren iväg. Eftersom minutvisaren klarar av 60 steg på en timme, medan timvisaren tar 5 steg, kommer de att träffas nästa gång efter mer än 1 timme. Mer exakt tar det faktiskt 12/11 av en timme. Minutvisaren drar iväg sedan och kommer gå om timvisare med jämna mellanrum.

Så minut- och timvisaren träffas:
1. efter 0 timmar (de börjar på samma ställe)
2. efter 1 och 1/11 timme
3. efter 2 och 2/11 timme
4. efter 3 och 3/11 timme
5. efter 4 och 4/11 timme
6. efter 5 och 5/11 timme
7. efter 6 och 6/11 timme
8. efter 7 och 7/11 timme
9. efter 8 och 8/11 timme
10. efter 9 och 9/11 timme
11. efter 10 och 10/11 timme
12. efter 11 och 11/11 timme = 12 timmar
13. efter 13 och 1/11 timme
14. efter 14 och 2/11 timme
15. efter 15 och 3/11 timme
16. efter 16 och 4/11 timme
17. efter 17 och 5/11 timme
18. efter 18 och 6/11 timme
19. efter 19 och 7/11 timme
20. efter 20 och 8/11 timme
21. efter 21 och 9/11 timme
22. efter 22 och 10/11 timme
23. efter 23 och 11/11 timme = 24 timmar, vilket är ett nytt dygn, så det räknas inte!

Så minutvisaren och timvisaren träffas 22 gånger per dygn, men vilka av gångerna hakar sekundvisaren på?

Vi kan kolla på vilka positioner sekundvisaren hamnar efter perioder på 1 och 1/11 timme. Sekundvisaren har hastigheten 3600 steg per timme, så totalt kommer den gå en massa varv plus 3600/11 steg som är lika med 327 och 3/11 steg som är lika med 5 varv och 27 och 3/11 steg. Så på klockan kommer visaren att hamna mellan femman och sexan nånstans. Vi kollar alla situationer då timvisaren sammanföll med minutvisaren:

1. sekundvisaren är på 0 steg = prick på klockan 12!
2. sekundvisaren är på 27 och 3/11 steg = mellan kl 5 och kl 6
3. sekundvisaren är på 54 och 6/11 steg = mellan kl 10 och kl 11
4. sekundvisaren är på 21 och 9/11 steg = mellan kl 4 och kl 5
5. sekundvisaren är på 49 och 1/11 steg = mellan kl 9 och kl 10
6. sekundvisaren är på 16 och 4/11 steg = mellan kl 3 och kl 4
7. sekundvisaren är på 43 och 7/11 steg = mellan kl 8 och kl 9
8. sekundvisaren är på 10 och 10/11 steg = mellan kl 2 och kl 3
9. sekundvisaren är på 38 och 2/11 steg = mellan kl 7 och kl 8
10. sekundvisaren är på 5 och 5/11 steg = mellan kl 1 och kl 2
11. sekundvisaren är på 32 och 8/11 steg = mellan kl 6 och kl 7
12. sekundvisaren är på 59 och 11/11 steg = 60 steg = 0 steg = prick på klockan 12!
Sedan upprepar historien sig!

Ingenstans, förutom klockan 12 på natten och på dagen hamnar sekundvisaren ens mellan rätt siffror (t.ex. i situation 8 är sekundvisaren mellan kl 2 och kl 3, medan minut- och timvisaren är mellan kl 7 och kl 8). Detta betyder att alla tre visarna träffas exakt två gånger per dygn!

Adventspyssel 2

Sifferrebus

Oskar ställde upp en multiplikation, men sedan döljde uträkningen genom att byta ut siffror mot bokstäver (likadana siffror byttes ut mot samma bokstav och olika byttes ut mot olika). En siffra 9 blev dock kvar.

Kan du återställa uträkningen?

Visa svaret

Adventspyssel 1

Pappersark

Klipp ut en sådan här figur ur en A4:

Visa svaret

Lösningen till problemet för de äldre vecka 46

Mattegåta

Visa att varje andragradspolynom kan skrivas som en summa av två andragradspolynom, vars diskriminanter är lika med 0.

Diskussion

Vad var en diskriminant? För ett polynom Ax²+Bx+C är det talet B²-4AC.

Ifall diskriminanten är positiv, så har ekvationen Ax²+Bx+C=0 två reella rötter. Ifall den är negativ, så har ekvationen inga reella rötter. Om diskriminanten är 0, har ekvationen exakt en reell lösning.

Bilden illustrerar hur graden för ekvationen kan se ut i de olika fallen (D betecknar diskriminanten).

Nu när vi har koll på diskriminanten, kan uppgiften lösas grafiskt eller algebraiskt, vilken man nu föredrar. Nedan är en algebraisk lösning presenterad.

Lösning (av Benjamin Fayyazuddin-Ljungberg)

Låt P(x) vara polynomet vi vill skriva som summan av två andra polynom. Om P(x) = Q(x) + R(x) är kP(x) = kQ(x) + kR(x). Om Q(x) har diskriminant noll har kQ(x) också det. Därför kan vi utan inskränkning anta att P(x) har koefficienten 1 framför x²-termen.

Nu betraktar vi tre fall:

1) P(x) har diskriminant noll. Då har vi inga problem: P(x) = P(x)/2 + P(x)/2

2) P(x) har negativ diskriminant, det kan skrivas som (x-a)² + k² för någon konstant k. Låt z=x-a, så P(x) = z² + k². Då kan vi skriva P(x) som (z+k)²/2 + (z-k)²/2 = (x-a+k)²/2 + (x-a-k)²/2. Det är tydligt att de här polynomen bara har ett nollställe var, alltså är diskriminanten noll.

3) P(x) har positiv diskriminant, det kan skrivas som (x-a)² – k² för någon positiv konstant k. Låt z = x-a igen. Då är P(x) = z² – k². Vi skriver P(x) som 2(z-k/√2)² – (z-k√2)² = 2(x-a-k/√2)² – (x-a-k√2)². Dessa har också bara ett nollställe var, så de har diskriminant noll.

HMT-kval 2010

Som traditionen är, rättar elever som gått på Danderyds Gymnasium tävlingen HMT varje år. Även elever som gick ut gymnasiet för mer än 6 år sedan…

I helgen rättade vi alla inskickade bidrag och jag fick äran att vara med och rätta uppgift nummer 2 av kvalets problem.

Största delen av rättningen bestod i att rätta ner poängen från maximala 3 till 1 eftersom endast rätt svar (även med kontroll) skulle ge exakt 1 poäng.

Det viktiga i tävlingen är att man kan motivera sina lösningar, och motiveringen motsvarar oftast den större delen av poängen, vilket många elever och lärare tyvärr missar.

Det är ju på samma sätt i livet: det viktigaste är inte resultat, utan vägen dit. Nåväl, nog om livsfilosofi.

Efter rättningens slut bestämdes ett gränspoäng för elever som skulle gå vidare till final. Jag vill gratulera Toomas Liiv, en av de aktiva problemlösarna här på bloggen, som klarade den gränsen! Grattis!!!

Matteproblem för de yngre vecka 47

Mattegåta

I ett visst spel används mynt som är värda 1, 15 och 50 Hello Kitty-dollar. En spelare köpte ett svärd och fick i växel ett mynt fler än vad han betalade. Vilket är det minsta antalet dollar som svärdet kunde kosta?

Lösningen till problemet för de yngre vecka 45

Mattegåta

En chokladtårta är rektangelformad och sju personer ska dela på den. På tårtan finns 7 marsipanrosor:

Hur kan man dela tårtan i sju delar så att det finns en ros i varje del, om man bara får skära tårtan tre gånger och skärningarna måste vara raka linjer? Observera att delarna inte behöver vara lika stora.

Diskussion

Om det till en början inte verkar gå med tre linjer, tänk på vad tre linjer kan bilda för konfigurationer vid sidan av tårtan. Tre linjer som inte korsar varandra i en och samma punkt och som inte är parallella bildar en triangel och sex oändliga delar om de ritas på ett oändligt plan.

Sju är det maximala antalet delar, så linjerna på tårtan ska bilda någon liknande figur (det ska vara en ros i varje del).

Ett annat sätt att komma fram till svaret är att rita en linje i taget. Om man tänker från slutet, måste varje del på tårtan innehålla högst två rosor innan sista linjen ritas (så att den eventuellt skär på dessa delar). På samma sätt, måste varje del innehålla högst fyra rosor innan den andra linjen ritas. Så den första linjen som ritas måste dela tårtan i två delar: en med tre rosor och en med fyra.

Lösning (av Nicklas Yttergren)

Så här till exempel:

Matteproblem för de äldre vecka 47

Mattegåta

I tio likdana kannor finns lite mjölk: varje kanna är full till max 10%. En tillåten operation är att ta en valfri kanna och hälla av en del av mjölken till de andra kannorna (lika mycket till varje övrig kanna).

Visa att 10 operationer räcker för att få kannorna att innehålla exakt lika mycket mjölk.

Lösningen till problemet för de äldre vecka 45

Mattegåta

Ett biljardbord har en långsida som är dubbelt så lång som kortsidan. I varje hörn finns det ett hål, samt två hål till finns på varje långsidas mitt.

Vilket är det minsta antalet bollar som man kan placerat ut på bordet så att varje hål befinner sig på samma linje som ett visst par av bollar? (Bordet är rektangulärt, hål och bollar antas vara lika stora som punkter.)

Diskussion

Eftersom det frågas efter det minsta antalet i uppgiften är det underförstått att resultat skall bevisas. Det vill säga det måste finnas ett exempel med x bollar (om x är svaret), samt bevis för att det inte går med färre än x bollar.

Ett sätt att jobba på är att börja underifrån (till exempel med 1 eller 2 bollar) och för varje antal antingen visa att det inte går eller att det går. Fallen är oftast svårare närmast svaret. Lite som i fyrfärgsproblemet!

Fyrfärgsteoremet

Sats. För en platt ”karta” räcker det alltid med fyra färger för att måla ”länderna” på kartan så att inga två länder med gemensam gräns har samma färg (gränser utgörs av raka eller krokiga linjesegment).

Det var länge känt att det räckte med fem färger och att det finns kartor som inte går att färga med tre färger. Men fallet fyra tog lång tid tills den äntligen bevisades med hjälp av datorberäkningar.

Lösning (av Erik Svensson)

Till att börja med kan vi uppenbart utesluta att det går med bara en boll (och förstås även med noll bollar).

Det finns ej heller någon lösning för två bollar, ty vi vet att två bollar (punkter) entydigt bestämmer en linje, så om samtliga hål ska ligga i linje med två bollar, då måste alla hålen ligga på samma linje. Men hålen på biljardbordet ligger inte på en linje.

Det är inte heller möjligt med tre bollar, vilket vi ser om vi försöker konstruera en. Om vi har tre bollar, då finns det två möjligheter: Att de ligger på en linje eller att de inte gör det.

Ifall de ligger på en linje, då får vi en motsägelse med samma resonemang som för två bollar, och ifall de inte ligger på en linje så bildar de en triangel. I så fall utgör varje linje med två bollar en sida i denna triangel, och bollarna är hörnen.

Vi börjar med att konstatera att ingen sida i denna triangel kan täcka tre hål, ty de enda linjerna på bordet som täcker tre hål är långsidorna. Ens om vi antar att frågeformuleringen tillåter bollar längs med sidorna innebär detta att två bollar måste ligga på en av långsidorna, vilket innebär att den tredje bollen måste ge upphov till två linjer som täcker samtliga tre resterande hål, vilket medför att någon av dessa två linjer måste täcka två hål på den andra långsidan och ändå korsa den första långsidan, vilket är omöjligt.

Att täcka fyra eller fler hål med en linje är förstås också omöjligt som biljardbordet är uppbyggt.

En linje kan ej heller passera genom bara ett hål, eftersom detta lämnar fem hål att täckas med de resterande två linjerna, och alltså måste någon av dessa linjer täcka minst tre hål, vilket motsäger det vi just kom fram till. Även en linje som inte täcker några hål kan vi utesluta, eftersom denna linje i så fall kan tas bort och därmed ge en lösning för två hål, vilket vi visat inte existerar.

Således måste vi ha tre linjer som täcker exakt två hål, och de måste täcka två bollar vardera. Eftersom varje boll är ett hörn i den triangel som bildas ligger varje boll på två sådana linjer.

På bilden ser vi alla möjliga linjer som täcker två hål, samt alla skärningspunkter mellan dem. Dessa punkter är de enda kandidaterna till var en boll kan ligga. Vi ser emellertid att det inte finns någon triangel av sådana punkter (med de utmarkerade linjerna som sidor), och den minsta slutna figur vi kan bilda är en fyrhörning. Alltså finns det ingen lösning för tre bollar, men det finns en för fyra, till exempel genom att välja fyra punkter som bildar en fyrhörning i bilden och lägga bollarna där.

Svenska skolböcker

Som privatlärare börjar jag sätta mig in i de svenska matteböckernas värld. Själv gick jag bara ett år på svenska högstadiet och då fick jag hålla på med egna matteböcker.

Skillnaderna i 5:ans mattebok och 8:ans mattebok vad gäller pedagogiken är inte så påfallande stora. Men jag märker att 8:orna har blivit inskolade väldigt hårt medan 5:orna inte ännu hunnit bli det (men är på god väg!).

Jag syftar på uppgifternas struktur. Uppgifterna är nyttiga och faktiskt rätt så bra, men alldeles för många är alledeles för triviala!

Inte triviala i den meningen att de löses direkt av vilken elev som helst. Men de är triviala för vuxna. Det beror på att nästa alla dem löses med 1 steg. Eller med 1 formel. Eller med 1 metod.

Så fort uppgiften ska lösas med 2 steg (eller gud bevare, fler), blir eleverna rätt så vilsna. Ett exempel jag och en åtta höll på med senast (en av de svårare uppgifterna i läxan) gick ut på att få fram vissa vinklar från en bild, x och y. Efter ett tag fick vi fram:
x+y = 180
x+36 = 180

Då säger pojken, att han vet, hur man ska få fram x, men han vet inte hur man ska få fram y. Han hade aldrig löst exakt en sådan uppgift förut. Så han har inte den exakta metoden i fickan just för den här uppgiften. Och den här (ganska bra) uppgiften är inte uppdelad i steg! Panik!

En liknande upplevelse hade min pojkvän för ett tag sedan. Han skulle förklara för någon att arean på en viss triangel var ”basen gånger höjden genom två” och då svarade eleven: ”ahaaa, det är alltså ’gånger'” som om han/hon lärt sig nu att det var faktiskt ”gånger” som skulle plockas fram från någon sorts virtuell verktygslåda när traingelareauppgifter kom.

Barnet har lärt sig receptet, barnet har lärt sig att avkoda uppgifterna i boken, således kan barnet lyckas i matte i svenska skolan. Om 90% av uppgifterna består av ett enda steg, varför ska då eleverna förvänta sig något annat.

En jättebra video med en TED-talk på samma tema. Talaren Dan Meyer talar inte bara om problem, utan också om möjliga lösningar!

Patient Problem Solving