Rekommenderad från: 12 år
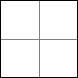
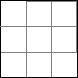
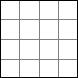
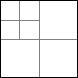
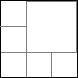
Visa att en kvadrat kan delas upp i n stycken mindre kvadrater för alla n>5. Med ”att dela upp” menas att vi klipper en kvadrat så att alla erhållna delar också är kvadrater och det blir inga bitar över.
Induktion (matematisk sådan)
Från Wikipedia: Låt P(n) vara ett påstående som har att göra med ett positivt heltal n, och antag att följande påståenden är sanna:
- P(1) är sant.
 .
.
Då är påståendet P(n) sant för varje val av det positiva heltalet n.
Lätt som en plätt, eller?
Alla tycker induktion är svårt
Alla som någonsin har varit lärare i grundläggande matematikkurser på universitet har stött på svårigheter inom ett specifikt avsnitt: induktion. Det har skrivits många kompendieinlägg och artiklar i ämnet, det går att hitta massvis med förklaringar och exempel, men ändå har så många så svårt för det. Varje år är det kanske 30 elever man har och 29 av dem har svårigheter med induktion.
Nyligen fick jag ett mail som bad om hjälp med en induktionsuppgift. Problemet för personen var att det inte var en standarduppgift (som handlar om summor, vänsterled=högerled, etc.), och fattar man inte induktionsprincipen då, så är man fast.
Vad induktion inte är
För att börja kasta lite ljus över ämnet, kan jag berätta om vad induktion inte är.
1. Det är inte en metod. Det påminner om en metod väldigt mycket, ”stoppa in basvärden här”, ”skriv induktionsantagandet där”, ”härled induktionssteget mha induktionsantagandet”. Jag tror det är det som förklaringen av induktionsprincipen faller på. Den förklaras mycket formellt, precis som en metod, och därför också uppfattas som sådan. Finns alltså inget sätt att lösa allmännt induktionsproblem!
2. Det är absolut inte en formel. Om man bara har sett summationsuppgifter, säg ”Visa att summan av de första n positiva heltalen är n(n+1)/2” och liknande, tror man kanske att induktionspincipen är en slags formel. Man stoppar in lite summor här och var och blir det likhet, så är man klar. Så är det på sätt och vis med summationsuppgifter, dock faller inte alla de ut lika lätt som exemplet jag tog upp.
3. Det är inte en sats, en teori, en bok, en tupp osv.
Var är det då? Induktionen är en princip, ett axiom och så önskas. Det betyder att det är någonting som vi människor (matematiskt lagda) tycker borde gälla. Det är någonting som följer logikens lagar. Till exempel ”äpplet faller inte långt från trädet” är ett av naturens lagar och det är lite konstigt att titta på det som en metod för beräkning av äpplenas banor. Ett mer matematiskt exempel är ”Om det finns en linje i planet och en punkt utanför linjen, så kan man bara rita en linje genom punkten som är parallell med den första, ändrar man något så kommer första linjen korsas”. Det är ju ganska naturligt att det är så, men det är fortfarande varken metod eller formel.
Hur jag lärde mig induktion
Det skedde relativt tidigt, då jag ännu inte fattade mig på summationstecknet, vilket nog hjälpte för att förstår principen bra (kanske det som är lösningen, lära ut summa efter att man lär ut induktion på grundläggande algebra-kursen?). Jag fick några problem på fritiden, så jag försökte klura ut hur man löste dem. Men det är väldigt svårt att komma på principen själv, så jag lyckades inte först. Sen när man förstår principen så säger det ”klick” och sådana problem löses på bara några minuter.
Och hur förstår man principen då? Jo, genom exempel! Exempel från matten eller vardagen spelar ingen roll. Vitsen är att när någon berättar att man visar någonting att börja med (bas) och sedan visar att ”varje leder till nästa” (induktionssteg), så är det klart att det följer för alla. ”Självklart måste det vara så!”, säger man då, och då har man förstått. Nästa svåra steget är att översätta lösningar till matematikspråket. Just ”översätta”, eftersom mitt största råd är att lösa varje uppgift med ord först, så gott det går, och bara sedan försöka formalisera. Till att börja med: glöm bort vad induktion är och försök lösa de här, så återkommer jag med utförliga exempellösningar.