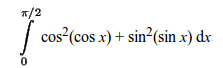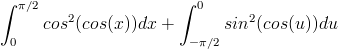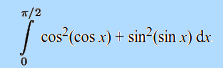integral – Mattebloggen

Vilket är värdet av följande integral?

Uttrycket under integralen ser ju lite hemskt ut. Tillämpa då en av de viktigaste reglerna i matte:

Ser du något hemskt, gör variabelbyte!

Men vilket variabelbyte skall göras? Det som skulle passa oss i slutet är någon form av trigonometriskt samband som skulle förenkla integralen.

I vårt fall har vi något som liknar ”trigonometriska ettan” så det får vi sträva efter.

För en godtycklig vinkel $\alpha$ gäller:

$sin^2\alpha+cos^2\alpha=1$

Så ett byte att tänka på är en sådan som gör om cosinus till sinus eller vice versa.

Vi börjar med att separera integralen, så att vi får två integraler, en för cosinus-delen och en för sinus-delen:

Vi använder sedan det trigonometriska faktum att sin(x) = cos(x-pi/2) för att skriva om den innersta sinusfunktionen i sinus-integralen:

Vi genomför variabelbytet u = x-pi/2. Integralen får då de nya gränserna -pi/2 till 0:

Vi observerar dock att cos(u) är en jämn funktion, varför vi kan ändra gränserna och få samma integral från 0 till pi/2.

Om vi nu slår samman våra två integraler, och betraktar dem som en gemensam integral över x, då får vi den välkända trigonometriska ettan:

Integralens värde blir då förstås differensen av ändpunkterna, det vill säga pi/2.

Etikett: integral