Mattebloggen

På ett papper finns en bild på en svart kvadrat. Du har tillgång till 7 kvadratformade brickor av samma storlek som den ritade kvadraten. Hur ska du göra för att täcka över kvadraten med brickorna så att inga brickor ligger på varandra och varje bricka täcker åtminstone en liten del av kvadraten (åtminstone en punkt inuti)?

Det kluriga ligger i att lista ut att man kan vrida på brickorna innan man lägger dem på kvadraten. Den lösningen kom de regelbundna lösarna Johan och Ove på, men också niorna Amanda, Elin, Emelie, Adam, Michaela och Hampus från Häggviksskolan i Stockholm. Författaren tackar Adam Jonsson, deras lärare, för hans engagemang!

Här är de inskickade lösningarna, som förstås är egentligen likadana. Notera dock att alla lösningar är fel för att kvadraten inte är svart ;)

Lösning:

På ett papper finns en bild på en svart kvadrat. Du har tillgång till 7 kvadratformade brickor av samma storlek som den ritade kvadraten. Hur ska du göra för att täcka över kvadraten  med brickorna så att inga brickor ligger på varandra och varje bricka täcker åtminstone en liten del av kvadraten (åtminstone en punkt inuti)?

Från början har vi en kvartscirkel med radie 1 (cm om man så vill). Gränserna för kvartscirkeln utgör diametrar för två mindre cirklar, deras halvor syns på bilden.

i) Hur förhåller sig areorna A och B?

ii) Vad är areorna A och B lika med?

Lösning:

(i) Notera att areorna A och C tillsammans utgör halva lilla cirkeln, det vill säga halva cirkeln med diameter 1. Den har area pi*((½)^2)/2. Samma gäller A och D, A+D=pi*((½)^2)/2=pi/8.

Å andra sidan utgör A+B+C+D en kvarts stor cirkel, således A+B+C+D=pi*(1^2)/4=pi/4. Vi ser att arean för den stora kvartscirkeln är dubbelt så stor som areorna för de små halvorna.

Således har vi A+B+C+D=(A+C)+(A+B), och subtraher vi A, B och C på båda sidor av likheten, så får vi A=B. Notera att vi nu inte har bestämt själva areorna, utan bara hur A och B förhåller sig.

(ii) Följande är min arbetskamrats Albins lösning:

Om man ritar ut den små (röda) cirklarna, syns det tydligare vad som händer. Den gröna punkten är skärningspunkten mellan tangentlinjer (svarta) till cirklarna, som då måste bilda 90° vid skärningen. Då är vinkeln mellan de två röda cirklarna också 90°.

Då vet vi att också de blåa tangentlinjerna skär varandra i vinkeln 90°. Det kan också ses av symmstriskäl. Från den gröna och från den blåa punktens perspektiv måste allting vara symmetriskt. Alltså bildas en kvadrat rektangel i mitten av bilden (en kvadrat egentligen), eftersom igen, av symmetriskäl så måste återstående två vinklarna vara lika och då måste de vara 90° också.

Nu finns olika sätt att bestämma arean A och jag gör det med liknande metod som i (i).

Här har vi att A+x=pi/16, en kvart av en cirkel med radie ½. A+x+x=1/4, arean av kvadraten. Alltså är x=1/4-pi/16. Och då måste A=pi/16-(1/4-pi/16)=pi/8-1/4.

Svar: 

Jag hoppas att ni flitigt har försökt lösa de här uppgifterna. Nu tänker jag nämligen berätta lösningen till uppgift 3. Dessutom följer en förklaring på hur man tänker. Uppgiften är alltså:

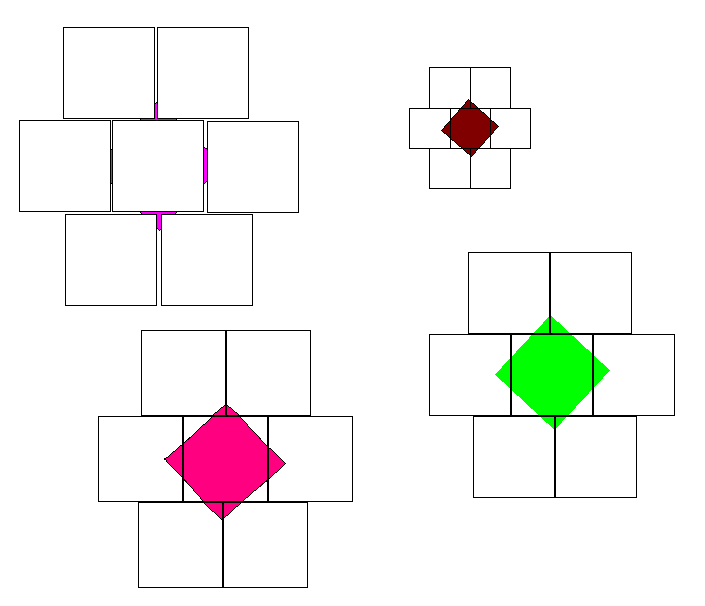
Visa att en kvadrat kan delas upp i n stycken mindre kvadrater för alla n>5. 

Med ”att dela upp” menas att vi klipper en kvadrat så att alla erhållna delar också är kvadrater och det blir inga bitar över. Vi ska hitta på en sådan klippning för alla möjliga antal bitar, från och med 6.

Det känns lite omöljigt, hur ska vi kunna ge en lösning för alla tal som är större än eller lika med 6? Det tar ju oändligt lång tid att presentera! Men, uppgiften säger ”visa att”, det vill säga ”visa att det går” och det frågas inte hur, vilket är två olika saker. Det är skillnad på ”visa att ekvationen har en lösning” och ”bestäm en lösning för ekvationen”. På samma sätt som det är skillnad på ”visa att dinosaurierna levde på Jorden under hundra miljoner år” och ”hitta hundra miljoner årtal under vilka dinosaurierna levde”. Det kan vara subtil olikhet mellan de paren av påståenden, men det är bara så att det senare svaret skulle ge oss det tidigare men inte tvärtom. Man kanske vet att dinosaurierna levde under en viss period, men är osäker på under vilka årtal de säkerligen levde. Men ger någon oss årtal så är det klart att dinosaurierna levde i minst hundra miljoner år.

Men åter till problemet, hur ska man börja lösa det? Tvärtemot vad jag precis skrev om, ska man försöka konstruera lösningarna explicit för olika tal. Vilka n lyckas vi med? Det är en viktig metod i problemlösning, som säger att vi ska starta med små fall, trots att vi har godtyckligt stora framför oss. Små fall kommer ge oss en känsla för hur problemet funkar.

Ok, i hur många kvadrater kan du dela upp en stor kvadrat? Jag kan i 4! Visst, det ingick inte i problemet att lösa det för 4, men jag kan ändå:

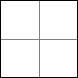
Det går upprepa samma idé och få 9, 16, (och så vidare) kvadrater:  

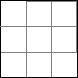
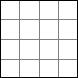
Detta ger oss inte så mycket, bara alla kvadrattal, men vi har oändligt många kvar. Vad händer om vi änvänder ”samma konstruktion” som i fallet 4, fast på ett annat sätt? Jag menar så här:

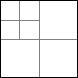
Och vi kan givetvis fortsätta på samma sätt, splittrande en av kvadraterna i fyra små. Vi kan få 7 kvadrater som på bilden ovan och sedan också 10, 13 osv:

Det spelar ingen roll för oss vilken av de befintliga kvaraterna vi delar in i fyra nya. Det viktigaste är att antalet ökar med 3 hela tiden.

Vi har alltså fått svaret för 7, 10, 13, 16, 19, … Oändligt många svar, med det är ändå foftarande oändligt många kvar! Men ni kanske kan gissa att talen 6, 9, 12, 15, …. och talen 8, 11, 14, 17, …. kan fixas på samma sätt så fort vi hittar på någon lösning för 6 respektive 8 kvadrater. Notera då att alla tal större än 6 kommer vara fixade då.

Okej, försök att klura ut 6 eller 8 kvadrater själv innan du tittar nedan. Ett tips är att ha en motsatt taktik: i stället för att lägga till kvadrater till en befintlig konstruktion, försök att ta bort lite kvadrater.

För att få 6 kvarater tar jag bort lite från min konstruktion på 9 kvadrater:

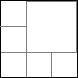
På liknande sätt gör vi 8 kvadrater från 16:

Då är vi klara! Vi kan få alla konstruktioner från konstruktionerna med 6, 7 och 8 kvadrater genom att dela upp en kvadrat i fyra och därmed lägga till 3 till antalet.

Vad har då detta med induktion att göra?

Denna lösning, som går ut på metoden ”stegvis konstruering”, kan även anpassas till induktionsmodellen. I det här problemet består inte induktionssteget av ett enda ”steg”, från talet n till talet n+1, utan av tre fall som i och för sig löses på samma sätt (fallen är olika kongruensklasser modulo 3). Basen bestär också av olika fall. 

Uppgiften är löst, vi förstår hur lösningen funkar, det är nu vi kan baka in den i induktionsmodellen:

Bas:

n=6, n=7 och n=8:

Induktionssteg:

Induktionsantagandet är att det går att dela upp en stor kvadrat i n stycken mindre. Vi visar att det då går att dela upp i n+3 stycken mindre. Beviset är: skär en av gamla kvadraterna i fyra nya.

Slutsats:

Enligt inuktionsaxiomen och alla basfall modulo 3 visade kan vi dra slutsatsen att påståendet gäller för alla n>5.

Detta kanske inte var det bästa exemplet på att induktion kan vara bra. Lösningen ser mycket naturligare ut i den mindre formella beskrivningen. Men å andra sidan blir den mycket kortare och mer elegant formulerat i induktionstermer.