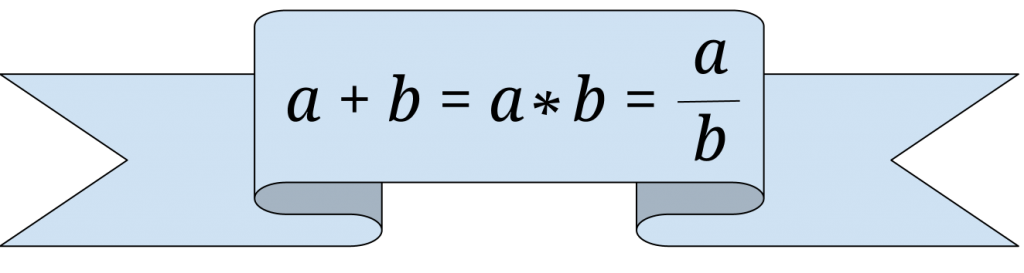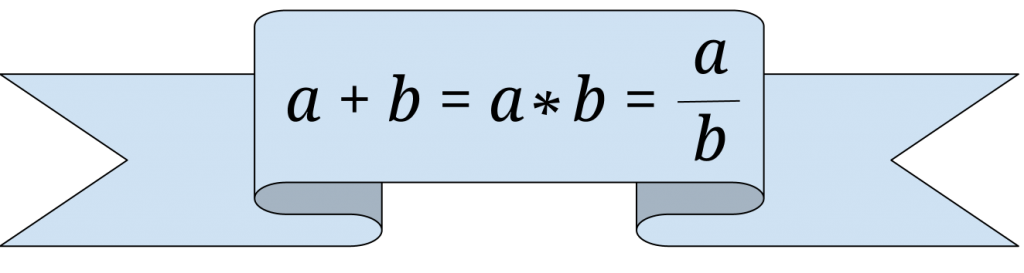Antag att sådana två magiska tal a och b existerar.
Om a*b = a/b, så måste a*b*b = a. Det betyder att a = 0 eller b*b = 1.
Men a kan inte vara lika med 0, för då vore 0+b = 0*b = 0, det vill säga b = 0 också. Men kvoten 0/0 är inte lika med 0.
Därför är b*b = 1, således b = 1 eller b = -1.
Men om b vore lika med 1, så skulle a+1 = a*1 = a, vilken inte kan vara sant.
Så b = -1 och vi har att a-1 = a*(-1) = a/(-1). Om a-1 = -a, så gäller 2a = 1, det vill säga a = 1/2.
a = 1/2, b = -1 är en fungerande lösning, och det är även den enda lösningen.