Multiplikationer i en tabell
På hur många sätt kan man fylla en 6×6-tabell med 1:or och -1:or så att produkten av talen i varje rad och i varje kolumn blir lika med 1? (Det är alltså tolv stycken produkter som ska bli lika med 1.)
Utökad produkt
Utökad produkt
[kkratings]
Det finns tre tal givna. Om alla tal utökas med 1, så kommer deras produkt också utökas med 1. Om alla tal utökas med 2, så kommer deras produkt också utökas med 2.
Hur mycker ökar produkten med om alla talen ökar med 3?
Två magiska tal
Två magiska tal
[kkratings]
Finns det två tal, sådana att deras summa, produkt, samt kvot sammanfaller?
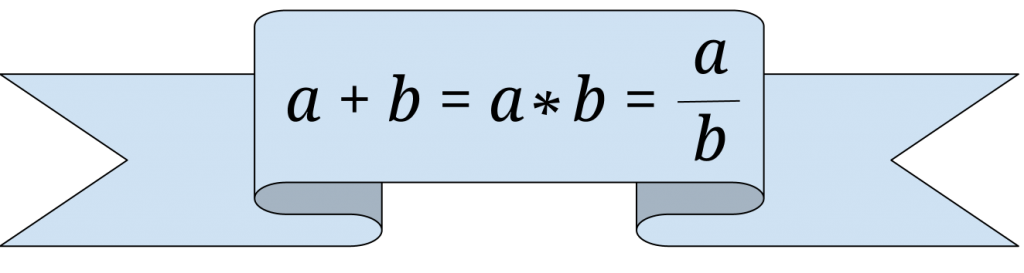
Adventspyssel 19
Jalusimetoden
Min elev Erik har lärt mig hur man multiplicerade stora tal på medeltiden. Uppställningen påminner om hur vi gör nu, men talens enskilda siffror multipliceras i en tabell.
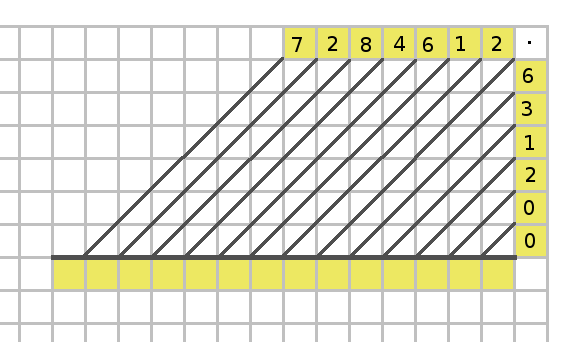
Skriv upp två tal som du vill multiplicera, ena som vanligt från vänster till höger, det andra uppifrån och ned, och gör diagonala streck som på bilden. Produkten ska skrivas in i rutorna längst ner.
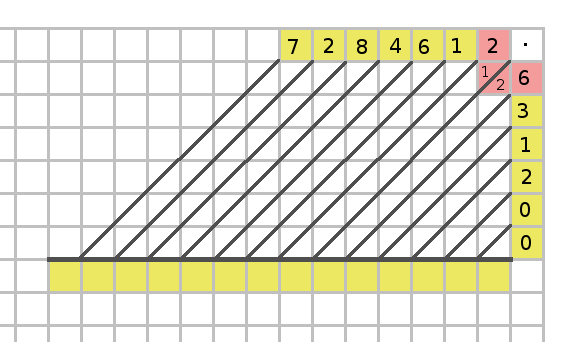
Varje siffra i första talet ska multipliceras med varje siffra i det andra talet. Resultatet skrivs in i rutan som motsvarar kolonnen för första siffran och raden för andra.
Om resultatet är till exempel 2*3=6 så skrivs 0 in i vänstra halvan av rutan och 6 i högra. Man behöver egentligen inte skriva in nollor.
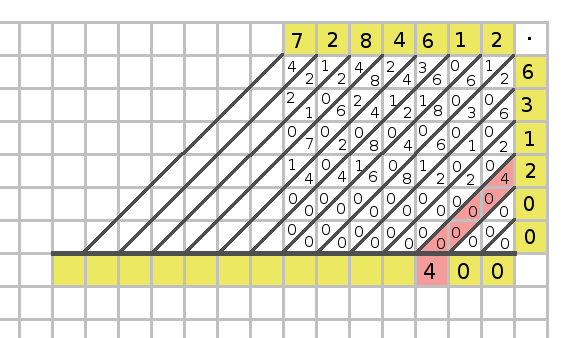
Nu är alla multiplikationer gjorda och det är dags att addera!
Det är därför vi hade sneda linjer, det är längs med dem vi ska addera! Till exempel blir den tredje sneda summan lika med 4.
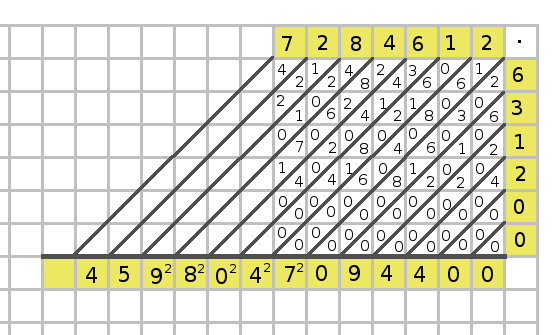
Vi fortsätter att addera från höger till vänster och ibland blir det minnessiffror (i det här exemplet råkade alla minnessiffror vara lika med 2).
Min elev tyckte att det här var det bästa sättet att multiplicera och att han framöver bara skulle utföra sådana här multiplikation!
Vilken multiplikationssätt tycker du bäst om?