Ett lejon springer runt på en rund cirkusarena, som har radien 10 m. Lejonets bana består av raka streck och i slutändan springer han 30 km. Visa att summan av alla vinklar, som lejonet svängde under springturen, är minst 2998 radianer.
Säg att  är sträckorna som lejonet springer på, medan
är sträckorna som lejonet springer på, medan 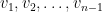 är vinklarna som han svänger på. Betrakta lejonets bana på följande sätt.
är vinklarna som han svänger på. Betrakta lejonets bana på följande sätt.
Låt han springa sträckan 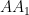 med längden
med längden 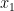 . Rotera då arenan kring lejonet, det vill säga punkten
. Rotera då arenan kring lejonet, det vill säga punkten 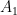 , med vinkeln
, med vinkeln 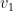 , på så sätt att sträckan
, på så sätt att sträckan  blir en fortsättning på sträckan
blir en fortsättning på sträckan 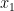 . Efter att lejonet sprunget sträckan
. Efter att lejonet sprunget sträckan  , rotera arenan med vinkeln
, rotera arenan med vinkeln  , så att
, så att 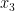 utgör fortsättningen utav
utgör fortsättningen utav  , och så vidare. I så fall springer lejonet rakt fram hela tiden och totalt sett springer han sträckan
, och så vidare. I så fall springer lejonet rakt fram hela tiden och totalt sett springer han sträckan 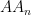 , som är 30000 meter lång.
, som är 30000 meter lång.
Hur arenans mittpunkt 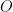 rört sig under tiden? Först roterar
rört sig under tiden? Först roterar 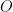 kring punkten
kring punkten 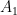 med vinkeln
med vinkeln 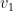 , sedan kring
, sedan kring  med vinkeln
med vinkeln  och så fortsätter det på samma sätt.
och så fortsätter det på samma sätt. 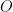 är aldrig längre bort än 10 meter från rotationens centrum, eftersom rotationens centrum är lejonet, som alltid befinner sig inuti arenan. Därför kommer
är aldrig längre bort än 10 meter från rotationens centrum, eftersom rotationens centrum är lejonet, som alltid befinner sig inuti arenan. Därför kommer 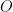 som mest flyttast
som mest flyttast 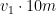 vid första rotationen,
vid första rotationen, 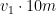 vid andra och så vidare (om
vid andra och så vidare (om  mäts i radianer). Så
mäts i radianer). Så 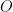 kommer maximalt att flyttas
kommer maximalt att flyttas  . Alltså:
. Alltså:
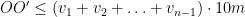 .
.
Startarenan ger oss  , slutarenan ger
, slutarenan ger  .
.
Och då, eftersom 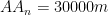 , så är
, så är 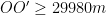 . Således har vi att:
. Således har vi att:
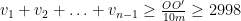 radianer.
radianer.

