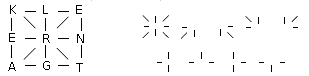Skicka in lösningsförslag genom att klicka på länken under uppgifterna senast måndagen den 14 mars. Glöm inte att kolla reglerna och aktuella poängställningen.
Rebusen (1 poäng). Försök att läsa av ordet genom att använda nyckeln:
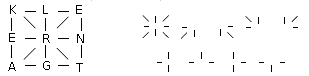
Schackcirkeln (3 poäng). Det finns ett vanligt schackbräde med storleken 8×8. Hur stor radie har den största cirkeln man kan rita, som bara går igenom svarta rutor (det vill säga cirkelns rand finns aldrig i de vita rutornas inre)? Visa varför det inte går att hitta en större sådan cirkel.
Visa lösningar
Rebusen (Pierres lösning):
Ordet är rektangel, med hjälp av strecken kan man lösa det.
Schackcirkeln (Roberts lösning): Motsägelsebevis att största möjliga radie är √(1,52+0,52):
För att cirkeln skall vara stor måste den gå genom mer än en svart ruta. Då måste den passera genom hörn. Från och med nu koncentrerar jag mig på vilka hörn den kan gå genom. När cirkelns rand går in genom ett hörn till en ruta kan det antingen gå ut genom det diagonalt motsatta eller ett närliggande hörn.
Då använder jag följande konstateranden:
1: Om randen gick genom diagonalt motsatta i föregående ruta kan det inte igen gå genom diagonalt motsatta. Då skulle de tre hörnen vara kolinjära och radien oändlig.
2: Om den går genom närliggande hörn två gånger i rad blir diametern √(1,52+0,52).
3: Bästa resultat blir om det alternerar: varannan i motstående diagonalt och varannan i närliggande. Då blir radien enligt ovan.