Feta streck
[kkratings]
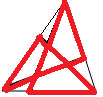
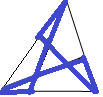
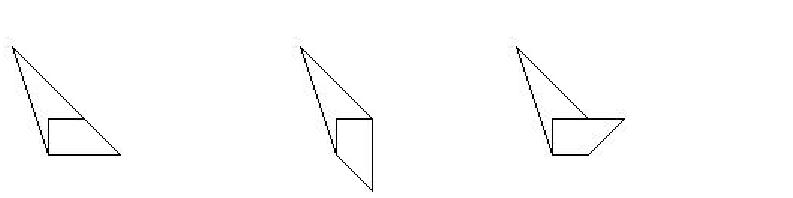
Triangeln på bilden är uppdelad i fyra trianglar och tre fyrhörningar med de feta strecken.
Fyrhörningarnas omkretser tillsammans är 25 cm. Summan av omkretsarna för de fyra trianglarna är 20 cm. Den stora ursprungliga triangelns omkrets är 19 cm. Bestäm summan av längderna av de feta strecken.
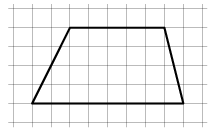
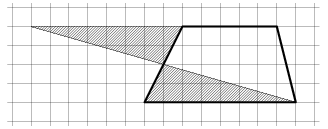
Trapets till en triangel
Trapets till en triangel
En lektion för små barn om trianglar
Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.
Notera att barnen redan har haft två lektioner om vinklar och olika vinkeltyper.
Trianglar
Det är dags att sätta ihop punkter, sträckor och vinklar till trianglar!

Sammanbinda punkter
Uppgiften är att kopiera av punkter på bilden till sitt eget papper och sedan sammanbinda dem till en triangel. De yngre barnen får ett lika stort papper som originalet, men de äldre får en annan storlek och därmed implicit får träna skala.
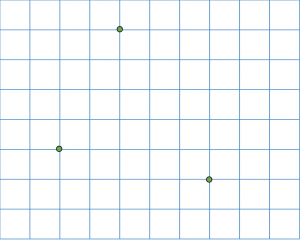
Hur många hörn har en triangel? Hur många sidor?
Hur många spetsiga vinklar kan du hitta i din triangel? Hur många trubbiga? Är det någon som har en triangel med en rät vinkel?
Efter att alla är klara med övningen kan barnen få extraövning (eller så blir det läxa): sammanbinda alla tripplar av punkter, som är av samma färg.
Den här bilden:
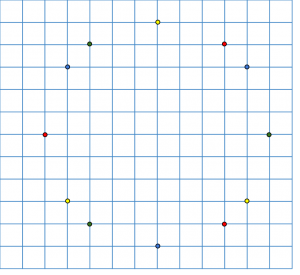
Blir till en tolvuddig stjärna:
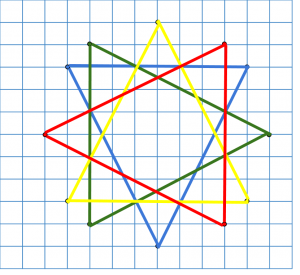
Rita och klipp ut en egen triangel
Barnen får välja färg på pappret och ett uppdrag av mig: rita en spetsvinklig, trubbvinklig eller en rätvinklig triangel. Sedan skall trianglar klippas ut och vi ordnar dem efter storleken på den största vinkeln (först den mest trubbvinkliga triangeln, sedan andra trubbvinklig, sedan rätvinkliga etc.).
Efter det får barnen låna varandras pappersrester för att klippa ut andra trianglar och bygga ihop ett torn (som bara består av trianglar). Tillsammans tillverkar vi ”triangellandet”:

Kanske lägger jag ihop Sergels Torg – mönstret under tiden. Eller så klipper jag ut svarta och vita trianglar och barnen får arrangera dem till ”Sergels Torg”.

Triangelolikheten
Nu skall trianglar byggas av pinnar. Men det är inte alltid det går! Får man tre pinnar med längder 2cm, 3cm respektive 6cm, så går de inte sätta ihop till en triangel. Anledningen är triangelolikheten.
Barnen får en massa pinnar och skall hitta tre stycken som de kan sätta ihop till en triangel (med häftmassa till exempel). De äldre barnen ska försöka förklara när det går att bygga en triangel och när det inte går.
Vägar
Apropå triangelolikheten kan vi prata om den kortaste vägen och det kortaste avståndet med 7- och 10-åringarna. Hur kan man t.ex. avgöra om ens handled eller fotled är smalare (t.ex. med snöre)? Med samma hjälpmedel kan man avgöra vilket har större omkrets: en cirkel eller en liksidig triangel, inskriven i cirkeln?
Vilken väg från dörren till fönstret är kortast (notera att bord kan vara i vägen för den raka sträckan)?

Bygga med en magnetisk struktur
Vi avslutar med att pyssla med en magnetisk byggsats, där bitarna är magnetiska pinnar och kulor, som binds ihop väldigt starkt med varandra. Vilka former på trianglar går att bygga med hjälp av byggsatsen? Går det att bygga 3D-strukturer som består av trianglar och i så fall vilka? (T.ex. en tetraeder eller en ikosaeder går att bygga.) För de äldsta barnen berättar jag om de platonska kropparna som finns och vi försöker bygga dem alla.

Notera att jag antagligen inte hinner med allt ovanstående på alla lektioner. Ibland fastnar barnen på en sak, ibland blir uppgiften för svår. Men det mesta kommer ändå med på lektionerna.
Liksidiga trianglar?
Rekommenderad från: 15 år
[kkratings]
Mattebloggen har en inofficiell tävling i att lösa matematikproblem. Skicka in din lösning med motivering till valentina.chapovalova@gmail.com, så har du chansen att vara med på topplistan. Har du någon fråga om veckans problem, posta den i kommentarerna eller maila mig. Lycka till!
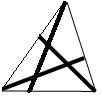
I en triangel ABC så är mitten av sidan AB markerad med punkten M. Även höjderna AH och BL är utritade. Det visade sig att triangeln MHL blev liksidig. Måste det vara så att även triangeln ABC är liksidig?
Om ja, ge ett bevis för varför den måste vara det. Om nej, visa hur ett motexempel konstrueras.
Två fyrkanter
Rekommenderad från: 12 år
[kkratings]
Rita två fyrkanter, som tillsammans kan läggas ihop till
(i) En triangel, men också en femkant
(ii) Både en triangel, en fyrkant och en femkant.
Med ”läggas ihop” menas att fyrkanterna inte får överlappa varandra, inte heller får det bildas hål.
© 2009-2025 Mattebloggen