Den senaste träffen på Katedralskolan genomförde vi en liten tävling bland deltagarna.
Varje deltagare fick 5 stycken problem att lösa på kort tid. Dock behövde inte problemen lösas fullständigt, utan det viktiga var att uppnå ett resultat. Men jämna mellanrum samlade jag in resultaten på varje problem. Sedan får det sämsta resultatet 1 poäng, nästa resultat får 3 poäng och så vidare.
Till exempel, när det hade gått 5 minuter av tävlingstiden så lämnade deltagarna in sina svar (tillsammans med exempel) på problem 1. Säg att deltagarna lyckas med svaren 20, 22, 20 och en lösning är felaktig. I det här fallet är det bra att ha så litet svar som möjligt. Personen med svaret 22 får då 1 poäng, personerna med svaren 20 får då 4 poäng var (de delar jämnt på 3- och 5-poängaren). Personen utan giltig lösning får inga poäng.
Testa själv att uppnå så bra resultat som möjligt på 25 minuter. Läs igenom problemen först och starta sedan klockan. Posta gärna dina bästa resultat i kommentarerna sedan, så kan vi se vem som vinner ”tävlingen” här på bloggen.
Fem minuter per problem
1. Placera springare på schackbrädet 8×8 för att de ska angripa samtliga lediga rutor. Ju få springare desto bättre.
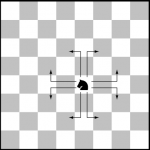
2. Skriv ner på en rad några på varandra följande positiva heltal som har siffersummor ej jämnt delbara med 8. Ett exempel: 18, 19, 20. Ju fler tal desto bättre.
3. Fyll i en tabell av format 3×5 med olika positiva heltal. Summan i ett vilket som helst par grannrutor skall inte vara jämnt delbart med 3. Som grannar räknas rutor med en gemensam sida eller ett gemensamt hörn. Ju mindre det största talet i tabellen blir desto bättre.
4. Hitta ett tal med samma siffersumma som siffersumman hos 1992 och samma sifferprodukt som sifferprodukten hos 1992. Ju större talet är desto bättre.
5. Det finns tillräckligt många kort med talen 9, 49, 169, 289, 729 och 625. Plocka ut ett antal kort med summan 2004. Ju färre kort desto bättre.
