Papper (3 poäng).
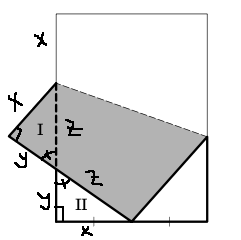
Man tog ett rektangulärt papper och vikte ihop det så att ena hörnet hamnade i mitten på kortsidan (se bilden). Det visade sig att trianglarna I och II var kongruenta.
Hur lång var papprets långsida om kortsidan var 8 cm lång?
Brickor (7 poäng). En kvadrat med storlek 6×6 ska övertäckas med 12 brickor (utan hål och överlapp). Vissa brickor (k stycken) får vara vara ”hörn” bestående av tre rutor och resten (12-k brickor) måste vara tre rutor stora rektanglar.
För vilka k är uppdelningen möjlig?
Visa lösningar
Papper (Thomas lösning):
På grund av kongruensen är sidorna markerade x lika långa, och samma sak gäller för de markerade y, och z. Vi ser att höjden h = x + y + z och x = 8/2 = 4, och y + z = 8 eftersom kortsidorna hade längd 8, så att h = 4 + 8 = 12 cm.
Brickor (Skäggets lösning):
Med två hörn kan vi bilda en 2×3-rektangel, och vi kan bilda en likadan rektangel med två 1×3-rektanglar. Hela brädet går trivialt att fylla med 2×3-rektanglar, och således kan vi för jämna k bilda k/2 sådana rektanglar med bara hörn och låta resten vara 1×3-rektanglar. Således kan brädet fyllas för jämna k.
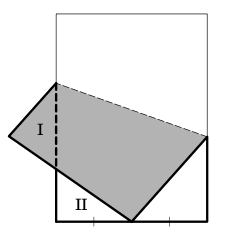
För udda k större än 3, betrakta Bild 1 som visar en täckning med 5 hörn, en 1×3-rektangel och tre 2×3-rektanglar. Genom att välja hur de sistnämnda rektanglarna byggs upp (antingen med två hörn eller två 1×3-rektanglar) kan vi alltså täcka brädet för k = 5, 7, 9 och 11.
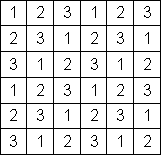
För k = 1 kan vi utan inskränkning anta att hörnet är sådant att det passar in i det övre-vänstra hörnet på brädet. Låt oss då numrera rutorna som i Bild 2. Vårt hörn kommer inte kunna täcka en av varje siffra, men hur man än placerar ut 1×3-rektanglar på brädet täcker de exakt en av varje siffra. På slutet ska lika många av varje siffra ha täckts, men det är omöjligt, eftersom antalet av de siffror som täckts av hörnet alltid kommer vara fler. Alltså existerar ingen lösning för k = 1.
För k = 3, låt oss dela in hörnen i två kategorier: De som passar in i övre-vänstra och undre-högra hörnen och de som passar in i de övriga två hörnen. Antag att det finns en övertäckning, och att våra tre hörn inte alla är av samma kategori. Då finns det två ur den ena kategorin och en ur den andra. Vi kan utan inskränkning anta att det finns exakt en ur den första kategorin, och vidare utan inskränkning anta att den passar in i övre-vänstra hörnet. Med samma resonemang som för k = 1 får vi nu att detta hörn inte täcker alla tre siffror enligt vår numrering av brädet, medans alla hörn ur den andra kategorin, samt alla 1×3-rektanglar, täcker exakt en av varje. Således finns det ingen lösning för k = 3 om vi har hörn ur båda kategorier.
Så antag att det finns en lösning för k = 3 där alla tre hörn är av samma kategori. Vi vet att de tre hörnen måste täcka lika många av varje siffra enligt vår numrering, det vill säga tre av varje. Låt hörn av typ 1 vara sådana som passar in i övre-vänstra hörnet av brädet och de andra vara av typ 2. Hörn av typ 1 kan täcka punkter (1, 2, 2) eller (2, 3, 3) eller (3, 1, 1) medans hörn av typ 2 kan täcka (3, 2, 2) eller (1, 3, 3) eller (2, 1, 1). Vi kan väldigt lätt verifiera att ingen kombination som har något hörn ur båda kategorier kan täcka exakt tre av varje siffra, eftersom varje par med ett hörn av varje typ ger antingen fyra av någon siffra, inget av en siffra, eller två av varje siffra, och det finns inget hörn som kan utvidga detta till att täcka tre av varje siffra. Således måste varje hörn vara av samma typ om någon lösning finns. Vi kan utan inskränkning anta att de är av typ 1.
Vi visar nu med induktion att ingen rektangel på formen 6xN (sex rutor bred) kan täckas med exakt tre hörn av samma typ. Basfallet med en 6×1-rektangel är trivialt eftersom hörnen inte ens får plats. Antag nu att det är omöjligt för alla rektanglar upp till 6xN, så ska vi visa att det inte finns någon lösning för 6xN heller.
Det nedre-högra hörnet i en 6xN-rektangel måste uppenbart täckas av en rektangel och inget hörn. Vi kan utan inskränkning anta att den ligger horisontellt (annars kan vi spegla brädet så att den gör det, eftersom det hörn vi valt är symmetriskt längs den diagonalen).
Det finns nu tre möjliga fall:
1) Till vänster om vår utlagda rektangel har vi en till horisontell rektangel. Då har vi täckt hela understa raden och ska därmed fylla en (N-1)x6-rektangel med tre hörn av samma typ. Det har vi antagit är omöjligt.
2) Till vänster om vår utlagda rektangel har vi en vertikal rektangel. Då har vi ett utrymme till vänster om den rektangeln, av måtten 2×3, som uppenbart bara kan fyllas med två vertikala rektanglar. Då får vi tre vertikala rektanglar bredvid varandra. Antag nu att resten av brädet går att fylla.. Då existerar det nödvändigtvis även en lösning där vi istället för tre vertikala rektanglar har tre horisontella (de täcker ju samma 3×3-kvadrat). Men om vi bortser från den understa raden har vi då även en lösning för en (N-1)x6-rektangel, vilket vi antagit är omöjligt.
3) Till vänster om vår utlagda rektangel har vi ett hörn. Då har vi ett 2×2-utrymme till vänster om hörnet som måste fyllas på något vis. Det går uppenbart bara med två vertikala rektanglar. Nu har vi en trappa från höger till vänster, med trappsteg av längd 2 och höjd 1. På det understa trappsteget har vi ett 2×1-uttrymme som bara kan fyllas med två vertikala rektanglar. Detta lämnar ett liknande utrymme på mittentrappsteget som även det bara kan fyllas med två vertikala rektanglar. Slutligen måste vi även placera två vertikala rektanglar i det lediga 2×2-utrymmet som bildas på översta trappsteget. Nu har vi en likadan trappa som tidigare, fast tre rutor högre upp. Om resten går att fylla med två rektanglar, då skulle vi kunnat flytta ner den resterande biten tre steg och fyllt en (N-3)x6-rektangel. Men det är ju omöjligt från induktionsantagandet.
Våra tre möjliga fall visade sig samtliga vara omöjliga, och alltså existerar det ingen lösning för k = 3. Sammanfattningsvis har vi alltså hittat lösningar för alla k utom 1 och 3, och för dessa existerar det inga lösningar.