Triangellandet har formen av en liksidig triangel. En inre gräns delar landet i två stater, som har lika stor area. Beskriv hur gränsen ser ut (formen och positionen) om den har den minsta möjliga längden.
Låt oss anta för enkelhets skull att triangelns sida är 1. Då är landets area 
.
Det finns två fall: antingen går gränsen från ett hörn till den motsatta sidan eller mellan två sidor.
Fall 1.
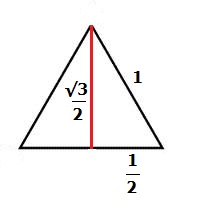
Om en sträcka ska gå från ett hörn till den motsatta sidan i en triangel och dela den i två delar med lika stora areor, så måste sträckan vara medianen (och alltså även höjden). I en liksidig triangel är höjden lika med 
.
Fall 2.
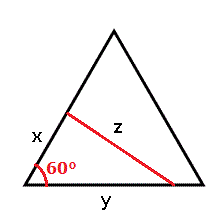
Vi tittar på den lilla triangeldelen som bildas, den ska ha arean 
. Den har å andra sidan vinkel 60 grader och areaformeln säger:
Arean = 
.
Således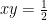 
och 
, oavsett formen på triangeln.
Vi försöker minimera sidan 
, till vår hjälp har vi cosinussatsen:
Vi skall minimera , alltså 
och således även 
För att hela uttrycket ska bli så litet som möjligt, bör kvadrattermen vara lika med 0. Alltså har vi:
Då kan vi räkna ut längden på den minsta gränsen i det här fallet:
Det blev en mindre sträcka än i det första fallet, således är svaret 
.
Stämmer fall 2 i lösningen verkligen? När jag försöker maximera den sidan så sammanfaller det med fall 1, dvs höjden är den sträcka som är kortast.
Oj, ursäkta! Formeln är fel och då fallerar lösningen. Svaret är istället
och jag skriver en ny lösning snarast möjligt.
Så måste det naturligtvis bli. En likformig (dvs liksidig) triangel som den med sida 1 fast istället med sida sqrt(2)/2. Då blir ju arean hälften så stor.