Att rita tre kvadrater
[kkratings]
Går att rita följande figur utan att lyfta pennan från pappret? Det är inte tillåtet att dra samma sträcka flera gånger.
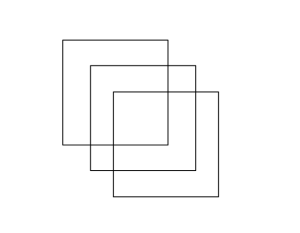
Roligare matematik
[kkratings]
Går att rita följande figur utan att lyfta pennan från pappret? Det är inte tillåtet att dra samma sträcka flera gånger.

© 2009-2025 Mattebloggen
Jag antar att den triviala lösningen där man drar samma streck mer än en gång inte är tillåten :P
/poke
Ja, självklart! Det borde jag förtydliga.
Ja men om linjen inte får korsa sig själv då? Då blir det lite marigare. Men det går!
Mats, intressant fråga! Japp, det går. Man kan till och med lösa probemet genom att försöka ”separera” korsningar.
Nu vore det roligt att ta reda på om alla bilder som går att rita utan att lyfta pennan och dra streck flera gångar går att rita så att vi aldrig korsar gamla linjer (bara nuddar). Jag tror svaret är ja, tänker ut beviset lite senare.
Det visar sig att svaret är nej (det går inte alltid) för figurer som startar och slutar i olika punkter. För ett enkelt motexempel tänk bokstaven lilla alfa, den måste korsa sig själv.
Svaret är dock ja för figurer som startar och slutar i samma punkt, men beviset är lite mer komplicerat, så vi kan ta det muntligt när vi träffas, Mats. Dessutom tycker jag att det blev så bra problem att man eventuellt skulle kunna skicka in det till en tävling och därför vill jag inte skriva lösningen här :)
Varför fungerar inte lilla alfa? Det verkar fungera för mig.
Haha, ja det gör det ju! Glömde att testa det andra sättet :)
Jamed då fungerar det lika bra för sådana figurer som startat och slutar i olika puntker också.
Det var en rolig uppgift, jag tror jag har en lösning nu också även om det är snyggare om man inte har några noder av udda paritet.
Räcker sammanhängande + inga noder av udda grad för att det ska existera en ”pennstreckslösning”?
Japp, sammanhängade + två av udda grad implicerar eulerstig = pennstreckslösning, sammanhängande + noll av udda grad implicerar eulercykel = pennstreckslösning (som måste börja och sluta i samma punkt).