Geometri – Sida 3 – Mattebloggen

Problem vecka 18

Cirkelkonstruktion (2 poäng).
Du har en passare, som du kan rita cirklar med (så länge du känner till cirkelns mittpunkt och dess radie) samt en ograderad linjal, som du inte kan mäta något med, men som du kan rita en linje med genom två valfria punkter.

Du har fått ett papper där en cirkel c är ritad (och dess mittpunkt är markerad) och där en punkt A utanför cirkeln är markerad.

Hur kan du med hjälp av dina verktyg rita en ny cirkel, som har A som mittpunkt och som precis tangerar den redan ritade cirkeln c? Bevisa att din konstruktion ger korrekt resultat.

Cosinussumman (5 poäng).
Visa att ifall summan av cosinusar på vinklarna hos en fyrhörning är lika med 0, så måste fyrhörningen antingen vara cyklisk, en parallellogram eller ett parallelltrapets.

Visa lösningar

Cirkelkonstruktion (Davids lösning):
Låt B vara mittpunkten i cirkeln c. Drag sträckan AB. Låt X vara punkten där AB skär c. Rita en cirkel med mittpunkt i A och som går genom X. Jag vill visa att denna cirkel tangerar c. De har ju en gemensam punkt X, så jag vill visa att de inte har någon annan gemensam punkt.

Antag att de har en annan gemensam punkt Y. Då finns det två sätt att gå från A till B: via X (vägens längd är |AX|+|XB|) eller via Y (vägens längd är |AY|+|YB|). AX och AY är radier i vår konstruerade cirkel, alltså |AX|=|AY|. XB och YB är radier i c, alltså |XB|=|YB|. Alltså |AX|+|XB|=|AY|+|YB|. Men när vi går via X följer vi en rät linje enligt vår konstruktion, så ingen annan väg från A till B kan vara lika kort. Vilket motsäger att vägen via Y är lika kort. En motsägelse som visar att vår cirkel och c har en och endast en gemensam punkt, alltså tangerar de varandra.

Cosinussumman (Skäggets lösning):
Vi börjar med att konstatera att ett parallellogram är ett specialfall av en parallelltrapets, så vi visar bara att en fyrhörning är antingen cyklisk eller en parallelltraptes om summan av cosinus av vinklarna är 0.

Låt oss kalla vinklarna i vår fyrhörning för A, B, C och D (med ordningen än så länge godtycklig).

Vi vet att summan av vinklarna i en fyrhörning är 360 grader, och vi kommer använda följande identitet för cosinus:

$cos X + cos Y = 2\ cos(\frac{X+Y}{2})\cdot cos(\frac{X-Y}{2})$

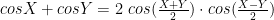
Vi antar nu att summan av cosinus av alla vinklar är noll, det vill säga:

$cos A + cos B + cos C + cos D = 0$

$\iff 2\ cos(\frac{A+B}{2})\cdot cos(\frac{A-B}{2})+2\ cos(\frac{C+D}{2})\cdot cos(\frac{C-D}{2})=0$

$\iff cos(\frac{A+B}{2})\cdot cos(\frac{A-B}{2})=-cos(\frac{C+D}{2})\cdot cos(\frac{C-D}{2})=0$

Vi vet att D = 360 – A – B – C, samt att cos (180 – X) = – cos X. Detta ger oss:

$cos(\frac{A+B}{2})\cdot cos(\frac{A-B}{2})=-cos(\frac{360-A-B}{2})\cdot cos(\frac{C-D}{2})$

$\iff cos(\frac{A+B}{2})\cdot cos(\frac{A-B}{2})=cos(\frac{A+B}{2})\cdot cos(\frac{C-D}{2})$

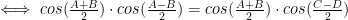
Lås oss anta att cos (A + B)/2 är skiljt från 0. Då får vi:

$cos(\frac{A-B}{2})=cos(\frac{C-D}{2})$

$\Rightarrow cos(A-B)=cos(C-D)$

$\Rightarrow A-B=\pm(C-D)$

Eftersom C och D är godtyckliga kan vi ignorera vårt +/- i högerledet, och vi får:

$A-B=C-D \iff A+D=B+C$

Vi får alltså att ifall cos (A + B)/2 är nollskiljt så kommer A,D och B,C vara par av supplementära vinklar.

Vi noterar att cos (A + B)/2 = 0 implicerar att (A + B)/2 = 90 eller 180, och alltså att A + B = 180 (ty A + B + C + D = 360, och alla vinklar är positiva, så A + B = 360 är ingen möjlighet).

Med andra ord, tar vi två godtyckliga vinklar i vår fyrhörning och kallar dem A och B, då gäller att A + B = 180 eller så är A + D = 180, där D är någon annan vinkel. Alltså är vi garanterade att vinklarna i vår fyrhörning är parvis supplementära.

Vi får två möjligheter, att intilliggande vinklarna är supplementära eller att motstående vinklar är det. Ifall de är intilliggande får vi att två sidor i vår figur är parallella, och vi har alltså en paralleltrapets. Och ifall motstående vinklar i en fyrhörning är supplementära, då är fyrhörningen cyklisk.

Sammanfattningsvis har vi alltså funnit att om summan av cosinus av alla vinklar är 0, då gäller att antingen så är varje vinkel supplementär till en intilliggande vinkel (och då är fyrhörningen en parallelltraptes) eller så är motstående vinklar supplementära (och där är fyrhörningen cyklisk), vilket skulle bevisas.

Adventspyssel 20

Möbelfabriken

Tre kandidater till jobbet på en möbelfabrik fick en uppgift på intervjun. De fick beskriva hur man avgör huruvida en bordskiva är formad som en kvadrat eller inte.

Den första kandidaten föreslog att man skulle jämföra bordskivans sidor med varandra, den andra tyckte att man skulle mäta diagonalerna och se ifall de var lika, den tredje tyckte däremot att man skulle jämföra de fyra strecken som bildas då diagonalerna skär varandra.

Vem av kandidaterna har störst chans att få jobbet?

Visa svaret

Adventspyssel 14

Finns det något bra ord för att någonting är någon yta, fast utvecklad och tillplattad? Det heter i alla fall ”net” på engelska.

Möjliga kuber

Vilka av figurerna på bilden kan vecklas ihop till en kub?

Visa svaret

Adventspyssel 9

Som vanligt med adventgåtorna får ni skriva om ni har frågor, en lösning eller vill tipsa mig om något liknande.

Tändstickor

Du har 6 tändstickor och med hjälp av dem ska du bygga en figur som består av 4 liksidiga trianglar. Hur ska du göra om tändstickorna inte får brytas itu och du måste använda alla tändstickor?

Visa svaret

Lösningen till problemet för de yngre vecka 45

Mattegåta

En chokladtårta är rektangelformad och sju personer ska dela på den. På tårtan finns 7 marsipanrosor:

Hur kan man dela tårtan i sju delar så att det finns en ros i varje del, om man bara får skära tårtan tre gånger och skärningarna måste vara raka linjer? Observera att delarna inte behöver vara lika stora.

Diskussion

Om det till en början inte verkar gå med tre linjer, tänk på vad tre linjer kan bilda för konfigurationer vid sidan av tårtan. Tre linjer som inte korsar varandra i en och samma punkt och som inte är parallella bildar en triangel och sex oändliga delar om de ritas på ett oändligt plan.

Sju är det maximala antalet delar, så linjerna på tårtan ska bilda någon liknande figur (det ska vara en ros i varje del).

Ett annat sätt att komma fram till svaret är att rita en linje i taget. Om man tänker från slutet, måste varje del på tårtan innehålla högst två rosor innan sista linjen ritas (så att den eventuellt skär på dessa delar). På samma sätt, måste varje del innehålla högst fyra rosor innan den andra linjen ritas. Så den första linjen som ritas måste dela tårtan i två delar: en med tre rosor och en med fyra.

Lösning (av Nicklas Yttergren)

Så här till exempel:

Matteproblem för de yngre vecka 45

Mattegåta

En chokladtårta är rektangelformad och sju personer ska dela på den. På tårtan finns 7 marsipanrosor:

Matteproblem för de yngre vecka 38

Mattegåta

Jon-Erik har en triangel utan några markeringar, som är gjord av plast. Triangeln är rätvinkling och har förutom vinkeln 90° också vinklarna på 60° och 30°. Hur kan Jon-Erik konstruera en vinkel på 15° om han inte får använda några andra redskap än plasttriangeln och papper?

Matteproblem för de äldre vecka 38

Mattegåta

En cirkel är ritad på koordinatplanet och dess mittpunkt har koordinaterna (a,b). Man vet också att origo hamnade inuti cirkeln.

Om S⁺ är den totala arean av delarna i cirkeln, som består av punkter med samma tecken på koordinaterna och S^– är totala arean av delarna med punkter som har olika tecken på koordinaterna, vad är S⁺-S^– lika med?

Lösningen till problemet för de yngre vecka 35

Mattegåta

Cissi fyllde år så hon bakade en tårta till sin födelsedag. Tårtan var dock inte rund, utan formad som en regelbunden sexhörning ABCDEF. Cissi markerade K och L, som var mittpunkterna på sidorna EF och FA respektive. Sedan skar hon längs med BK och sedan längs med LC. Hanna fick den triangulära biten BOC, medan Sofie fick den fyrkantiga biten KOLF. Vilken tjej fick mer tårta?

Diskussion

När två figurer har så olika form som Hannas och Sofies bitar, är det svårt att jämföra dem. En idé är att ge dem mer tårta, men exakt lika mycket var. Sedan jämför vi de större bitarna.

Lösning

Se hur mycket tjejerna får om de också fördelas var sin bit OKEDC:

Men om vi roterar ena hexagonen, så ser vi att det egentligen är lika mycket tårta! Därför fick Hanna och Sofie lika mycket tårta även i början.

Lösningen till problemet för de äldre vecka 35

Mattegåta

Hitta det största antalet kongruenta icke-konvexa polygoner som man kan dela in en kvadrat i, på så sätt att polygonernas sidor är parallella med kvadratens och inga två polygoner går att få ifrån varandra genom translation. Visa varför just det antalet fungerar och varför det inte går med ett större.

Diskussion

Hur ska den här konstiga formuleringen tolkas?

Jo, att polygonerna har bara lodräta och vågräta sidor, så vinklarna överallt är 90 grader (eller 270). Och att alla figurera är kongruenta.

Vad betyder det att två figurer är kongruenta? Med det menas att man kan ta första figuren, flytta den på något sätt och precis täcka den andra figuren. Man får rotera och vända på den första figuren som man vill.

Faktum är att alla sådana här rörelser antingen är rotationer, speglingar, translationer eller kombinationer av de tre sakerna. Vi vet att rena translationer är förbjudna enligt uppgiften. Så det gäller att bestämma antalet sätt att rotera och spegla en figur så det alltid blir olika positionerade figurer. Sedan ska man hitta på ett exempel med det antalet också.

Lösning (av Erik Thörnblad)

Jag hävdar att åtta är det maximala antalet:
Bevis:
Rimligtvis har polygonerna hörn. Kolla på ett specifikt hörn. Kalla ena änden för A och andra änden för B. När man sedan roterar polygonen och bara tittar på just det hörnet, så framgår det att det finns totalt åtta olika sätt att vrida hörnet på, så att sidorna hela tiden är parallella med kvadratens sidor (som jag nu antagit är lodräta och vågräta).

Detta innebär att man som mest kan skapa åtta polygoner som uppfyller alla krav som ställts.