Rekommenderad från: 17 år
[kkratings]
En konvex fyrhörning ABCD har kända sidlängder: AB = 5, BC = 10, CD = 14, DA = 11. Fyrhörningens diagonaler skär varandra med en viss vinkel. Hur stor är den vinkeln?
Aladdin och grottan
Rekommenderad från: 12 år
[kkratings]
Aladdin vill komma in i grottan, men dörren än stängd. Innanför grottan finns en tunna med fyra hål (hålen är likadana och är placerade som hörnen på en kvadrat). I varje hål finns en karaff med en fisk inuti. Varje fisk kan antingen ligga med huvudet eller stjärten upp. Aladdin kan stoppa in händerna i två av hålen, känna efter hur fiskarna ligger där och vända på ingen fisk eller en fisk eller båda om han vill. Efter det snurrar tunnan och när den stannat kan han inte avgöra vilka hål han stoppade händerna i förra gången. Dörren till grottan öppnas när alla 4 fiskar ligger likadant. Aladdin har 5 försök på sig. Kommer han att kunna komma in?

Ett osannolikt möte
Tack till Lisa Lokteva för att hon tipsade mig om nedanstående problem:
Rekommenderad från: 15 år
[kkratings]
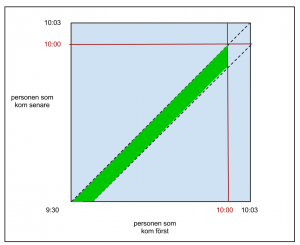
Två personer anländer oberoende av varandra till en bestämd plats mellan 9.30 och 10.00. De stannar på platsen i exakt tre minuter. Hur stor är sannolikheten att de möts?
Källa: Fibonaccitävlingen
Polisbilen
Rekommenderad från: 15 år
[kkratings]
En polisstation befinner sig på en väg som sträcker sig oändligt långt åt båda håll. Någon stal den gamla polisbilen, som har maxhastigheten lika med 90% av den nya polisbilens maxhastighet.
Detta upptäcktes på polisstationen och en polis fick i uppdrag att jaga ifatt tjuven med hjälp av den nya polisbilen. Polisen vet dock inte vare sig när tjuven stal den gamla bilen eller åt vilket håll tjuven åkte. Kan polisen komma ifatt tjuven?

Problemkonstruktör: G.Galperin
Fiskens bana
Rekommenderad från: 12 år
[kkratings]
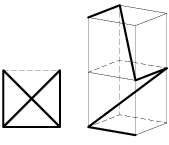
Någon antecknade fiskens bana i ett akvarium sett framifrån (första bilden) och någon annan ritade banan sett högerifrån (andra bilden). Hur såg fiskens bana ut om man kollade uppifrån?
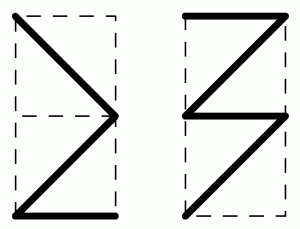
Problemkonstruktör: A.Shen
Pilen
Rekommenderad från: 10 år
[kkratings]
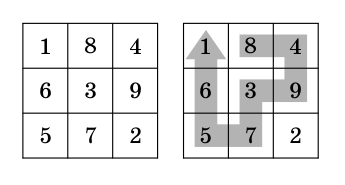
Siffrorna 1 till 9 fyller kvadraten som det syns på den vänstra bilden. Man får gå på kvadratens rutor, men aldrig tillbaka till en ruta man varit på förut, och man måste alltid gå till en angränsande ruta.
Katarina gick längs med pilen som syns på den högra bilden. Hon skrev ner siffrorna som hon gick på i ordning och fick talet 84937561. Rita en annan väg, som ger ett större tal (ju större tal, desto bättre).
Lejonet på arenan
Grattis på pidagen!
Rekommenderad från: 17 år
Förkunskaper: radianer, transformationer.
[kkratings]
Ett lejon springer runt på en rund cirkusarena, som har radien 10 m. Lejonets bana består av raka streck och i slutändan springer han 30 km. Visa att summan av alla vinklar, som lejonet svängde under springturen, är minst 2998 radianer.

Källa: Kvant magazine
Annorlunda tideräkning
Rekommenderad från: 12 år
[kkratings]
Invånarna på Matteön delar in dygnet i timmar, timmar i några minuter och minuter i några sekunder. Men deras dygn består av 77 minuter och deras timme innehåller 91 sekunder. Hur många sekunder ingår i ett dygn på Matteön?
Källa: Математический праздник
Spänd tråd
[kkratings]
I en vägg sitter tjugo spikar (se bilden). Avståndet mellan två spikar som sitter precis bredvid varandra är 1 cm.

Din uppgift är att spänna en 19 cm lång tråd mellan spik 1 och spik 2, så att den går igenom alla spikarna. Hur gör du?
Språkkunskaper
[kkratings]
På en gymnasieskola tillfrågade man alla elever om vilka språk de kunde. Det visade sig att fler än 90% kunde både engelska och tyska, samt att fler än 90% kunde både engelska och franska.
Visa att bland de elever som kan franska och tyska, kan fler än 90% också engelska.

Källa: Tournament of Towns
© 2009-2024 Mattebloggen