Rekommenderad från: 11 år
[kkratings]
Min bror ställer in datumet varje dag med hjälp av fem träblock.

Tre av dem är av avlånga och används för månaderna.

De andra två är kuber. Vilka siffror kan stå på kubernas sidor för att man ska kunna bilda alla datum?
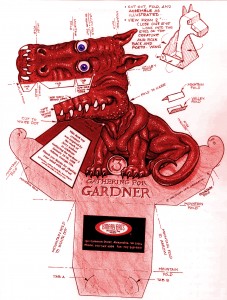
Gardners drake
Du har säkert bilder eller monument där någon tycks följa dig med ögonen när du passerar. Men har du någonsin träffat en konstgjord varelse som följer dig med hela huvudet?
(Vänta ett tag innan videon laddas, det är värt besväret!)

Synvillan fungerar bra på film
När kameran filmar, så registerar ”bara” den 2-dimensionella bilden, precis vad som skulle hända om du skulle kolla på världen med bara ett öga. Med ett öga ser du en platt bild, men med hjälp av ljussättningen, storlekar och din kunskap om världen uppfattar du ändå hur långt bort saker är. Det andra ögat ser en egen platt bild, men ser världen ur en annan vinkel. Eftersom hjärnan är medveten om de här vinklarna kan den lägga på de platta bilderna på varandra och du får ännu bättre djupseende. (Testa att titta ut genom fönstret, blundandes med ett öga. Öppna sedan det andra ögat och sedan blunda med det igen, öppna igen, blunda igen och så vidare. På så sätt kan du avgöra hur djupt du egentligen ser med bara ett öga.)
Hjärnan ser ett djup i taget
Problemet uppstår när två olika tredimensionella objekt har samma projektion, det vill säga den platta bilden som en kamera skulle registrera. Hjärnan kan då inte se två tredimensionella objekt samtidigt, utan måste växla och tycka en sak i taget.
Precis som att du inte kan se en anka och en kanin samtidigt på den här bilden:

så måste du bestämma dig i varje stund om den lilla kuben är en utbuktning eller ett hål:

Varför draken ser dig
Eftersom vid är vana vid tredimensionella objekt som ”buktar ut” snarare än ”buktar in”, så väljer hjärnan att tolka drakhuvudet som fylligt om vi kollar på draken med bara ett öga (ibland fungerar det även om vi kollar med två). Istället för att se drakhuvudet för det inbuktade fusket det faktiskt är, så går hjärnan hellre med på att draken följer oss med huvudet hur vi än tittar på den. Drakens konstruktion är baserad på design av Jerry Andrus.
Tillverka själv
Rekommenderas för: alla åldrar, men för att draken ska fungera krävs noggrannhet, så någon över 12 år borde närvara
Materiel: utskrifter med drakar, sax, lite tejp eller lim
Tid: 30 minuter för tillverkning, samt 30 minuter för tokigt tittande på den färdiga draken.
Ladda ner en drakbild och skriv ut på en A4. Instruktionerna finns på bilden, men är på engelska. Det du behöver veta är att ”mountain fould” betyder att man ska vika pappret som ett ”berg” längs med linjen, det vill säga så att spetsen utgörs av sidan med drakbilden, och att ”valley fould” är tvärtom.
Börja med att klippa ut hela draken och lägg den sedan tillbaka till resten av pappret för att se de exakta instruktionerna. Har du några frågor om konstruktionen, skriv i kommentarerna!
Korstal 2012
Korstal 2012
[kkratings]
Fyll i precis som ett vanligt korsord (fast nu endast med siffror). Obs! Inga tal börjar med noll.

Vågrätt:
1. Tvåpotens.
6. Siffersumman för lodrätt 13, skrivet baklänges.
7. Närmsta årtalet i framtiden som skrivs med bara två olika siffror.
9. Årtal i det förflutna som var precis emellan två skottår.
10. Siffersumman för vågrätt 15.
11. Delbart med 4 olika primtal.
12. Om jag delar min ålder med 2 och sedan adderar 5, så får jag hur gammal jag var för 8 år sedan. Vilket år är jag född?
15. En kub.
18. Produkten av lodrätt 14 och lodrätt 16.
19. En summa av två olika kvadrattal.
Lodrätt:
1. Delbart med 9.
2. Siffrorna i talet bildar aritmetisk talföljd.
3. Delbart med 10101.
4. Produkten av siffersumman för vågrätt 10 och den positiva sifferdifferensen för vågrätt 10.
5. Talet ser likadant ut vänt upp-och-ner.
8. Siffrorna i talet kommer i avtagande ordning.
13. Ett primtal.
14. Hur gammal blir jag nästa år?
16. Har udda antal delare.
17. Har samma siffersumma som lodrätt 13.
Att dela rättvist
Att dela rättvist
[kkratings]
En vandrare gick förbi två kompisar som skulle äta pannkakor. Ena kompisen hade 3 pannkakor, den andra hade 4 pannkakor. Alla pannkakorna delades jämnt mellan de tre personerna. Vandraren betalade sedan för sig med 7 kronor. Hur ska kompisarna dela pengarna rättvist mellan sig (det vill säga att pengarna var och en får motsvarar mängden pannkakor var och en gav bort)?
Datum med två siffror
Datum med två siffror
[kkratings]
Dagens datum är lite ovanligt: 121222. Vilket blir nästa datum som skrivs med högst två olika siffror (om datumet betecknas med 6 styken siffror)?
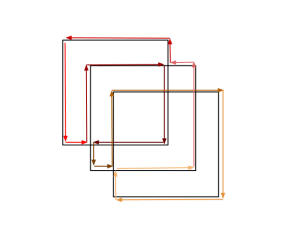
Att rita tre kvadrater
Att rita tre kvadrater
[kkratings]
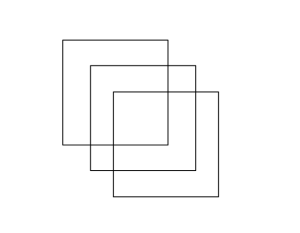
Går att rita följande figur utan att lyfta pennan från pappret? Det är inte tillåtet att dra samma sträcka flera gånger.
Val i Bananrepubliken
Val i Bananrepubliken
[kkratings]
I riksdagsvalet i Bananrepubliken deltog alla landets medborgare. Alla som röstade på Clementinpartiet tycker om clementiner. Bland dem som röstade på de andra partierna tycker 90% inte om clementiner.
Hur stor procent röster fick Clementinpartiet i valet om 46% av Bananrepublikens invånare tycker om clementiner?

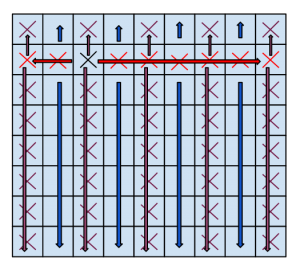
Kryssa grannrutor
Kryssa grannrutor
[kkratings]
Chiyen satte ett kryss i en ruta på en rektangel. Esteban får sätta kryss i de andra rutorna, men bara om de uppfyller följande regel: man får bara kryssa i rutor som har ett udda antal grannrutor med kryss (med grannrutor menas de som delar en sida med rutan).
Kan Esteban kryssa i alla rutorna på rektangeln, oavsett vilken ruta som blev ikryssat av Chiyen, om rektangeln har storleken:
(a) 8×9 rutor?
(b) 8×10 rutor?

Bilar i Mexico
Bilar i Mexico
[kkratings]
Mexico bestämde sig för att införa en ny lag, som innebär att varje bil i landet måste stå obrukad minst en dag i veckan (ägaren måste meddela polisen vad registreringsnumret är och vilken veckodag bilen inte kommer vara i bruk).
I en viss mexikansk familj vill vuxna åka bil varje dag (var och en behöver en bil för att utföra egna ärenden). Hur många bilar måste de som minst ha, om det finns
(a) 5 vuxna
(b) 8 vuxna
i den familjen?
Rubiks kub utan hörn
Rubiks kub utan hörn
[kkratings]
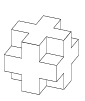
Man tog bort alla hörn från en Rubiks kub. Skulle en sådan konstruktion kunna sättas ihop av rätblock med 1×3-kuber?
© 2009-2025 Mattebloggen