Mattebloggen

Måla egna fraktaler

Har du alltid velat att rita egna fraktaler, men inte vetat hur man gör?

Grundprincipen för en fraktal är ett mönster som upprepar sig inuti figuren om och om igen. De mest kända exempel är:

Sierpinskis triangel

En liksidig triangel delas upp i fyra likadana delar och den mittersta lämnas oberörd. Samma sak händer med de andra tre delarna: var och en av dem delas upp i fyra och den mittersta lämnas oberörd. Fortsätt i alla oändlighet och du får Sierpinskis triangel!

Random_Sierpinski_Triangle_animation — Lite alternativ framställning av samma fraktal

Kochs snöflinga

Börja återigen med en liksidig triangel. Sudda bort de mittersta tredjedelarna på varje sida och rita två sidor som om det fanns en till liten liksidig triangel där. Fortsätt med de små nya sidor som bildats och så vidare. Du får Kochs snöflinga!

Mandelbrotmängden

Mängdens beskrivning är lite mer avancerad, men denna fraktal är otroligt vacker. Mängden består av alla komplexa tal (varje tal motsvarar en punkt i mänden) sådana att en viss process inte sticker ut mot ändligheten när man sätter in detta tal som parameter.

Mandelbrot_sequence_new — Klicka på bilden!

Så hur kan man skapa egna fraktaler? Du kan komma på en process som du gör om med en figur om och om igen, i mindre och mindre skala. Sådana processer kalla för rekursiva, vilket innebär att varje bild beror på de föregående på ett fixt sätt.

Ett enklare sätt är att måla fraktalerna på Recursive Drawing, där det finns en möjlighet att lägga in en bild i sig själv. Titta på introduktionsvideon eller börja måla direkt. Det går att skapa snygga fraktaler på 5 sekunder!

Denna fraktal är gjord av en enkel form (pinne med löv) lagd på sig själv:

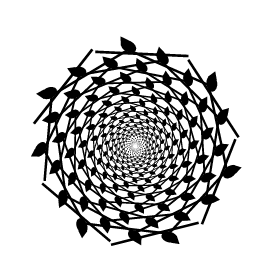
Sierpinskis ”triangel” tog däremot långt tid att skapa:

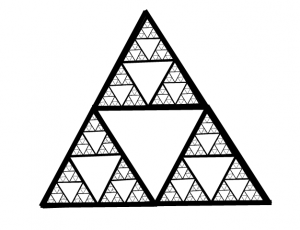
Försök att göra det själv!
Kan du komma på ett sätt att rita en triangelform i programmet? Hur gör man sedan så att bilden kopieras i sig själv tre gånger och inte en?

Roliga spel med tråkiga ekvationer

De flesta människor tycker inte om algebra i skolan. Utan någon intuition för vad som händer tvingas de att lösa ekvationer i skolan. Och när ekvationen väl är löst finns det ingen känsla av tillfredsställning, snarare kvarstår förvirringen och tankarna som ”vad har jag precis gjort och varför var det bra?” dyker upp.

Många gånger har jag hört begreppet ”gamifiering” (”gamification” på engelska) nämnas i sådana diskussioner. Att göra om aktivitet i skolan till ett spel skulle göra det intressant för eleven att slutföra det. Små belöningar, även bara orden ”level completed”, kan motivera en att gå vidare. Dessutom erbjuder spel mer variation än mekanisk räkning.

Jag tror också på att spel är framtiden inom matematikundervisning. Än så länge har jag hittat två bra spel som handlar om ekvationer. Båda förverkligar en idé, till skillnad från massa andra spel som endast överför tråkig räkning från skrivblocket till datorn.

Den första är skapad av fieldsmedaljören Terence Tao. Hans tanke med spelet är att lära ut balansmetoden (det vill säga att man förändrar båda ekvationsled på samma sätt samtidigt), men samtidigt göra det intressant. Med begränsade operationer ska man lösa ut x så fort som möjligt. Även personer som är bra på matte kan få utmaning av de sista nivåerna.

Spela Terence Taos spel (tryck på bilderna på gubbarna, inte deras instruktioner).

Det andra spelet handlar om linjer och deras ekvationer. Enkel idé, briljant utförande!

Spela Algebra vs. Cockroaches

Bäst resultat vinner!

Den senaste träffen på Katedralskolan genomförde vi en liten tävling bland deltagarna.

Varje deltagare fick 5 stycken problem att lösa på kort tid. Dock behövde inte problemen lösas fullständigt, utan det viktiga var att uppnå ett resultat. Men jämna mellanrum samlade jag in resultaten på varje problem. Sedan får det sämsta resultatet 1 poäng, nästa resultat får 3 poäng och så vidare.

Till exempel, när det hade gått 5 minuter av tävlingstiden så lämnade deltagarna in sina svar (tillsammans med exempel) på problem 1. Säg att deltagarna lyckas med svaren 20, 22, 20 och en lösning är felaktig. I det här fallet är det bra att ha så litet svar som möjligt. Personen med svaret 22 får då 1 poäng, personerna med svaren 20 får då 4 poäng var (de delar jämnt på 3- och 5-poängaren). Personen utan giltig lösning får inga poäng.

Testa själv att uppnå så bra resultat som möjligt på 25 minuter. Läs igenom problemen först och starta sedan klockan. Posta gärna dina bästa resultat i kommentarerna sedan, så kan vi se vem som vinner ”tävlingen” här på bloggen.

Fem minuter per problem

1. Placera springare på schackbrädet 8×8 för att de ska angripa samtliga lediga rutor. Ju få springare desto bättre.

2. Skriv ner på en rad några på varandra följande positiva heltal som har siffersummor ej jämnt delbara med 8. Ett exempel: 18, 19, 20. Ju fler tal desto bättre.

3. Fyll i en tabell av format 3×5 med olika positiva heltal. Summan i ett vilket som helst par grannrutor skall inte vara jämnt delbart med 3. Som grannar räknas rutor med en gemensam sida eller ett gemensamt hörn. Ju mindre det största talet i tabellen blir desto bättre.

4. Hitta ett tal med samma siffersumma som siffersumman hos 1992 och samma sifferprodukt som sifferprodukten hos 1992. Ju större talet är desto bättre.

5. Det finns tillräckligt många kort med talen 9, 49, 169, 289, 729 och 625. Plocka ut ett antal kort med summan 2004. Ju färre kort desto bättre.

Problemlösning lådprincipen

Den här vårterminen har jag äran att tillsammans med en annan lärare leda problemlösningskursen på Katedralskolan i Uppsala! Vi håller 2 timmarslektioner för intresserade elever på skolan, samt för nior som ska börja läsa där.

Tanken med träffarna är att träna eleverna inför kommande tävlingen SMT (SM i matte för gymnasister) och utveckla elevernas problemlösningsförmåga. Framförallt ska vi ha kul och upptäcka spännande ny matte tillsammans.

Problemlösning intro
Problemlösning heltalsekvationer

Nedan är den tredje lektionen som jag höll i (femte lektionen totalt).

Problemlösning Katedralskolan, 2012-05-09

Lådprincipen

“Om tio duvor sitter i nio lådor, så måste någon låda innehålla minst två duvor”

0. På en skola går 400 elever. Visa att två av dem fyller år samma dag.

1. a) Niklas har en stor låda med vita och svarta strumpor. En morgon har han bråttom och vill få ett par matchande strumpor så snabbt som möjligt ur lådan. Hur många strumpor måste han dra upp på måfå för att vara säker på att få ett par av samma färg?

b) Samma fråga, men med tre färger.

c) Det finns nu 10 vita, 10 röda samt 10 vita strumpor i lådan. Hur många strumpor ska Niklas dra på måfå för att vara säker att få upp alla olika färger?

2. I en granskog växer en miljon granar. Varje gran har som mest 200000 barr. Visa att det finns två träd i skogen med samma antal barr.

3. Det finns 15 pyttesmå hål i en maläten matta 4m×4m. Visa att man kan klippa ut en liten matta av storlek 1m×1m som är utan hål.

4. a) Givet 10 positiva heltal, kan det hända att alla möjliga skillnaderna emellan dem är ej delbara med 10?
b) Givet 11 positiva heltal, kan det hända att alla möjliga skillnaderna emellan dem är ej delbara med 10?

5. På Jorden utgör havet mer än hälfen av planetens yta. Visa att det finns två diametralt motsatta punkter på planeten, som båda ligger i havet.

6. 65 elever gjorde nationella provet i Engelska B. På mutliga, skriftliga respektive förståelsedelen kunde man få IG, G, VG eller MVG. Stämmer det att man kan hitta två elever som fick samma betygskombination?

7. Visa att vilka fem personer man än tar, så har två av dem samma antal kompisar i den gruppen.

8. Visa att vilka 52 heltal man än tar, så går det att hitta två vars summa eller skillnad är delbar med 100.

9. På ett militärlager finns kängor i storlek 41, 42, 43, två hundra kängor av varje storlek. Totalt är det tre hundra vänsterkängor och tre hundra högerkängor. Visa att man kan bilda åtminstone 100 par kängor som matchar.

Extraproblem. Visa att bland 6 personer går det alltid att hitta tre som känner varandra eller tre som inte känner varandra.

Polisbilen

Rekommenderad från: 15 år

[kkratings]

En polisstation befinner sig på en väg som sträcker sig oändligt långt åt båda håll. Någon stal den gamla polisbilen, som har maxhastigheten lika med 90% av den nya polisbilens maxhastighet.

Detta upptäcktes på polisstationen och en polis fick i uppdrag att jaga ifatt tjuven med hjälp av den nya polisbilen. Polisen vet dock inte vare sig när tjuven stal den gamla bilen eller åt vilket håll tjuven åkte. Kan polisen komma ifatt tjuven?

Problemkonstruktör: G.Galperin

Visa lösningen

En lektion för små barn i topologi

Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.

Här kan du se vad vi tidigare har gått igenom.

Former

Topologi handlar om olika slags former hos objekt. Båda barn och vuxna har bra intuition för former och hur de kan förändras, men ibland kan ointuitiva saker också hända:

Denna lektion skall vi experimentera med form hos olika sorts objekt med olika material.

Lera

När man ska förklara ordet topologi för någon som inte vet vad det är, så illustrera man ofta med detta exempel.

Man säger att en munk och en kopp är topologiskt sett samma, eftersom man kan omforma dem till varandra på ett naturligt sätt, om de nu skulle vara gjorda av modellera.

Lera är precis vad vi kommer pyssla med. Alla barn får var sin bit lera (t.ex. får alla var sin färg) och får i uppgift att tillverka en kopp med öra. Kan de göra det utan att riva leran någonstans? (Ńej, det kan de inte, så de får riva den här gången.) Kan de nu göra om koppen till en ring/en munk utan att riva leran? Det är tillåtet att klistra ihop leran, annars blir detta en väldigt opraktisk uppgift. I topologin får man egentligen inte klistra två punkter hur som helst om objektet ska behålla den topologiska formen.

Metalltråd

Även platta objekt kan vara topologiskt ekvivalenta eller inte. Till exempel kan siffrorna 1, 7 och 5 omformas till varandra, medan 9 och 6 tillhör en annan grupp. Skillnaderna är lättast att se om man tillverkar siffrorna i böjbart material, t.ex. snöre eller ståltråd och tydlig markerar platsen där materialet träffar sig självt igen (som i mitten på siffran 8).

Barnen får som första uppgift att på en bit ståltråd göra så många siffror den kan i rad. Början kommer att se ut ungefär så här:

Det viktiga är att tråden ska gå att räta ut igen!

Efter att barnen upptäcker att bara siffror 1,2,3,5 och 7 går att göra på det här sättet diskuterar vi hur det ligger till med andra siffror och sedan också bokstäver. Vilka stora bokstäver är till exempel i samma grupp som A?
(Svar: R)

Detta påminner om en gåta som folk länkar till då och då. Jag tror att det kan stämma att för mycket matematikutbildning skadar om man ska lösa gåtan fort:

8809 = 6
7111 = 0
2172 = 0
6666 = 4
1111 = 0
3213 = 0
7662 = 2
9312 = 1
0000 = 4
2222 = 0
3333 = 0
5555 = 0
8193 = 3
8096 = 5
7777 = 0
9999 = 4
7756 = 1
6855 = 3
9881 = 5
5531 = 0

2581 = ?

Knutar

Barnen får två snören var för att experimentera med knutar. Först får de försöka knyta enligt schema, som denna knut:

Sedan gäller det att först gissa utifall bilden ger oss en knut eller inte utan att försöka göra knuten själv. Har man en gissning får man prova att bevisa det med hjälp av sitt snöre.

Flätor

Knutar är ganska enkelt för större barn, så de får gå vidare till flätor. Det finns förstås den vanliga flätan, som man gör med tredelat hår. Men det är inte bara den vi ska experimentera med.

Även fyra delar kan ge en fläta:

Och fem förstås:

Uppgifter utan ord

Jag är alltid mycket för den visuella matematiken. En bild säger verkligen mer än tusen ord. Uppgiften nedan som vi avslutar med (den har inte så mycket med topologi att göra) kommer ursprungligen från inläggetMath without Words.

Problemlösning heltalsekvationer

Nedan är den andra lektionen som jag höll i. Vi övade på att lösa ekvationer, där variablerna var heltal. Vi gick igenom uppgift 0 på tavlan och totalt sett löstet uppgifterna 1-5. Det var en svår lektion med andra ord.

Inte det roligaste ämnet heller inom problemlösning tycker jag, men sådana här uppgifter träffar man jämt på i SMT-kvalen.

Problemlösning Katedralskolan, 2012-04-25

Tal och ekvationer

0. Hur många lösningar har ekvationen xy = 10
a) i positiva heltal;
b) i heltal;
c) i reella tal?

1. Produkten av tre positiva heltal är 77 medan deras summa är mindre än 77. Bestäm summan.

2. Samtliga portar i ett hyreshus har samma antal våningar. Det finns lika många lägenheter på varje våning. Man vet att antalet våningar är större än antalet lägenheter per våning vilket i sin tur är större än antalet portar. Det finns minst två portar. Totalt finns det 105 lägenheter. Bestäm antalet våningar.

3. Bestäm samtliga positiva heltalslösningar till ekvationen 4x+7xy = 100.

4. Produkten av två positiva heltal är 19 större än kvadraten på det första talet. Bestäm det andra talet.

5. En 40-foting har ett huvud, en drake har tre huvuden. Det flyger en svärm av sådana djur. Det finns totalt
а) 26 huvuden och 298 fötter;
b) 39 huvuden och 648 fötter.
Hur många fötter har en drake?

6. Finns det sådana positiva heltal x och y att
a) x²-y² = 21;
b) x²-y² = 20;
c) x²-y² = 22?

7. Av en rutad kvadrat klipper man en mindre rutad kvadrat. Det finns 23 rutor kvar. Bestäm storleken på den större kvadraten.

8. Det är ett känt faktum att 1993 är ett primtal. Bestäm om det finns sådana positiva heltal x och y att
a) x²-y²=1993;
b) x³-y³=1993;
c) x⁴-y⁴=1993.

9. (SMT) Visa att talet 2009 kan skrivas som summan av 17 positiva heltal som endast innehåller siffran 7 och ange alla sådana framställningar. Två framställningar som skiljer sig enbart beträffande termernas ordning räknas bara en gång.

10. (SMT) Bestäm x² + y² + z² om x, y, z är heltal som uppfyller
x + y + z = 60
(x − 4y)² + (y − 2z)² = 2

Blandade problem

1. a) Man har suddat första siffran i ett tresiffrigt tal och multiplicerat det erhållna talet med 7. Då fick man det ursprungliga talet. Bestäm talet.
b) Man har suddat andra siffran i ett tresiffrigt tal och multiplicerat det erhållna talet med 6. Då fick man det ursprungliga talet. Bestäm talet.

2. (SMT) Differensen mellan tva femsiffriga heltal ar 246. Visa att de tio siffror som ingår i de båda talen inte alla kan vara olika.

Fiskens bana

Rekommenderad från: 12 år

[kkratings]

Någon antecknade fiskens bana i ett akvarium sett framifrån (första bilden) och någon annan ritade banan sett högerifrån (andra bilden). Hur såg fiskens bana ut om man kollade uppifrån?

Problemkonstruktör: A.Shen

Visa lösningen

Problemlösning intro

Nedan är första lektionen, som kan användas som introduktion till problemlösning för intresserade elever. Problemen 0 och 5 går man igenom på tavlan genom att tillsammans med eleverna få fram lösningen.

Problemlösning Katedralskolan, 2012-04-11

Startuppgifter

0. I en skål växer en bakteriekultur. Varje sekund delar sig alla bakterier i två nya. Efter en minut är skålen helt full med bakterier. Efter hur länge var skålen full till hälften?
(Ledtråd: tänk från slutet.)

1. En bit föll ur en gammal tidskrift. Första sidan hade numret 328 och sista hade ett nummer som bestod av samma siffror, men i en annan ordning. Hur många sidor föll ut ur tidskriften?

2. Du har tillgång till 24 kg spikar och en balansvåg med två skålar. Hur kan du mäta upp 9 kg spikar?

3. En snigel tar sig upp för en påle, den börjar från markens nivå. Varje dag kommer snigeln upp 5 cm, medan varje natt åker den ner 4 cm. När kommer snigeln upp till toppen, om pålen är 75 cm lång?

4. Ta bort 10 siffror från talet 1234512345123451234512345, så att talet som står kvar är så stort som möjligt.

Problemlösningstips 1: lös ett “förenklat” problem

5. I en 5×5-tabell står det ett plustecken i en hörnruta och i alla andra rutor står ett minustecken. En tillåten operation är att invertera alla tecken i en hel rad eller en hel kolonn. Går det att genom tillåtna operationer få alla tecken till att vara plus?
(Svar: nej. Ledtråd: titta på samma problem för en 2×2-tabell)

6. Det finns en träkub med sidan 3 cm. Det är ganska lätt att såga upp den i 27 små kuber med sidan 1 cm genom att såga sex gånger. Går samma sak att genomföra med färre sågningar om det är tillåtet att flytta bitarna emellanåt?

7. Visa att en konvex polygon med n hörn har vinkelsumman 180(n-2) grader.

8. Visa att n(n+1)(n+2) är delbart med 6 för alla heltal n.

9. Lös ekvationen (x²+x-3)²+2x²+2x-5 = 0

Logikövningar

10. I ett hav bor många olika bläckfiskar. Om en bläckfisk har jämnt antal armar så talar den alltid sanning, men om den har udda anta armar så ljuger den alltid. En gång sade den gröna bläckfisken till den mörkblåa:
– Jag har 8 armar. Och du har bara 6.
Då blev den mörkblåa sur:
– Det är jag som har 8 armar. Du har bara 7.
Den svarta bläckfisken höll med:
– Den mörkblåa har verkligen 8 armar. Men jag har hela 9!
Varpå den randiga bläckfisken sade:
– Det är ingen av er som har 8 armar! Bara jag har 8.
Vilka bläckfiskar hade exakt 8 armar?

11. I ett land finns endast tre städer: Sannholm, Löngeborg och Turmö. Sannholmsborna talar alltid sanning, Löngeborgarna ljuger alltid och de som bor i Turmö turas om strängt att tala sanningar och lönger.
En dag såg en jourhavande brandsoldat en rök och telefonen ringde. ”Vi har en brand! ” ”I vilken stad brinner det? ” ”I Turmö ”. Till vilken stad skall brandkåren?

En lektion för små barn i mönster och spatial förmåga

Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.

Här kan du se vad vi tidigare har gått igenom.

Mönster

Väldigt mycket i matematiken handlar om att se mönster. Jag skulle vilja påstå att det mesta inom grundskolans matematik går ut på att lära sig se ett slags mönster i uppgifter för att kunna tillämpa metoder.

Mönster som 3 + 7 = 10 hjälper en att lösa uppgifter som 14 + 3 + 7 = 24.

Och ifall man är bra på att extrapolera mönster, kan man komma på formler alldeles själv!

Upprepningar

Gjorde ni också girlanger utav gubbar till julgranen? Pojkarna nedan är ganska enkla att göra, men hur gör man för att klippa ut en girlang med varannan kille, varannan tjej?

Se mönstret och fortsätt

Ett bevis på att man ser mönstret i bilden är att man kan fortsätta det. Och tvärtom, om man försöker fortsätta mönstret ser man kanske när det blir fel och när det blir rätt.

Om man väver några remsor kan man se ett mönster i hur de synliga bitarna är färgade. Vilka färger finns underst respektive överst där bokstäver A och E står?

Föreställ dig mönstret

Ju mer matematik man läser, desto mer behöver man tänka abstrakt. Det innebär ofta att föreställa sig saker som inte finns framför en. Ibland föreställer matematiker sig saker som ingen har sett (som till exempel fyrdimensionella objekt)!

Förmågan att föreställa sig fysiska objekt och förhållandet dem emellan kallas för spatialförmåga. Den är väldigt viktig för pilot- och militäryrket, och så förstås matematikerna. För att träna den skall de lite äldre barnen lösa följande pussel:

Utan att kvadratbitar får klippas ut och arrangeras om, skall man bestämma vilken på som ska vara på vilken plats. Det betyder att bitarna måste arrangeras om i huvudet. Du kan prova själv genom att fylla i en en följande tabell med motsvarande tal.

Föreställ dig något som inte syns

En klassisk uppgift är att bestämma hur många kuber ingår i konstruktionerna, utan att alla kuberna syns.

Efter att alla barnen har skrivit ner förlaget, bygger vi upp sktrukturen och räknar hur många kuber det faktiskt behövdes.

Perspektiv

De äldre barnen får träna spatialförmågan på ett tredimensionellt sätt. De får se en bild på kubens alla sidor (i utvikt format), och sedan avgöra hur tre av kubens sidor ska se ut när man kollar på den från olika vinklar.

Tillverka en kub

Vi ska kombinera några av de ovastående övningarna och tillverka en kub själva. För det första skall barnen lista ut vilka av kvadraternas sidor skall tejpas ihop med vilka. Sedan får alla ett papper med ett mönster.

Uppgiften är nu att klippa upp mönstret i 6 likadana kvadrater. Varje kvadrat klistras sedan på en av sidorna på någons kub.

Det svåra är att klippa exakt utan att mäta. Tricket är att kolla på kanten, till exempel den vänstra. Då ska man klippa i bilden precis där den vänstra kanten av högra halvan är likadan som vänstra kanten av vänstra halvan. Skriv ut och försök själv!

minicubby.com