Mattebloggen

Matteproblem för de äldre vecka 36

Mattegåta

Ekvationen x²+px+q=0 har bara heltalsrötter och man vet att både p och q är primtal. Hitta p och q.

Lösningen till problemet för de äldre vecka 34

Mattegåta

Låt a^b beteckna talet a upphöjt till talet b. Man skall sätta ut parenteser i uttrycket 7^7^7^7^7^7^7 för att bestämma ordningen på operationerna (totalt kommer det att bli 5 parentespar).

Går det att sätta ut parenteserna på två olika sätt så att resultatet på uttrycket blir detsamma?

Diskussion

Jag tror inte någon formulering har diskuterats mer än just detta problemets här på bloggen. Det allra första som många visade för mig vad att problemet hade en enkel lösning, där svaret var ”ja”. Nämligen, att man ska sätta ut parenteser, som inte gör någonting, och på detta sätt uppnå samma resultat, som helt utan parenteser. Exempelvis: (7)^(7)^(7)^(7)^(7)^7^7 = (7^(7)^(7)^(7)^(7)^7^7), där båda är lika med 7^7^7^7^7^7^7.

Med detta svar blir dock problemet lite för ointressant för att finnas här på bloggen, så man kan börja misstänka att det är någon som har missat att säga något. Det är inte så uppenbart från problemets formulering, men det är faktiskt så att 7^7^7^7^7^7^7 (än så länge) är odefinierat. Visst, värdet är definierat för $7^{7^{7^{7^{7^{7^7}}}}}$ , det vill säga för potenser (fundera på vad operationsordningen är här), men inte för vår abstrakta symbol ”^”, som i problemets formulering definierades som en operation mellan två tal.

Med andra ord var det inte en slump att just 5 parentespar behövdes. Även tex tvingade mig att sätta ut måsvingarna för att skriva formeln ovan. Just 5 parentespar, där alla är väsentliga, kommer att bestämma ordningen för upphöjningarna. Nu när vi vet problemets exakta formulering, har vi en chans att lösa det. En sak värd att notera är att det inte spelar någon roll att vi håller på med just talet sju.

Lösning

Notera att (7^(7^7))^7=(7^7)^(7^7). Detta gäller på grund av regeln (a^b)^c = a^(bc) = (a^c)^b. Således kan resterande 3 parentesparen sättas ut på ett likadant sätt på båda uttrycken och deras värde förblir detsamma:
Exempel: ((((7^(7^7))^7)^7)^7)^7=((((7^7)^(7^7))^7)^7)^7

Matteproblem för de yngre vecka 35

Mattegåta

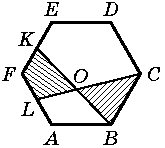
Cissi fyllde år så hon bakade en tårta till sin födelsedag. Tårtan var dock inte rund, utan formad som en regelbunden sexhörning ABCDEF. Cissi markerade K och L, som var mittpunkterna på sidorna EF och FA respektive. Sedan skar hon längs med BK och sedan längs med LC. Hanna fick den triangulära biten BOC, medan Sofie fick den fyrkantiga biten KOLF. Vilken tjej fick mer tårta?

Matteproblem för de äldre vecka 35

Mattegåta

Hitta det största antalet kongruenta icke-konvexa polygoner som man kan dela in en kvadrat i, på så sätt att polygonernas sidor är parallella med kvadratens och inga två polygoner går att få ifrån varandra genom translation. Visa varför just det antalet fungerar och varför det inte går med ett större.

Matteproblem för de yngre vecka 34

Mattegåta

Hitta två äkta bråk, det ena med nämnaren 8 och det andra med nämnaren 13, så att differensen mellan det största och det minsta av dem är så liten som möjligt.

Matteproblem för de äldre vecka 34

Mattegåta

Låt a^b beteckna talet a upphöjt till talet b. Man skall sätta ut parenteser i uttrycket 7^7^7^7^7^7^7 för att bestämma ordningen på operationerna (totalt kommer det att bli 5 parentespar).

Går det att sätta ut parenteserna på två olika sätt så att resultatet på uttrycket blir detsamma?

Lektioner från kollot

Snart är sommaren slut för min del och det är dags att sammanfatta vad jag lärt mig under mattekollotiden (jag var lärare för några av Rysslands mest skärpta åttor):
1. Åttan är lite för tidig årskurs för att introducera begreppet grupp.
2. Komplexa tal definieras bäst som mängden av par av tal plus regler.
3. Ha med några stycken 15-spel när du undervisar om permutationer!
4. 2x2x2 – Rubiks kuber som smycken är snyggt.
5. Om man är oförsiktig i sina matteresonemang kan man missa att man egentligen behöver använda satsen om att maximum på kompakt mängd existerar.

Förutom det har jag lärt mig att föra krig mot getingar, gå upp 5 minuter innan lektionerna börjar och hitta dold matematisk betydelse i ryska poplåtar.

Sommaruppehåll 2010

Som vanligt åker jag till Ryssland där jag kommer att vara hela juli. Mitt uppdrag är att lära ryska barn matematik på ett mattekollo.

Bloggen är tillbaka i början av augusti, håll utkik efter den nya tävlingen i att lösa mattegåtor! Jag har funderat på att göra två olika tävlingar, en för grundskolan och en för de andra deltagarna, så kommer det nog att bli i höst.

Vi hörs! Ha en kanonsommar!

Lösning till problem vecka 23

En tärning låg på bordet. Den flyttades ett steg i taget genom att rullas över på en ny sida (som gränsade till sidan som nyss var i kontakt med bordet). Till slut hamnade tärningen på samma plats som i början med samma sida uppåt. Kunde den översta sidan vrida sig 90 grader i förhållande till startläget?

Svar:

Nej, det kunde den inte.

Lösning:

Låt oss beteckna kubens hörn med $A, B, C, D, A_1, B_1, C_1, D_1$ (sidan $A_1B_1C_1D_1$ ligger precis under sidan $ABCD$ ). Föreställ er att finns en liten tetraeder $ACB_1D_1$ som är gjord av ett annat material. Vi kommer att följa den tetraederns position allt eftersom tärningen rör sig.

Om tärningen rullas över en gång, kommer tetraedern befinna sig i samma läge som $BDA_1C_1$ hade från början, fast parallellfärflyttad. Och vice versa, $BDA_1C_1$ avbildas på en parallellförflyttning av tetraedern $ACB_1D_1$ .

För att tärningen ska komma tillbaka tillsamma ruta, måste den rullas ett jämnt antal gånger (föreställ er ett schackbräde på bordet, då byter rutan färg efter varje steg). Det innebär att den annorlunda tetraedern kommer att avbildas på sig själv.

Men om den översta sidan vrids 90 grader, så avbildas sidan $AC$ på sidan $BD$ , men den sistnämnda ligger utanför tetraedern av annorlunda material. Motsägelse.

Lösning till problem vecka 22

Det finns två potatisar med godtycklig form och storlek. Visa att man kan lägga på var sin bit koppartråd på deras ytor så att det bildas två böjda ringar (inte nödvändigtvis platta), som har samma form och storlek.

Erik T. förser oss med lösningen nedan. De andra lösningarna var iofs precis likadana, kanske med något annorlunda formuleringar.

Jag ångrar dock lite att folk ibland kan lite för mycket topologi, eftersom jag fick följande kommentar från Johan B. när jag publicerade problemet:

”Jag tror du måste göra något antagande om potatisarna.
Låt ena potatisen vara en fylld torus, men istället för att tvärsnitten är cirklar så är de kochkurvor. En eventuell koppartråd som inte vill vara fraktal måste följa med torusen runt och bilda cirklar. Deras radie kan begränsas underifrån genom att göra innerdiametern på torusen stor. Låt den andra potatisen vara en epsilonsfär, det finns inga cirklar av stor radie på dess yta.”

Man ska anta att potatisar ser ut som potatisar :) Det vill säga är släta 3-dimensionella mångfalder, för de som inte äter potatis.

Lösning:

Placera potatisarna så att de överlappar varandra (om man tänker sig att de inte består av solitt material utan kan ”gå in i varandra”). De skär då varandra i någon slags kurva. Men denna kurvan ligger på båda potatisarnas yta. Alltså kan man lägga två kopparbitar med samma form och storlek (ge dem samma utseende som kurvan) på två valfria potatisars ytor.