Mattebloggen

Fast på gräsmattan

Rekommenderad från: 14 år

[kkratings]

Fredrik står i mitten av en rund gräsmatta, som har radien 100 meter. Varje steg Fredrik tar är 1 meter långt. Varje gång han ska ta ett nytt steg anger han riktningen som han ska gå i. Anna har då möjlighet att ändra Fredriks riktning mot den motsatta.

Kan Fredrik att komma på ett sätt att komma av gräsmattan oavsett vad Anna gör? Eller kan Anna alltid hindra honom?

Visa lösningen

Plan för staden med torg

Rekommenderad från: 12 år

[kkratings]

I en stad finns 6 torg. Ur varje torg utgår 3 raka vägar till exakt 3 andra torg. Inga två vägar korsar varandra. Bland de tre vägarna, som utgår från samma torg, ligger ena vägen inuti vinkeln, som de andra två bildar (en vinkel är mindre än 180 grader). Rita en möjlig plan för staden.

v42

Visa lösningen

Fyra färger räcker

Rekommenderad från: 14 år

[kkratings]

Det finns ett rutigt papper. På det finns rektanglar som har sin gräns gående längs med rutorna. Varje rektangel består av ett udda antal rutor och inga två rektanglar har gemensamma inre rutor. Visa att det går att måla rektanglarna i fyra färger på så sätt att två rektanglar med samma färg aldrig har gemensam gränspunkt.

Visa lösningen

Spiken i lådan

Rekommenderad från: 11 år

[kkratings]

Cissi klippte ut två likadana figurer ur en stor kartong. Sedan la hon dem på bottnen av en rektangulär låda så att de delvis täckte varandra. Det visade sig att hela bottnen blev täckt.

Sedan slog Kalle in en spik i mitten av lådans botten. Kunde det bli så att spiken gick igenom ena figuren, men inte den andra?

Visa lösningen

Tvåpotensens sista siffra

Rekommenderad från: 15 år

[kkratings]

Det finns ett naturligt tal m, sådant att talet 2^m har siffersumma 8. Kan sista siffran i talet 2^m vara lika med 6?

Visa lösningen

Svar:

Det kan den inte! Jag har fått in tre stycken olika lösningar, så det är bara att välja och vraka.

För att kunna förstå lösningarna är det bra att kunna:

moduloräkning

Om två tal har lika rester vid division med ett och samma tal n, så säger man att de talen är kongruenta modulo n.

Till exempel så är talen 3 och 11 kongruenta modulo 4 eftersom båda ger rest 3 när man dividerar med 4. Även talet -1 är kongruent med 3 modulo 4.
Man kan också skriva 3 $\equiv$ 11 (mod 4)

delbarthetsprincipen för 3

Ett heltal är delbart med 3 om och endast om dess siffersumma är delbar med 3. Man kan också vara fancy och säga att ett tal är delbart med 3 om och endast om talets siffersumma är kongruent med 0 modulo 3.

Till exempel så är talet 450072456 inte delbart med 3, eftersom siffersumman är 4+5+0+0+7+2+4+5+7=34 och det talet går inte att dela jämnt på 3.

delbarthetsprincipen för 9

Liknar faktiskt delbarthetsprincipen för 3. Ett heltal är delbart med 9 om och endast om dess siffersumma är delbar med 9.

Till exempel så är talet 1111000011111 delbart med 9, eftersom siffersumman är lika med 9.

Det är även så att ett godtyckligt tal och dess siffersumma alltid ger samma rest vid division med 9, det vill säga det är kongruenta modulo 9.

Lösning 1 (den officiella):

Vi konstaterar att de första tvåpotenserna är 2, 4, 8, 16 och 32, samt att inget av dessa uppfyller kriterierna. Dock måste alla kandidater vara jämnt delbara med dessa tal.

Om ett tal har siffersumman 8 och slutar på 6 finns två möjligheter:

a) Talet har formen 2*10^k + 6 för något k>=1 (dvs 26, 206, 2006, osv.)

26 (=2*13) är inte en tvåpotens, alltså måste k>=2, men alla andra tal på formen
2*10^k är delbara med 8, medan 6 inte är delbart med 8. Således blir talet som
helhet (2*10^k + 6) ej delbart med 8. Vi kan alltså helt utesluta denna möjlighet.

b) Talet har formen 1*10^k + 1*10ⁿ + 6 för något k>n>=1 (dvs på formen 100..0100…06)

6 är inte delbart med 4, så resten får inte heller vara det, om summan skall vara delbart med 4. Det enda n sådant att 10ⁿ inte är delbart med 4 är n=1 (k kan inte vara så litet). Alltså måste talet ha formen 1*10^k + 16.

Vi ser dock på samma sätt att 16 inte är delbart med 32, så det får inte 10^k heller vara. För alla k>=5 är 10^k jämnt delbart med 32, så dessa förkastas.

Man kan nu pröva de återstående lösningarna (10016, 1016, 116) var och en, men närmare bestämt är 16 $\equiv$ 16 i modulo 32, så 10^k måste vara lika med 32-16 $\equiv$ 16 (mod 32). Det enda k som uppfyller detta är k=4, vilket ger 10016 = 2⁵ * 313, som på intet vis är en tvåpotens. För säkerhets skull kan konstateras att 1016=2³*127 och 116=2²*29.

Lösning 2 (den med perioder):

Att siffersumman av 2^m 8, kräver att 2^m är kongruent med 8 modulo 9.

Att 2^m slutar på 6, kräver att 4|m. Detta ser man genom att helt enkelt
göra en tabell av potenser av 2, och ser att den har period 4, om man bara
betraktar sista siffran.
2, 4, 8 (1)6, (3)2,(6)4, (12)8, (25)6,…

Så, vi undrar egentligen om det finns heltal k, så att 2^4k $\equiv$ 8 (mod 9).
Ekvivalent med att
16^k $\equiv$ 8 (mod 9)<=>
7^k $\equiv$ 8 (mod 9) (*)

Nu,
7¹ $\equiv$ 7 (mod 9)
7² $\equiv$ 4 (mod 9)
7³ $\equiv$ 1 (mod 9)
och nu har vi nått 1, så denna sekvens kommer upprepa sig om och om igen.

Alltså kan högerledet aldrig bli 8, och (*) kan ej lösas. Att (*) ej kan lösas
implicerar att 2^m ej kan sluta på 6 och samtidigt ha siffersumma 8.

Lösning 3 (den snygga):

Antag att ett sådant tal finns. Notera att 2^k endast slutar på 6 om k är jämnt (t.o.m delbart med 4, men jämnt räcker).
Då har 2^k-1 siffersumma 7 och är inte delbart med 3. Men k=2n så
2²ⁿ-1=(2ⁿ-1)(2ⁿ+1).
Märk att talen 2ⁿ-1, 2ⁿ och 2ⁿ+1 är tre stycken på varandra följande, så något utav dessa måste vara delbar med 3. Men det kan inte vara 2ⁿ, eftersom det är en tvåpotens.
Någon av faktorerna i uttrycket är således delbar med 3 och vi får motsägelse.

Minnesregler för trigonometri – del 1

Det finns vissa saker som man bara måste lära sig utantill. Det kan tyckas att det är det enda som gäller i matten, men det kan räcka ganska långt att kunna bara några få formler.

Till exempel så kan vi prata om trigonometri. Jag tänkte dela med mig lite tips om hur man bäst kommer ihåg det essetiella och hur det går att härleda allt det viktiga därifrån.

För det första måste man lära sig vad sinus och cosinus är för någonting.

Båda två är funktioner som ger ut ett tal, när man stoppar in en vinkel. Men vad är det för tal? När vinkeln är känd (och mindre än 90 grader), så kan vi rita en rätvinklig triangel med den vinkeln. Låt oss säga att vår vinkel kallas för x. Det går förstås att rita flera olika stora rätvinkliga trianglar med x, men det kommer inte spela någon roll.

Vi mäter sidorna på vår uppritade triangel och konstateterar att kateterna är a och b långa och hypotenusans längd betecknar vi c. Då är sinus värde lika med den motstående kateten genom hypotenusan och cosinus är den närliggande kateten genom hypotenusan. Alla likformiga trianglar har samma förhållande mellan sidorna, därför spelar det ingen roll vilken storlek på triangeln vi väljer.

ratvinklig_sin_cos

ratvinklig_kossa Men hur ska man komma ihåg vilken funktion som är vilken om man nyss har lärt sig dem? Tänk på att cos (cosinus) låter lite som ”kossa” och kossan den är lat, därför vill den vara nära sin vinkel (orkar inte gå till motstående sidan). Och sin är då den andra funktionen.

Ett annat sätt att komma ihåg det är att sinus är snäll och cosinus är elak. Så sinus offrar sig och går till den motstående sidan. Fler tecken på sinus snällhet och cosinus elakhet kommer vi se i del 2.

Om du nu kan lite vanlig geometri är det inga problem att räkna ut sinus och cosinus för flera kända vinklar! Här väljer jag att mäta vinklarna i grader.

De saker som du behöver kunna är:

– Pythagoras sats

– vad vinkelsumman i en triangel är

– att likbenta trianglar har basvinklarna lika

– att trianglar med lika basvinklar är likbenta

Vi kan då räkna ut vad sinus för vinkeln 30° är, om man inte minns det. Rita såklart först en rätvinklig triangel med en vinkel lika med 30°. Och eftersom vinkelsumman för vilken triangel som helst är 180°, så är den sista vinkeln lika med 180°-90°-30° = 60°.

90-60-30x2

Rita sedan upp en likadan triangel, fast spegelvänd, och för ihop halvorna. Det som bildas är förstås en ny triangel, eftersom vinklarna på 90° passar ihop och bildar en linje. Men notera att den stora triangeln har alla vinklarna lika med 60°, därför är den liksidig. Alltså är c = 2a.

Nu är det lätt att räkna ut sinus av vinkeln 30°.

$sin 30^\circ = \frac{a}{c}=\frac{a}{2a}=\frac{1}{2}$

På så sätt är det rätt enkelt att lista ut vad cos 60° är för någonting. Det är nämligen samma som sinus 30°, eftersom om vi kollar på de två olika spetsiga vinklarna i en rätvinklig triangel, så blir enas motstående sida den andras närliggande och tvärtom. Hypotenusen är densamma.

Men hur tar vi reda på sin 60° (och samtidigt cos 30°)? För det måste vi bestämma förhållandet b/c. Men eftersom $a^2+b^2=c^2$ (Pythagoras sats), så kan vi i vårt fall skriva:

$(\frac{1}{2}c)^2+b^2=c^2$
så $b^2=c^2-\frac{1}{4}c^2=\frac{3}{4}c^2$

Eftersom alla längder är positiva har vi $b=\frac{\sqrt{3}}{2}c$ och då är

$sin 60^\circ = cos 30^\circ = \frac{b}{c} = \frac{\frac{\sqrt{3}}{2}c}{c} = \frac{\sqrt{3}}{2}.$

Och hur gör vi nu med vinklarna 0°, 45°, 90° grader? Det går faktiskt att rita upp motsvarande triangel och ”triangel”. Fundera på vad sinus och cosinus för de respektive viklarna blir. Faciten kommer i nästa del.

Om man minns de här trianglarna är det möjligt att alltid räkna ut sinus eller cosinus som man behöver. Men om det är lite svårt med geometrin, finns det en rätt bra minnestabell.

Skriv upp alla ”kända” vinklar: 0°, 30°, 45°, 60° och 90°. Deras sinus och cosinus följer då ett intressant mönster:

sincostabell

Sabbad multiplikation

Rekommenderad från: 12 år

[kkratings]

På tavlan skrev matteläraren Adam en uträkning. Men precis innan lektionen skulle börja, så busade någon utav eleverna och bytte ut två siffror mot nya. Därefter stod det:

$4\cdot5\cdot4\cdot5\cdot4=2247$

Men vilka var siffrorna från början? Förklara hur du kommer fram till svaret.

Visa lösningen

Kenken och set

För den som tröttnat på Sudoku och Battleships vill jag föreslå ett par andra pussel.

Den första är kenken, ett spel som självaste Gunnar Berg spenderar timmar med! Till synes liknar pusslet sudoku, men man får inte lika många siffror utsatta från början. Det gäller att fylla tabellen så att siffrorna inom varje rad respektive kolonn är olika (siffrorna skall vara från 1 till tabellens storlek). Dessutom skall olikaformade rutor ge ett visst resultat med given operation. Står det 15+ till exempel, så ska siffrornas summa i området vara 15.

Det pusslet är lite roligare än sudoku tycker jag. Man får öva på lite fler tekniker. Det bästa man kan göra för att lösa pusslet är att tillämpa den så kallade flaskhalsprincipen. Man börjar med den platsen, där det finns så få möjligheter som möjligt. Till exempel, står det 4x i ett område innehållande två rutor, så vet man att talens produkt skall vara lika med 4. Men eftersom de står på samma rad/kolonn så är enda möjligeten talen 1 och 4 (men man vet inte än i vilken ordning de kommer). Man lär sig lite om olika sådana exempel för varje aritmetisk operation. Prova på själv!

Den andra spelet är Set, som i original pappersversion kan spelas med flera personer. Det gäller så snabbt som möjligt att hitta en trippel med kort som följer regeln ”allt lika eller allt olika”. Alltså varje egenskap som korten kan ha (färg, form, antal, fyllning) ska den i en set antingen vara lika för alla kort eller vara olika för alla kort. En annan tumregel är: ”om två är något, men inte den tredje, så är det inte ett set”. Det brukar vara svårt att hitta ett set i början, men efter ett tag utvecklar man ett sorts ”seende” och kan snabbt hitta de rätta korten. Spelet passar exakt lika bra för vuxna som barn.

Grisarna och kexen

Rekommenderad från: 13 år

[kkratings]

Vargen bjöd hem de tre små grisarna och Rödluvan för att titta på film. Efter att de var klara gick Vargen till köket, räknade alla kex och upptäckte att det saknades två. Men han har en stor balansvåg hemma som han kan använda. Hur kan med hjälp av två vägningar bestämma, vem som åt upp kexen? Alla kex väger lika mycket, alla grisar (i alla fall när de precis hade kommit till Vargen) också. Vargen vet även att Rödluvan bantar, så hon kunde max äta upp ett kex.

grisar

Visa lösningen

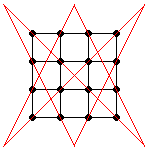
Överstrykning med sex streck

Rekommenderad från: 10 år

[kkratings]

Rita sex streck, så att alla 16 punkter på bilden blir överstrukna, utan att lyfta pennan från pappret och utan att strecken går längs med rutnätet.

vecka36

Visa lösningen

Mattebloggen

Fast på gräsmattan

Rekommenderad från: 14 år

Plan för staden med torg

Rekommenderad från: 12 år

Fyra färger räcker

Rekommenderad från: 14 år

Spiken i lådan

Rekommenderad från: 11 år

Tvåpotensens sista siffra

Rekommenderad från: 15 år

Svar:

moduloräkning

delbarthetsprincipen för 3

delbarthetsprincipen för 9

Lösning 1 (den officiella):

Lösning 2 (den med perioder):

Lösning 3 (den snygga):

Minnesregler för trigonometri – del 1

Sabbad multiplikation

Rekommenderad från: 12 år

Lösning:

Kenken och set

Grisarna och kexen

Rekommenderad från: 13 år

Diskussion:

Lösning:

Överstrykning med sex streck

Rekommenderad från: 10 år