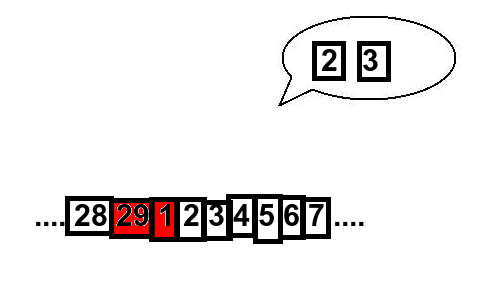Rekommenderad från: 15 år
[kkratings]
Tag en vanlig kortlek med 52 kort. Säg att kortleken ligger snyggt, ifall varje par av kort där ena ligger på den andra antingen har samma färg eller samma valör, samma sak gäller för det översta och nedersta kort samt att spader ess ligger överst. Visa att antalet sätt att lägga kortleken snyggt är
(a) delbart med 12! (12 fakultet, det vill säga 12*11*10*9*8*7*6*5*4*3*2*1)
(b) delbart med 13! (13 fakultet)

Ska man plugga matte själv eller i grupp?
Studierna på universitetet skiljer sig mycket ifrån gymnasiestudier. Det kan verka först att det enda som förändrats är mängden arbete man måste utföra för att klara sig bra, men så enkelt är det inte.
Mängden ”plugg” som måste ske är lika stor som på gymnasiet egentligen, men all planering lämnas nu åt dig själv. Det viktigaste under din första termin är att utveckla din studieteknik, det vill säga när, hur och var du pluggar för att lära dig bäst. Själv insåg jag detta så sent som mitt andra år på universitetet. Sedan dess har jag provat med olika sätt att plugga och bara nyligen (femte år på universitetet) kommit fram till hur jag pluggar bäst. Så sätt igång och utveckla din studieteknik nu!
Här är ett länktips:
Min favoritblogg i studieteknik (på engelska)
Ditt sätt att studera måste förstås anpassas efter ämne, låt oss anta att ämnet du skall studera är matematik. Du kanske redan har testat att öppna matteboken själv och upplevt hur långsamt det går att ta sig igenom texten. Det går att räkna några uppgifter själv men man fastnar alltid så småningom!
Annat är det om man har kompisar att plugga med! Alla hjälps åt att första det svåra i boken och om alla räknar samma uppgift så går det att jämföra svaren.
Det kan ofta avgöra dina studieresultat ifall du hittar någon person som det passar bra att plugga med. Hittar du någon som ligger på ungefär samma nivå som du, ungefär lika snabb på att räkna och som inser saker du inte gör och vice versa, blir det plötsligt mycket roligare att även tentaplugga. Kan personen passa tider, så kan det knappast bli bättre.
Men akta dig från att fastna i tankesättet ”det viktigaste är att klara tentor”. Det är inget fel med att tycka så egentligen och då rekommenderar jag delvis gruppräkning. Men vill du ha garanti på att du verkligen har lärt dig sakerna i en viss kurs, så måste du plugga huvuddelen av tiden på egen hand. Problemet med att vara i en grupp är att bilden av vad du egentligen förstår kan bli ganska skev. Kompisarna kommer inte vara där på tentan och kan inte fylla i dina luckor!
I matten finns ingen ”delförståelse”. Antingen förstår man en teori eller en metod eller så gör man inte det, vilket kan både vara nackdel och fördel. Visst, du kanske kan utföra en metod utan att förstå det och det ger absolut poäng på tentan, men du kommer inte minnas metoden sen. Poängen med kurser förutom faktakunskaper är framförallt att du ska ha sett strukturer och metoder, fått en känsla för dem och ska kunna känna igen liknande saker senare.
Det är precis på samma sätt med saker som vi lär oss i grundskolan. ”Vem bryr sig om spansk grammatik?” tänker man kanske, och har en helt berättigad fråga. Spansk grammatik är säkert inte så viktigt just för dig, men övar du på att förstå grammatiska strukturer kommer du ha det lättare när du lär dig nya språk, programmeringsspråk och andra saker senare i livet.
De senare åren på högskolan blir det för det mesta eget arbete. Kurserna har få deltagare, projekten blir fler. Därmed är det viktigt att du redan vet hur du testar dina kunskaper på egen hand, hur du tar dig igenom en svår bok eller uppgift. Glöm inte att föreläsarna och deras medhjälpare finns till för att svara på dina frågor, men tänk någon minut själv på frågan innan du ställer den. Tyvärr så är inte alla föreläsare perfekta, så det är bra att ha backup-planen ”studera själv” om du råkar få en dålig lärare, eller kursare som du inte vill plugga med för den delen.
Så plugga själv och diskutera frågor om du måste, och gör det helst med någon som kan ämnet. Pluggar du med kompisar är det bäst för dig själv att lära ut saker du redan kan för att minnas dem, men kom ihåg att någon annans förklaring implicerar inte din förståelse.
Ödlornas läsning
Rekommenderad från: 13 år
[kkratings]
Vi människor läser vanligtvis från vänster till höger och uppifrån och ner. Ödlor är inte lika snabba på att läsa, men de kan göra det på fler olika sätt. Ödlan kan läsa en bokstav och sedan förflytta sig ett steg ner, upp, till höger eller till vänster för att fortsätta läsa.
På hur många sätt kan en ödla läsa ordet FJÄRIL här nedan?

Spel på en remsa
Rekommenderad från: 15 år
[kkratings]
Det finns en rutig remsa 1xn:
Anders och Filip spelar ett spel. De turas om att göra drag: Anders får sätta ett kryss i en tom ruta och Filip får sätta en ring i en tom ruta. Dock får inte två kryss hamna bredvid varandra och inte heller två ringar. Spelaren, som inte kan göra ett drag när det är hans tur, förlorar.
Anders gör det första draget. Vem har ett vinnarstrategi, det vill säga vem kan alltid vinna oavsett hur motståndaren spelar?
Observera att svaret kan bero på talen n, som säger hur lång remsan är.
Tehuset
Rekommenderad från: 13 år
[kkratings]
55 indier och turkar träffades på ett tehus. Varje person drack antingen te eller kaffe. När en indier dricker te så talar hen alltid sanning och när hen dricker kaffe så luras hen alltid, medan turkarna är precis tvärtom. På frågan ”Dricker du kaffe?” svarade 44 personer ”ja”, ”Är du en turk?” svarade 33 personer ”ja” och på frågan ”Regnar det ute?” svarade 22 personer ”ja”. Hur många indier drack te på tehuset?

För svåra lektioner
Eleverna stirrar i tomma intet, läraren kan inte komma på tillräckliga förklaringar, alla lyssnar intensivt men ingen tar emot vad som sägs. Vad ska man göra när lektionen har blivit för svår? Och finns det någon poäng med att ha svåra lektioner?
För några få människor kan det vara väldigt stimulerande att gå på obegripliga föreläsningar. ”Tänk att det finns så mycket kvar att lära sig” inser de och blir stimulerade till att jobba mer för att ha chansen att första sådana framtida föredrag. Sådana människor har oftast inga problem att lära sig nya saker själva, eller i alla fall har lätt för stimulans för inlärning. Men för de flesta är det tyvärr inte så.
Sådana tillfällen då deltagarna tar till sig alldeles för lite för att kalla det hela ”förståelse” hör inte hemma i den vanliga undervisningen. Antalet träffar är mycket begränsat både i grundskolan och högskolan och man måste utnyttja dem maximalt. Det finns sätt att få i både stimulans, utmaning och förståelse i lektionen utan att göra det för svårt.
Hur gör man då som lektionsledare? Ofast har man (förhoppningsvis) större kunskaper än eleverna och därför också överskattar vad de har koll på och hur lätt det är för dem att förstå någonting nytt. Jag håller därför lektionerna på enklaste möjliga nivån, vilket innebär att jag alltid påminner om vad begrepp innebär. Som man säger på ryska ”Repetitionen är lärandets moder”. Ingen vågar ju ställa frågor om de enklaste sakerna, eller sakerna man gick igenom förra gången, för att inte verka dum. Men det är ju egentligen konstigt att förvänta sig att alla ska kunna allt man gått igenom. Men tyvärr tror de flesta att det är kravet för att vara duktig i skolan.
Det är ungefär som att förvänta sig att när en matematiker definierar någonting, så ska vi genast förstå det. Vadå, han har ju definierat det, det måste vara nu universiellt vedertaget :)
De bästa lektionerna jag har haft har varit interaktiva, där eleverna är så mycket som möjligt involverade i diskussioner och problemlösning men samtidigt bara då lektionen började på ganska enkel nivå. Det gäller att få igång dem och sedan öka svårighetsgraden långsamt.
En hel del svåra lektioner har jag haft också. Även om man gör det hela så enkelt som möjligt är det ingen chans att man gör det för enkelt men fortfarande stor chans att man gör det för svårt. Det är inte lätt att bryta mitt i lektionen och börja om, men det ger mer för klassen om man går igenom få saker ordentligt och begripligt än att man hinner igenom all tänkt material men tar sig igenpm det för fort.
Vad ska man gör som elev då? Om du upptäcker att du knappt förstår någonting på din lektion eller föreläsning, fråga om den första saken du inte förstod. Om svaret inte klargjorde något, gå därifrån. Antingen kunde inte läraren anpassa sig till din nivå eller så är du inte redo för att förstå ämnet eller så fungerar inte lärar-elev-relationen just på den lektionen. Hur som helst kommer du inte få ut särskilt mycket av att stanna kvar och det är då bättre att studera timmen ut på egen hand.
Ett matematiskt korttrick
Rekommenderad från: 12 år
[kkratings]
En trollkarl med förbundna ögon och hans assistent utför följande trick. Trollkarlen har 29 kort med talen 1 till 29 på. Han ger korten till någon person i publiken, som väljer ut två av dem. Resten av korten ges till assistenten, som sedan väljer två av de resterande korten och visar till personen i publiken. Personen läser upp högt båda talen för trollkarlen (i vilken ordning han vill). Därefter gissar trollkarlen vilka kort som personen valde ut i början.
Hur skall trollkarlen och assistenen förbereda sig för att alltid lyckas med tricket?

Att täcka över en svart kvadrat
Rekommenderad från: 10 år
[kkratings]
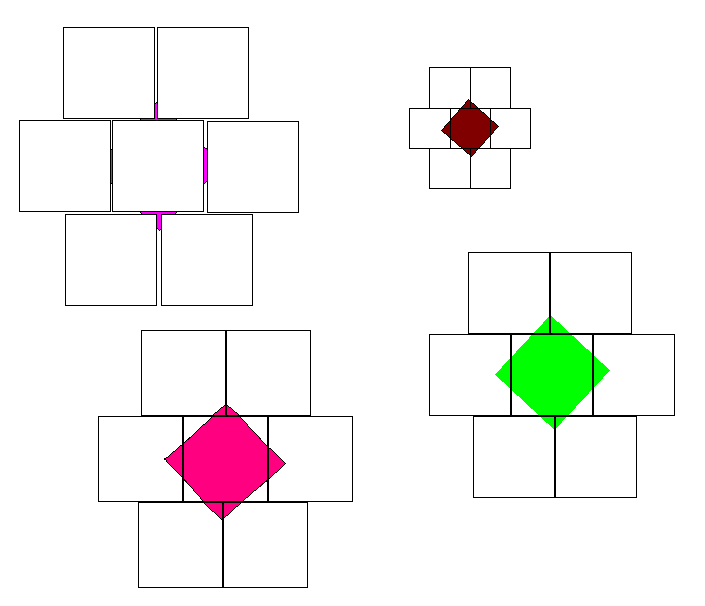
På ett papper finns en bild på en svart kvadrat. Du har tillgång till 7 kvadratformade brickor av samma storlek som den ritade kvadraten. Hur ska du göra för att täcka över kvadraten med brickorna så att inga brickor ligger på varandra och varje bricka täcker åtminstone en liten del av kvadraten (åtminstone en punkt inuti)?

Mattecirkel: lektion i logik
Första mötet med matematisk logik är för många påståendet ”Jag ljuger”. Det är förstås en paradox, eftersom någon som talar sanning, kan inte påstå att han ljuger. Och tvärtom, någon som ljuger, kan inte tala sanning om det. (Egentligen menas påståendet ”Jag ljuger just nu” här.)
Sådana här logikkluringar är perfekta för nybörjare i matematik. Det är klart och tydligt att någonting antingen kan vara falskt eller sant. Därför är uppgifterna nedan väldigt bra exempel på hur matematiker i allmänhet resonerar. Man lär sig vad matematiskt ”eller” och ”implikation” betyder som en del av språket för bevisredovisning och inte som formella symboler.
Dessutom har logikuppgifter fördelen att deras formuleringar inte alls låter som matte. De ges med fördel till barn som har matteallergi. Berätta då inte att det är matematik innan de satt igång!
Exempel på problem från mattecirkeln:
1. Magdas katt nyser alltid ett dygn före regn. Idag nös katten. ”Det kommer regna imorgon”, tänkte Magda. Har hon rätt?
2. `Kristian har fler än 1000 böcker”, sade Bodil.
”Nej, han har mindre än 1000 böcker”, sade Calle.
”Minst en bok har han säkert”, sade Emil.
Om bara ett av påståenden är sant, hur många böcker kan Kristian ha?
3. En gång blev Robinson tillfångatagen av en vild stam. Deras hövding sade: ”Enligt seden måste du uttala ett påstående. Om det blir sant ska vi äta upp dig. Om det blir osant ska vårt tama lejon äta upp dig.” Vad måste Robinson säga?
4. I ett land finns endast tre städer: Sannholm, Löngeborg och Turmö. Sannholmsborna talar alltid sanning, Löngeborgarna ljuger alltid och de som bor i Turmö turas om strängt att tala sanningar och lönger.
En dag såg en jourhavande brandsoldat en rök och telefonen ringde. ”Vi har en brand! ” ”I vilken stad brinner det? ” ”I Turmö ”. Till vilken stad skall brandkåren?
Uppdelning i nästan lika heltal
Rekommenderad från: 15 år
[kkratings]
På hur många sätt kan man skriva talet 2009 som en summa av några positiva nästan lika heltal? Talen kallas nästa lika om deras skillnad är (till beloppet) maximalt 1. Sätten betraktas som samma om det enda som skiljer dem åt är ordningen på termerna.
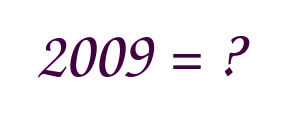
© 2009-2025 Mattebloggen

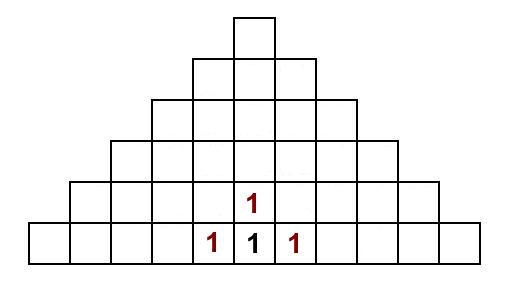 Om vi nu ska forsätta vandra till R:en, så kan vi hamna i vissa R från två olika I. Därför ska antalet sätt adderas där och vi får totala antalet sätt att läsa LIR och sluta i ett specifikt R. Just här är det kanske inte så svårt att räkna dem sätten från början, men metoden blir mer användbar senare:
Om vi nu ska forsätta vandra till R:en, så kan vi hamna i vissa R från två olika I. Därför ska antalet sätt adderas där och vi får totala antalet sätt att läsa LIR och sluta i ett specifikt R. Just här är det kanske inte så svårt att räkna dem sätten från början, men metoden blir mer användbar senare: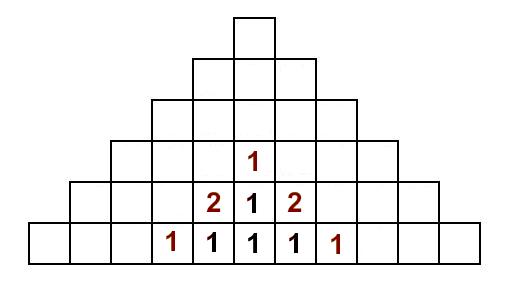 Forsätt att fylla ut tabellen på det sättet. Varje nytt tal blir summan av talen som kommer ”precis innan”, till exempel på höger sida blir det summan av talet under och talet till vänster (om nu båda finns). Till slut fås tabellen:
Forsätt att fylla ut tabellen på det sättet. Varje nytt tal blir summan av talen som kommer ”precis innan”, till exempel på höger sida blir det summan av talet under och talet till vänster (om nu båda finns). Till slut fås tabellen: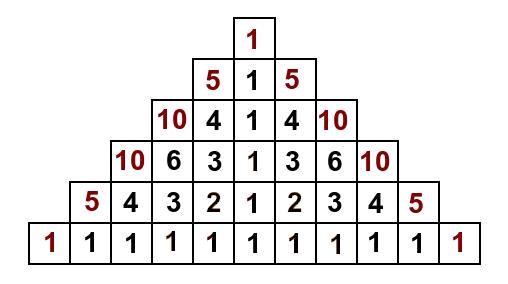 Återigen, antalet sätt totalt att läsa ordet LIRÄJF är 1+5+10+10+5+1+5+10+10+5+1=63.
Återigen, antalet sätt totalt att läsa ordet LIRÄJF är 1+5+10+10+5+1+5+10+10+5+1=63. eller
eller De fortsätter spela under tillåtna regler (aldrig två kryss eller två ringar bredvid varandra). Låt oss säga nu att Filip på något sätt lyckas förlora. Det betyder att han i en viss situation har ingenstans att sätta sin ring och de har precis varit Anders tur.
De fortsätter spela under tillåtna regler (aldrig två kryss eller två ringar bredvid varandra). Låt oss säga nu att Filip på något sätt lyckas förlora. Det betyder att han i en viss situation har ingenstans att sätta sin ring och de har precis varit Anders tur.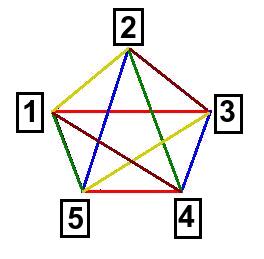
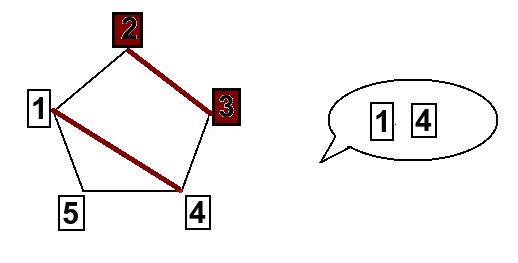 Till exempel så är följande kanter bruna: den som binder ihop 2 & 3, samt den som binder ihop 1 & 4. Ifall assistenten ser att åskådaren plockar bort korten 2 och 3, så pekar han på korten 1 & 4 och trollkarlen kan då komma ihåg att kanten 1 & 4 hade den bruna färgen och säga exakt vilka kort som plockades bort från början (de som också hade den bruna färgen).
Till exempel så är följande kanter bruna: den som binder ihop 2 & 3, samt den som binder ihop 1 & 4. Ifall assistenten ser att åskådaren plockar bort korten 2 och 3, så pekar han på korten 1 & 4 och trollkarlen kan då komma ihåg att kanten 1 & 4 hade den bruna färgen och säga exakt vilka kort som plockades bort från början (de som också hade den bruna färgen).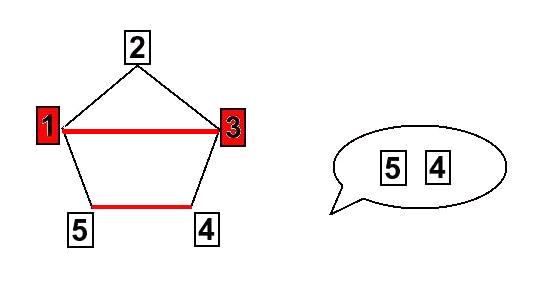
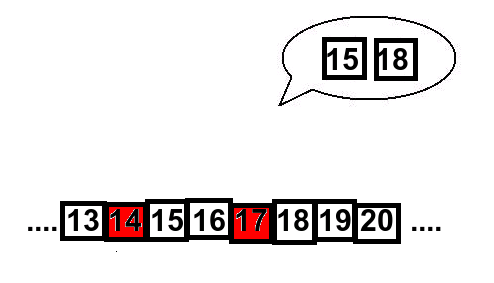 Om de valda korten ligger bredvid varandra, så pekar assistenen på två kort som också ligger bredvid varandra, nämnligen de två som kommer direkt efter. Här är ett exempel:
Om de valda korten ligger bredvid varandra, så pekar assistenen på två kort som också ligger bredvid varandra, nämnligen de två som kommer direkt efter. Här är ett exempel: