Rekommenderad från: 15 år
[kkratings]
En dag bestämde sig en snigel för att starta en resa. Snigeln rörde sig framåt längs med en rak sträcka i 6 minuter tills det var nog för dagen. Under den tiden kom några människor och tittade på snigels underbara resa. Hela tiden var snigeln betraktad av åtminstone en människa. Det visade sig att varje människa kollade på snigeln i exakt 1 minut och under den tiden kröp den exakt 1 meter. Hur mycket kunde snigeln maximalt krypa under den dagen?
Förtydliganden: För det första så betraktade varje människa snigeln bara under resans gång. För det andra, så kollade varje människa på snigeln 1 minut i sträck och inte utspritt hur som helst.
Idén är att utnyttja tiderna maximalt: snigeln rör sig jättefort när bara människa kollar på den. Annars, om det inte är start- eller slutminut, så står snigeln stilla (och vilar). Klart!What the Best College Teachers Do
Även om man har ett riktigt jobb, ett rätt krävande sådant, så har man ibland lite tid att läsa böcker också. En dag såg jag en bok med titeln ovan liggande hemma hos min vän. ”Jag vill vara en sådan!” tänkte jag, ”hur gör man?” och bad om att få låna boken. Det var någon gång i november tror jag.
Boken, som är skriven av Ken Bain, tog ett tag att läsa, för att engelskan i den är lite svår. Jag läste klart den igår (mars är det nu). Men redan från början blev jag helt fascinerad av idéerna och ofta la jag undan boken för att tänka igenom hur jag skulle kunna implementera vad som står där. Jag kan lugnt säga att det till en jättestor del var just den här boken som fick mig att starta bloggen.
Vad kan man säga om boken? Det är en studie där många framstående universitetslärare betraktades och man såg vad de gjorde för saker gemensamt. Det är väldigt läsvärda insikter, oavsett om man är lärare eller elev. Det framgår tydligt att undervisningens poäng är att hjälpa människor att lära sig saker och hjälpa dem att lära sig hur man lär sig själv saker. Om man förstår hur man bäst lär sig då lär man sig bättre, givetvis!
Ett av de viktigaste insikterna jag kom fram till om mig själv hade att göra med min uppväxt. Barn, som får uppmuntran och beröm för specifika saker de utför, lär sig att hårt och inbitet arbete lönar sig. Andra, som får beröm i största allmänhet, tror snarare på att intelligens är medfött och olika talanger kan inte uppkomma eller utvecklas från ingenting. Individerna i det senare fallet tycker snarare om att jobba med saker som är lätta att klara av och senare på universitet bryr sig inte så mycket om djup inlärning. Jag insåg med lite ångest att jag var ett av de senare fallen till en stor del. Nu tror jag på att hårt arbete ger resultat oberoende av hur bra man var på något från början.
Vad finns det mer att säga om boken? Läs den!
Och ifall ni har några andra böcker om undervisning som ni kan rekommendera, skriv det gärna i kommentarerna!
Svenska eller engelska?
Imorgon skall jag hålla i en föreläsning om kategoriteori. Det är i en kurs som några doktorander går, och varje deltagare måste hålla i ett par föreläsningar själv. Vilket är jättebra, tycker jag, för man lär sig bäst genom att berätta materialet för andra, men det blir kanske ett annat inlägg.
Det som förbryllar mig ibland är att på de avancerade matematikkurserna sker undervisningen i princip alltid på engelska. Det beror ibland på utbytesstudenter närvarande, eller kanske gästforskare från utomlands, men ofta är inte fallet så. Ofta kan alla i rummet prata svenska, förstå svenska på ett bättre nivå än engelska (för de flesta får minst lika mycket praktik i svenska). Ändå föreläser man på engelska och diskuterar eventuell frågor på engelska också.
Det finns en enkel orsak till det, nämligen att det inte finns någon utvecklad terminologi i avancerad matematik på svenska. Hur säger man ”pullback”, ”sesquilinear” eller ”Lie bracket”? I talspråk doktoranderna emellan säger man ”Liebracketen”. :) Det är inte helt uteslutet att de svenska orden finns, men de är i vilket fall inte i bruk. Läser man matematiklitteratur på engelska, så kan man orden just på engelska och inget annat.
Vari ligger problemet då?
Jo, även om det känns onaturligt att prata engelska i ett rum full av svensktalanade personer, så är inte det ett fel i sig. Men, majoritetn av de här personerna talar mindre flytande engelska än svenska. Säg att någon ska ställa en fråga. Då går halva (eller mer) tankekraften åt att formulera frågan på engelska och resten åt att tänka igenom matematikinnehållet i frågan. Språk och matematik ockuperar samma hjärnhalva och slåss om hjärnkapaciteten!
Efter att frågan är ställd, skall en annan svensktalande person först uppfatta frågan, översätta och tolka den matematiskt och sedan händer samma process med svaret. Det är inte problematiskt i sig att diskussionerna pågår långsammare, men man tappar det här flytet, så att det hela inte längre går att kalla för ”ett naturligt samtal”.
Händer detta på en grundutbildningskurs är det ett ännu värre problem, eftersom många har svårare för att ställa frågor då. Jag vågade i alla fall inte prata engelska förrän sista året på utbildningen.
Nu har jag mycket mindre problem med engelskan, men jag vet inte om jag borde köra på det imorgon för terminologins skull. Jag menar, vem är inte van att höra på föreläsningar på svengelska ;)
Dela upp en lägenhet
Rekommenderad från: 12 år
[kkratings]
En lägenhet består av ett antal rum som kan ha olika areor. Det går att dela lägenheten mellan 2, 3 eller 4 hyresgäster så att varje person får bo på samma area (fast antalet rum kan vara olika). Bestäm det minsta möjliga antalet rum i en sådan lägenhet.
Mattecirkel med Anna: lektion 1
Jag har precis börjat mattecirkeln med Anna, en elev som nu går i nian i Uppsala.
Det är många som frågat mig vad ”mattecirkel” egentligen betyder, för det känns kanske lite dumt att kalla någonting för ”cirkel” när bara två personer träffas. Men jag väljer det namnet av en gammal vana, och för att det är en sorts studiecirkel oavsett hur många som kommer.
Mattecirklar är en gammal tradition i Ryssland och en ganska ny i Sverige. I de flesta fall är det träffar med några stycken elever, som kan ungefär lika mycket matte, och en lärare. Varje sådant tillfälle tar 1-2,5 timmar, lite beroende på elevernas åldrar.
Dessutom för att få lite struktur på det hela brukar lektionerna ha en genomgående tema. Kanske att det handlar om trianglar eller kanske om induktionsprincipen. Målet är att eleven ska förstå en viss idé och prova lite på tekniken genom att lösa problem ur en lista.
Här är lite smakprov vad Anna sysslade med i lördags, temat var ”Uppskatta och ge exempel”. Alla problem kräver förstås förutom svar också motivering. Vill ni ha fler problem från lektionen (de nedan är de lättaste), så är det bara att maila till mig eller skriva i kommentarerna.
Att bevisa
Idag startar min nya mattecirkel. Det är förvisso bara en elev i den än så länge, men jag kallar det hela mattecirkel i alla fall av en gammal vana. Mina mattecirklar brukar innehålla sådana problem som inte förekommer i vanliga skolan, utan snarare i matematiktävlingar, som HMT.
Det är svårt men ganska spännande att introducera någon till matematikvärlden. Vilka områden skall man lära sig mer om först av allt? Vilka problemlösningstekniker?
Det mest essentiella i matematikstudier är att kunna avgöra vad som är ett bevis eller inte. Sedan så småningom får man intuition för vad som är tillräckliga bevis eller inte. Till exempel blir studenter ganska ofta osäkra på ifall de kan anta ett visst påstående i kursboken eller om man ska visa påståendet. Eller hur många Gausseliminationer måste man redovisa för att uppgiften inte ska få avdrag?
Allt detta beror på i princip på erfarenhet, och man lär sig att avgöra sådana frågor efter några månader eller något år.
Hur började du med matematiken? Vilka bevis förstod du först av allt?
(Passande förresten att starta en mattecirkel på pi-dagen :) Grattis alla!)
Linjär avbildning
Jag ska försöka reda ut begreppet linjär avbildning. Det är trots allt det linjär algebra i stort sett handlar om.
För det första är linjär avbildning synonymt begrepp med linjär transformation, och båda varianterna används flitigt. Detta tyder på att det är något aktivt som sker, någonting avbildas eller någonting transformeras.
Något förändras helt enkelt. Men inte hur som helst!
För att ta exempel ur vardagen: att ta ett foto på ett vackert landskap är en linjär avbildning från naturen till kameraskärmen. Tänk dig att en linje dras mellan varje pixel och motsvarande ”punkt” i naturen. På något sätt kan vi tänka oss att det är en jämn och regelbunden hopknutning av linjer.
En avbildning som däremot inte är linjär är när någon ritar skämtteckning föreställande dig. Den är ju helt fel! Försöker man tänka sig linjer på samma sätt som i förra exempel, så blir de huller om buller.
Det är därför just linjära avbildningar studeras så mycket, dels för att de är vackra och regelbunda, dels för att de är (just därför) mycket enklare än godtyckliga transformationer.
Nu till seriösa avbildningar. Den formella definitionen för att F skall vara en linjär avbildning är att den uppfyller två saker:
Detta betyder att en linjär avbildning bevarar förhållanden mellan punkter, som ligger på en och samma linje utgående från origo. Som jag ritade linjerna på bilden med landskap så menade jag att origo skulle vara i övre vänstra hörnet. Dra en ”origolinje”, till exempel linjen som går från hörnet genom den högsta bergstoppen och in i solen. Det här villkoret säger oss att avståenden från hörnet till toppen och från hörnet till solen förhåller sig på samma sätt (med samma faktor) både i den lilla och i den stora landskapsbilden.
Det andra villkoret är lite svårare att förklara med en bild. Här ska man föreställa sig en massa vektorer (utgående från origo). Det måste alltid gälla att när vi tar två sådana vektorer och kollar på vad de avbildas på, så blir de två nya vektorer som dock också utgår från origo. Tar man summan av de ursprungliga två och summan av de senare två så ska dessa resultat hänga samman med precis samma avbildning. Det vill säga första summan avbildas på den senare summan.
Linjära avbildningar är mycket mer generella grejer än det först verkar. Det beror på att så kallade vektorer är väldigt generella objekt i sig. De behöver inte vara ”pilar i planer” eller ”pilar” överhuvudtaget. Vektorer kan vara matriser, funktioner, tal, … katter (om man vet hur man summerar två katter för att få en annan katt, samt hur man multiplicerar katter med skalärer).
Därför är det rätt svårt att kolla om villkoren 1 och 2 stämmer geometriskt. Oftast får man avbildningen genom en formel och då är det bara att ”stoppa in” och visa att vänsterledet är lika med högerledet för att möjliga indata (vektorer) och skalärer (konstanter) a.
Det finns många kända exempel på linjära transformationer som är bra att känna till. Att derivera funktioner är ett sådant exempel (slå upp deriveringreglerna och hitta två av dem som liknar våra villkor väldigt mycket). Att integrera funktioner är ett annat. Att multiplicera med en fixerad matris är en linjär avbildning också och många avbildningar representeras just på det sättet.
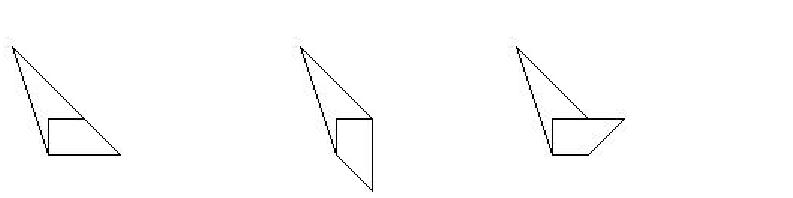
Sist, men inte minst, kommer lite linjära avbildningar från planet till sig självt:
Här ligger origo alltid i ”ursprungliga övre högra hörnet”, det vill säga det hörnet där solen är närmast.
Två fyrkanter
Rekommenderad från: 12 år
[kkratings]
Rita två fyrkanter, som tillsammans kan läggas ihop till
(i) En triangel, men också en femkant
(ii) Både en triangel, en fyrkant och en femkant.
Med ”läggas ihop” menas att fyrkanterna inte får överlappa varandra, inte heller får det bildas hål.
En liten inluppsrättningshistoria
I stort sett varje lärare spenderar många timmar av sitt liv på att rätta tentor och inlämningsuppgifter. Det kan vara frustrerande, om många personer gör olika fel. Det kan vara snabbt och lätträttat när alla gjort rätt. Men ofta är det tyvärr tråkigt, när det gäller inluppar i alla fall, nämligen att studenterna har samarbetat och gjort exakt likadana fel.
Under en sådan session berättade min kollega om ett roligt avskriftsfel.
Uppgiften gick ut på att hitta en bas till något rum, det vill säga en lista med vektorer. Svaret bestod alltså av en uppradning av vektorernas koordinater.
Min kollega håller på och rättar uppgiften. I en av inlupparna har en viss elev gjort allting rätt, men plötsligt kommer det någonting konsigt på slutet. Precis på raden med svaret är det fel! Av någon anledning har eleven delat alla vektorer med 5. Hmm, men allt annat är ju rätt, så varifrån kommer det här konstiga felet, tänker min kollega … Ett tag senare hittar han en annan elev, som har gjort precis samma fel! Allt är rätt, men vektorerna delas med 5 på slutet.
Då detta uppenbarligen varit avskriftfel letar min kollega igenom högen efter originalet. Vad ser han där? Allt i uppgiften är gjort rätt. Och på slutet, så har eleven markerat svaren lite grann, genom att stryka under varje vektor. Ni vet, sådan s-formad understrykning. :)
Moralen är: det märks oftast när studenterna skriver av varandra utan att tänka efter.
Alternativa examinationsmetoder: munta
Det finns många olika sätt att genomföra sin undervisning. Läraren kan ha föreläsningar, lektioner, laborativa pass, case studies och diskussionstillfällen, bara för att nämna några. Men det många inte tänker på är att man också kan variera sig när det gäller slutlig examination.
Det man oftast väntar sig av en kurs i ett teoretiskt ämne, är att den slutar i något form utav skriftligt prov. Ibland är det en så kallad hemtenta, det vill säga ett större prov man skriver hemma på egen hand. Men oftast är det en salstenta, men begränsad tid och bestämda frågor, vars svar skall lämnas in skriftligt av var och en.
Denna examinationsform är dominerade och det är inte så konstigt varför det är så. Men hjälp av några skriftliga frågor och problem går det att täcka det mesta av kursinnehållet. Dessutom finns det äldre prov som man kan basera sina egna på. Då finns det två föredelar: eleverna studerar gamla tentor och vet de vad de har att förvänta sig av det nya, samt att läraren kan vara säker på att ta upp allt det relevanta.
Eller?
Det går aldrig att testa om en elev kan allt innehåll i kursen och man kan argumentera om vad ”kan” egentligen betyder. Men det gör vi inte här. Istället vill jag berätta om mina erfarenhet av muntlig examination!
När jag och några kollegor ordnade munta var det inte den enda stora examinationen, utan en del av det. Om man klarade muntan behövde man inte göra en svår del av tentan. Detta var alltså ett sätt att locka studenterna till att göra munta. Varje munta beräknades ta 10 minuter per student och man fick komma i grupper om max 3 personer (dock inte hjälpa varandra med att svara på frågorna under muntans gång). Allt för att göra det hela till en behaglig upplevelse.
Själv hade jag aldrig behövt göra munta under min tid på universitetet. Och hade jag behövt göra det skulle jag ha varit rädd, speciellt första gången. Kan man inte allting utantill känns det inte jättelockande att spendera ens 10 minuter med lärarna som ställer frågor och ber en berätta allt möjligt och bli bedömd på direkten. Kanske till och med utskrattad! Hemskt!
Trots allt detta kom majoriteten av våra elever, läste på innan dess, gjorde sitt bästa under muntan och var i stort sett nöjda med hela experimentet efteråt. Vi ställde för det mesta teoretiska frågor om envariabelsanalys. De fick formulera satser, ibland bevisa något eller lösa något exempel på tavlan. Eleven fick själv välja ett ämne inom anaysen att berätta om, och vi lärarna valde ett annat ur en lista med ämnen (som var känd innan).
Vi hann givetvis inte prata om så mycket med eleven på 10 minuter, men i någon mening blev det i alla fall något som påminde om en dialog. Eleven har chansen att försvarar sig om denne blir missuppfattad, samma gäller oss lärarna. Det var också en fördel att vara flera stycken som diskuterade betyget (eleven fick inte vara med då, men vi var alltid två lärare). Det var inte bara den rena kunskapen vi betygsatte utan också förmågan att berätta matematik för någon annan och kunna uttrycka sina tankar.
För är inte det som är målet med alla våra kurser egentligen? Den faktiska kunskapen spelar sekundär roll, förståelsen kommer med tiden. Det mesta i kursen är ändå inte särskilt viktigt att kunna i ens framtida yrke. Att kunna förklara sina tankar däremot är en av de mest grundläggande färdigheterna som behövs för framgång!