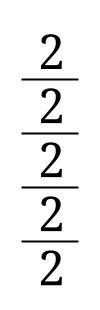Bråkuppställningen på bilden är lite konstig, eftersom det inte går att tyda vad som ska delas med vad i vilken ordning. Du får göra bråkstrecken olika långa för att kunna räkna ut resultatet.
Hur många olika resultat går det att få på det sättet? Vilka är de möjliga svaren?
Att dra olika långa bråkstreck innebär att vi bestämmer ordningen på divisionerna, vilket är samma sak som att sätta ut parenteser i uttrycket 2/2/2/2/2 (som annars inte har ett bestämt sätt som det ska räknas ut på).
Vi kan börja med att sätta ut parenteser för att bestämma vilken division som ska räknas ut sist:
2/(2/2/2/2)
eller
(2/2)/(2/2/2)
eller
(2/2/2)/(2/2)
eller
(2/2/2/2)/2
Notera att de sista två möjligheterna är de första två ”vända upp-och-ner”. Det betyder att om vi kan få ett resultat genom de första två uträkningarna, så kan vi få 1/resultat genom någon av de sista två, om man ritar bråket likadant, fast upp-och-ner vänder strecken. Så vi betraktar bara de första två fallen.
2/(2/2/2/2) eller 1/(2/2/2) är alltså det som gäller om vi redan nu räknar ut täljaren (2/2) i det andra fallet.
Det näst största bråkstrecken (den näst sista divisionen) i fall 1 kan sättas ut på olika sätt:
2/(2/(2/2/2)) = 2*(2/2/2)/2 = 2/2/2
eller
2/((2/2)/(2/2)) = 2/(1/1) = 2/1 = 2
eller
2/((2/2/2)/2) = (2*2)/(2/2/2) = 4/(2/2/2)
och från fall 2 har vi fortfarande
1/(2/2/2)
Parenteserna i uträkningen (2/2/2) kan sättas ut på två sätt: 2/(2/2) eller (2/2)/2. I första fallet blir värdet 2 och det andra 1/2. Det sätter vi in i alla möjligheterna ovan:
2/2/2 ger 2 eller 1/2
2 ger bara 2
4/(2/2/2) ger 4/2 och 4/(1/2) alltså 2 eller 8
1/(2/2/2) ger 1/2 och 1/(1/2) alltså 1/2 eller 2
Så allt som allt fick vi resultaten 1/2, 2 och 8, men glöm inte att vi kan få de inverterade resultaten genom att vända helt på bråken. Detta ger resultaten 2, 1/2 och 1/8, så bara det sista är nytt.
Så totalt finns 4 möjliga uträkningar på bråket: 1/2, 2, 8 och 1/8.