Mattegåta
Martin samlar på ovanliga mynt. Mynten i hans samling alla har en diameter på högst 10 cm. Samlingen förvarar han i en låda som har storlek 30 cm x 70 cm (i ett lager, inga mynt ligger ens delvis ovanpå varandra).
Men nyss fick Martin ett nytt mynt med en diameter så stor som 25 cm. Visa att den nya samlingen får plats i en låda som är 55 cm x 55 cm stor (också nu i ett lager).
Diskussion
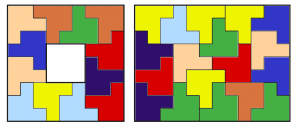
Uppgiften handlar lite om att optimera. Om vi har eventuell platsbrist i den nya lådan, så är det nog lite dumt att lägga det stora 25 cm x 25 cm-myntet i mitten utav den. Mycket smartare är det att lägga det i ett hörn.
Mynt kan även ligga på krångliga sätt, de är ju cirklar av olika storlekar. I varje mellanrum går det att stoppa in ett pyttelitet mynt till. Därför är det omöjligt att uppskatta antalet mynt och även hopplöst att försöka omplacera mynten för mycket.
Så gissningsvis ska mynten ligga ungefär som de gjorde i första lådan. Och det stora myntet ska ligga i ett hörn. Dessa två antaganden leder fram till lösningen nedan.
Lösning (av Benjamin Fayyazuddin-Ljungberg)
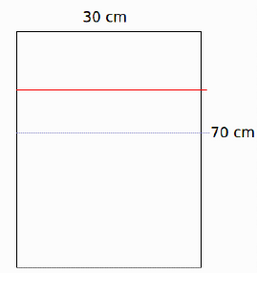
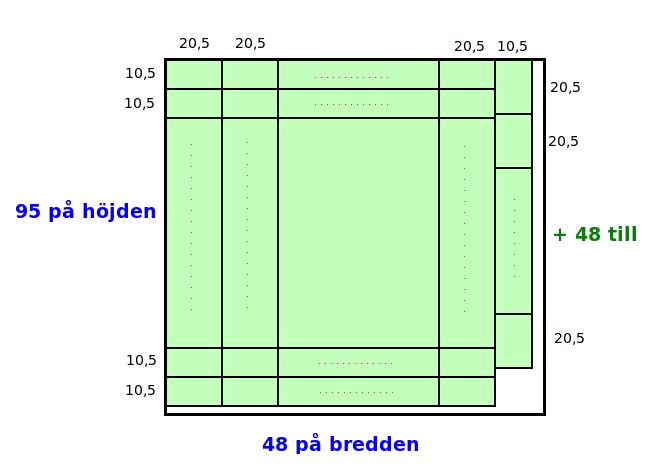
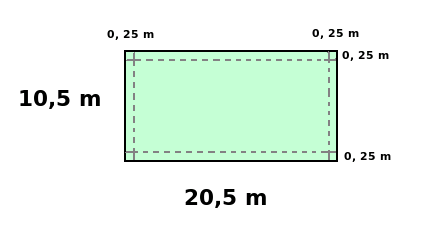
Rita ett rött streck 15 cm in på Martins ursprungliga låda, så att den delas in i två delar av storlek 30cm*55cm och 30cm*15 cm. Rita ett parallellt blått streck, 10 cm längre in än det röda, så att vi får två delar av storlek 30cm*45cm och 30cm*25cm.
Dela in lådan två (överlappande) rutor, ett som begränsas uppifrån av överkanten på lådan och nedifrån av det blåa strecket (storlek 30cm*25cm), och ett som begränsas uppifrån av det röda strecket och nedifrån av nederkanten på lådan (storlek 30cm*55cm).
Eftersom mynten högst har diameter 10 cm kan det inte finnas något mynt sådant att det röda strecket och det blåa strecket båda passerar genom det. Därför kan vi säga att varje mynt tillhör den rutan som helt innefattar det myntet. Alla mynt tillhör då någon ruta, och får plats i den. Det kan finnas mynt som hamnar i båda rutorna, då kan man godtyckligt välja vilken ruta de ska tillhöra.
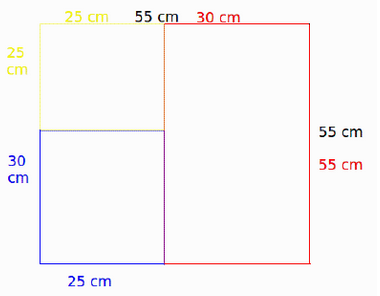
Nu flyttar vi runt rutorna, med alla tillhörande mynt, och placerar dem i Martins nya låda. Vi ser då att vi får plats med en gul ruta i hörnet med storlek 25cm*25 cm. Alltså får det nya myntet plats också.