Etikett: roten ur 2

Matteklubben är Uppsala kommuns satsning på begåvade elever i matematik. Jag har äran att förbereda aktiviteterna som vi håller på med och vara en av lärarna. Du kan kolla upp var vi gjorde på första träffen och andra träffen innan du läser vidare.

Många lärare

Till Matteklubbens träffar kommer cirka 30 elever och antalet lärare brukar bli ungefär en på 5 elever. Några frågar mig vad alla lärare utom mig gör och jag brukar svara att de verkligen behövs! Det finns alltid saker att göra: Allt från att dela ut pennor och fika till att delta i matematiska diskussioner med de mest envisa eleverna. Det är väldigt bra att vara fler än en lärare, är man ensam så kan man göra något grovt matematiskt fel och det är inte säkert att någon upptäcker det. Det gör ingenting om en lärare har fel, men det är viktigt att reda ut felen. Eleverna måste se att det är sanningen i matematiken som gäller, och inte lärarnas subjektiva (och möjligen något auktoritära) åsikter.

Hemuppgiften

Lektionen började med läxan, precis som förra gången. Den hade ingen gjort så det blev en klassdiskussion.

Först undersökte vi vad som hände med en figur vars sidor blir hälften så stora. Hur många gånger mindre blir arean? En elev förklarade att om man tänkte på en kvadrat, så såg man att den gick från att vara fyra rutor till att bara vara en. Därmed kunde man se att arean blev fyra gånger så liten.

Den andra uppgiften var (är och förblir) riktigt svår, så jag ställde en ledande fråga till klassen. Det var en uppgift vi hade förra gången, om hur man kan rita en kvadrat med dubbel så stor area som en given. Det vill säga, rita en kvadrat på ett rutat papper med arean lika med exakt två rutor.

Många elever föreslog att man skulle förstora varje sida 1,5 gånger. En elev hade kollat upp med sin pappa att sidan i målkvadraten är roten ur 2, det vill säga ungefär 1,4. Båda förslagen vände jag mig emot med argumentet att det då inte blir en exakt bild (och arean blir inte heller exakt 2). Och om sidorna förstoras 1,5 gånger visade min kollega på tavlan att arean faktiskt blir större än 2. Det visade sig i diskussionen med kollegan senare att de gamla grekerna tänkte på precis samma felaktiga sätt som barnen på Matteklubben, de ville också förstora sidorna med 1,5.

Jag gav ledtråden om att en ruta består av två trianglar. Hur kan man rita en figur som består av dubbelt så många trianglar? En eller två av eleverna kunde då rita en korrekt bild på tavlan, det vill säga en vriden kvadrat, där sidorna utgörs av rutdiagonaler. Jag poängterade att denna figur har exakt dubbelt så stor area som en ruta.

För att lösa läxans andra uppgift tipsade jag om att kombinera svaren på uppgifterna vi har diskuterat hittills. Man ska egentligen tänka på samma sätt som i problemet där en kvadrat ska få dubbelt så stor area.

Grafteori

När man är nybörjade på matematisk problemlösning, vet man inte alltid hur uppgifter kan börja lösas. Det gäller då att visa upp många olika verktyg för barnen, för att de ska kunna välja det som passar vid varje tillfälle. Tillsammans med eleverna skapar vi en schweizisk armékniv med problemlösningstekniker. Men det är viktigt att inte behöva övertala dem (vilket ofta sker på vanliga mattelektioner) om att en viss teknik är viktig och kommer troligen att användas ”senare”. Istället väljer jag uppgifter där en viss teknik uppstår naturligt, och man ser direkt hur det underlättar problemlösandet.

En sådan teknik går utt på att rita scheman över objekt som finns i problemet, det som på högnivå-mattespråk kallas ”att rita en graf”.

Uppgifterna

Vi hade bara tre uppgifter på temat, men det var ganska mastiga alla tre. Många hann lösa ettan och börja på tvåan, men trean hann jag knappt diskutera med någon grupp.

Under uppgifterna står vanliga dialoger som skedde på lektionen.

1. I vår solsystem finns 8 planeter och Pluto, som en gång i tiden räknades som planet. Man utvecklade rymdturismen genom att erbjuda följande rutter (både fram och tillbaka): Jorden-Merkurius, Pluto-Venus, Jorden-Pluto, Pluto-Merkurius, Merkurius-Venus, Uranus-Neptunus, Neptunus-Saturnus, Saturnus-Jupiter, Jupiter-Mars, Jupiter-Neptunus, Mars-Uranus.

(a) Går att ta sig från Jorden till Mars?

Vissa elever missade ”fram och tillbaka” och vissa var lite osäkra på vilka planeter man fick åka emellan (det vill säga om man fick ”mellanlanda”). När vi redde ut dessa saker kunde de fortsätta med problemet.

Elever: Svaret är ”ja”….eller ”nej”… kanske… vi vet inte riktigt.
Lärare: Om det går, hur skulle man gå tillväga då? Hur skulle man exakt åka, mellan vilka planeter?

Elever: Svaret är ”nej”, för om man tar sig till Mars måste man komma från Uranus eller Jupiter, och om man ska ta sig till Jupiter så är det från Saturnus eller Neptunus, och till Neptunus kommer man från Jupiter så det går inte.
Lärare: Men ni har inte missat några utvägar då? Har vi verkligen kollat alla möjligheter? För att vara säkra så kan ni rita ett schema lite som scheman nedan.

(b) Vilka av scheman nedan kan representera ruttsystemet?

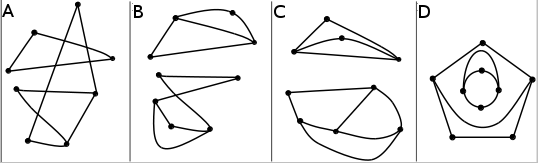
(c) Finns någon planet på schemat som du med säkerhet kan ange namnet på?

Uppgifterna (b) och (c) diskuterade jag med hela klassen ståendes framme vid tavlan. Några elever fick komma fram och rita egna scheman, samt säga vilka av scheman på bilden som fungerade för uppgiften. Eleverna kunde även korrekt förklara att man kunde bestämma Saturnus, men inga andra planeter. Rättare sagt, tillsammans kunde de exakt bestämma vilka villkor gällde för Saturnus (kopplad till två planeter, som båda är kopplade till tre planeter). Många kunde även förklara varför det inte gick att bestämma andra planeter med säkerhet.

2. Några barn i klassen kan spela olika musikinstrument: Pia kan spela gitarr och piano, Ville kan spela gitarr och dragspel, Tommy – fiol och cello, Daniel – bas och trumpet, Lena – piano och dragspel, Sara – fiol och trumpet, Solveig – cello och bas. På hur många sätt kan man ge var och en av dem ett instrument (alla instrument måste vara olika) så att alla kan spela samtidigt?

Elever: Vi ritade ett schema och såg att varje barn var kopplad till två instrument och varje instrument spelas av två barn.
Lärare: Kan man rita schemat på något annat sätt så att det ska bli lättare att bestämma svaret i uppgiften?

Elever: Vi gjorde en tabell och skrev upp alla möjligheter. Det blev fyra.
Lärare: Är ni säkra på att ni inte missade några möjligheter?

Även denna uppgift gick jag igenom på tavlan för att visa exempel på hur man ”snyggar till” scheman. Tricket är att inte bara rada upp instrumenten på ena raden och barnen på andra raden och sedan börja koppla ihop dem. Istället kan man börja med ”gitarr-Pia-piano” och sedan fortsätta med nästa person som ska spela piano och vidare göra så tills cirkeln är sluten. Då får man ett mycket tydligare schema. Jag visade att det då var självklart att ena cirkeln kunde fördela instrumenten på två sätt och andra också på två.

Vad blev svaret då? ”Fyra”, svarade barnen. ”Två plus två eller två gånger två?” undrade jag. Många av barnen förstod inte riktigt hur jag menade (”Det är ju samma sak!”). Men när jag förklarade att om det hade varit 2 och 3 sätt i respektive cirkel, skulle jag då addera eller multiplicera dem, så förstod många att det var multiplikation jag var ute efter. Kul att visa att 2+2 och 2*2 inte ”betyder” samma sak. Återigen, att det är hur man tänker, och inte svaret, som räknas.

3. I ett höghus med 100 våningar finns en hiss, som bara har två knappar: ”+7” och ”-9”. Den första knappen får hissen att gå upp sju våningar, den andra får den att flytta sig 9 våningar ner. Går det att åka:
(a) Från första våningen till den andra?
(b) Från den andra våningen till den första?

En del elever hann nosa in på den här uppgiften och lösa (a) och möjligen (b) också. De som var klara fick kika på hemuppgifterna, där de ofta fortsatte med hissuppgiften. Se nästa inlägg för fler detaljer.

 

Regatta

Andra delen av lektionen genomförde vi en liten tävling, matteregatta. Regattan var planerad i tre omgångar, men vi hann bara med två, och dessutom fick vi korta ner den andra omgången till 10 minuter.

Elevernas delade sig själva upp i par och sedan sattes paren ihop till lag om fyra. Vissa lag fick vara tre personer. Alla lag fick heta någon frukt som till exempel lag Ananas (för att inte slösa bort tid på att hitta på lagnamn gav jag alltså ut lagnamnen). Sedan fick de för första gången öva på att skriva ner lösningar på Matteklubben (och inte bara berätta dem). Juryn, vilket var de andra lärarna, satte poäng på lösningar som de hade fått in.

Efter att eleverna var klara med första omgången, gick jag igenom lösningarna, medan juryn rättade. Därför kan jag inte säkert säga varför poängen blev som det blev, annat än att juryn bedömde fullständighet och korrekthet. När omgången var rättad, fick alla höra poängen samtidigt som att de fick möjligheten att protestera över sin poäng. Då är tanken att juryn går igenom lösningen en gång till och kollar efter om lösningen eventuellt är värd mer poäng.

Tanken med den demokratiska aspekten är återigen att minska auktoritetens betydelse och ta bort eventuell objektiv bedömning från matematiken. Det är som till slut är värt poäng är resonemanget som finns nedskrivet på pappret, och inför det står alla lagen lika.

Vi fick dra över tiden lite grann för att på samma sätt hinna gå igenom andra omgången. Om du är intresserad av riktlinjerna som juryn hade vid rättningen, så kan du ladda ner dem här nedan.

 

 

Resultat

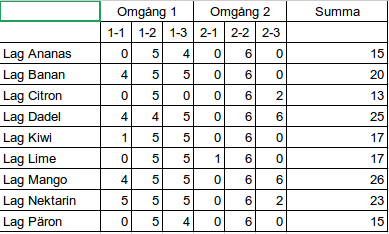
Här är regattans fullständiga slutgiltiga resultat. Grattis återigen till lag Mango som vann i en jämn kamp!

Tankar efter lektionen

Efter lektionen samlades vi alla lektionsledarna för att diskutera vad som har gått bra och dåligt. Vi var som vanligt imponerade av elevernas förmåga att ta åt sig nya idéer. Det kändes också att lektionens uppgifter blev bra (lagom svåra och roliga).

Det som man hade kunnat göra bättre var att ha ett tydligare schema, som eleverna och lärarna skulle försöka hålla sig till. Det hade varit bra bland annat för att hinna med den inplanerade tävlingen. Lektionen kändes också något stökigare än vanligt och där skulle fasta tider ha hjälpt. Det var bra med rast tyckte alla lärare!

Det ska bli spännande att träffa eleverna en sista gång innan Jullovet. Då blir det också dags för utvärdering!