Ett enkel spel med tärningar
Rekommenderas för
Förskolan, lågstadiet, mellanstadiet
Materiel
Ett spelplan (skriv ut nedan), två vanliga sexsidiga tärningar (helst av olika färger), minst 4 pjäser (från ”Fia med knuff” till exempel)
Tid
15 minuter
Antalet deltagare
2+
Regler
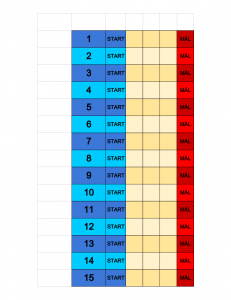
Reglerna är enkla: alla spelarna turas om att sätta ut sin pjäs på något av ”START”-fälten. Bara ett pjäs får stå på varje sådant fält. Det är viktigt vilket fält man ställer sin pjäs på, ställer man bredvid 10 till exempel, så blir 10 pjäsens tal.
Om man är två, tre eller fyra spelare är det bra om alla har minst två pjäser var. Alla kan till exempel sätta ut sin första pjäs, en i taget, och sedan sätta ut den andra pjäsen i omvänd ordning, för att det ska bli så rättvisst som möjligt.
Sedan är dags för själva racet. Man turas om att slå två tärningar, och beroende på vad summan av prickarna blev får en pjäs eventuellt gå fram ett steg (oavsett vem som slog tärningarna). Till exempel, om tärningarna visar summan 3, så är pjäsen som startade vid 3 den som får gå ett steg åt höger. Om ingen pjäs startade vid 3, så får ingen pjäs heller gå fram något.
Den som vinner är spelaren vars pjäs först kommer in i mål, det vill säga den pjäsen som först gick fyra steg fram. Man kan också köra tills tre pjäser kommer in i mål och på så sätt ha en etta, en tvåa och en trea. Bestäm själva beroende på hur ”segt” spelet går.
Naturligvis är det mest intressant att köra flera omgångar!
Vad barn upptäcker själva
Utan att man berättar något annat än reglerna upptäcker barnen några saker själva:
1. Det är dumt att ställa sin pjäs på 13,14,15 och inte heller 1, för den summan kan aldrig visas på två tärningar.
2. 12 och 2 är inte heller så bra tal, för de kommer rätt så sällan.
3. Det är nog bäst att ställa i mitten, på 6-8 nånstans (och det är i princip alltid en av de pjäserna som vinner).
4. Allt det blir så, beror på att det finns många kombinationer det kan bli 7 på (1+6, 2+5, 3+4, 4+3, 5+2, 6+1 ses tydligast om tärningarna har olika färger), men färre på de andra talen.
Som sagt, man säger inte ord, och barn utför matematiskt tänkande själva! Undervisning när den är som bäst :)
Skriv ut ett spel själv
Ladda ner pdf:en med ett färdigt spelplan.
(sidan 
ligger precis under sidan 
). Föreställ er att finns en liten tetraeder 
som är gjord av ett annat material. Vi kommer att följa den tetraederns position allt eftersom tärningen rör sig.
hade från början, fast parallellfärflyttad. Och vice versa, 
på sidan 
, men den sistnämnda ligger utanför tetraedern av annorlunda material. Motsägelse.