Bussar på vägen
Lars går längs med en väg med konstant hastighet. Var 6:e minut ser han en buss som åker förbi honom och var 3:e minut möter han en buss som åker åt andra hållet. Bussarna åker med samma fart åt båda håll och startar från ändhållplatserna med jämna mellanrum. Hur långa är dessa mellanrum?
Skolsteg
Skolsteg
Maria, Jakob och deras pappa går till skolan tillsammans. Under tiden som pappa tar 3 steg, så tar Maria 5 steg. Under tiden som Maria tar 3 steg, så tar Jakob 5 steg. Maria och Jakob räknade till att de tog 400 steg till skolan tillsammans. Hur många steg tog deras pappa till skolan?
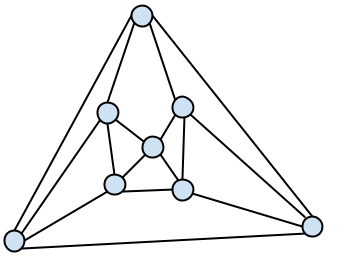
Ett land utan korsningar
Ett land utan korsningar
[kkratings]
I ett sagoland finns 8 städer. Från varje stad leder 4 vägar och inga vägar korsar varandra. Rita kartan över landet genom att beteckna städerna med punkter och vägarna med sträckor.
Fram och tillbaka igen
Fram och tillbaka igen
[kkratings]
Från by A till by B leder en enda väg som är 15 km lång. Klockan 9:30 började en hob promenera med hastigheten 4 km/h från A till B. Nästa dag startade han klockan 11:00 från byn B och gick tillbaka till A med hastigheten 5 km/h. Båda dagarna gick hoben över en bäck som korsar vägen vid exakt samma klockslag.
Vilket klockslag var det han gick över bäcken?
Tre påsar med mynt
Rekommenderad från: 13 år
[kkratings]
Du har tre påsar med hundra mynt i varje. I en av påsarna väger alla mynten 9,9g, i en annan väger alla 10g och en tredje väger alla 10,1g, men du vet inte vilka mynt som ligger i vilken påse. Du har även en våg som kan visa den exakta vikten, men går sönder om du lägger på mer än 50g på den. Hur kan du med en vägning bestämma vilka sorts mynt ligger i varje påse?

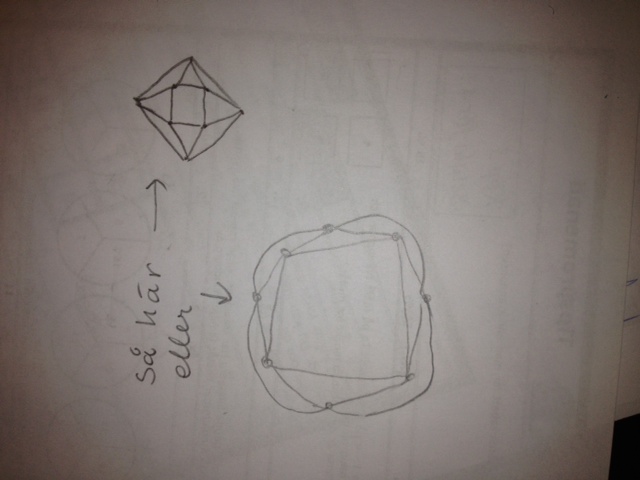
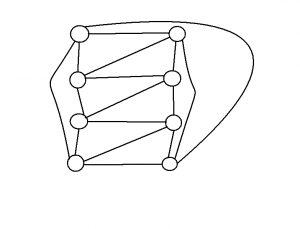
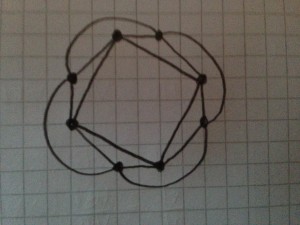
En kung som gillade att bygga
En kung som gillade att bygga
[kkratings]
I Sagolandet fanns en kung som tyckte mycket om att bygga. En gång bestämde han sig för att bygga 6 torn och anlägga vägar mellan varje par av torn, men på så sätt
att det bara skulle bildas tre korsningar mellan vägarna. Dessutom fick bara två vägar mötas i varje korsning, aldrig fler.
Hur skulle planen över tornen och vägarna kunna se ut?
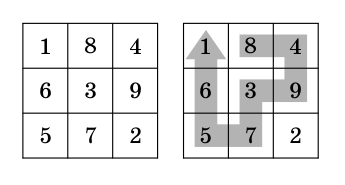
Pilen
Rekommenderad från: 10 år
[kkratings]
Siffrorna 1 till 9 fyller kvadraten som det syns på den vänstra bilden. Man får gå på kvadratens rutor, men aldrig tillbaka till en ruta man varit på förut, och man måste alltid gå till en angränsande ruta.
Katarina gick längs med pilen som syns på den högra bilden. Hon skrev ner siffrorna som hon gick på i ordning och fick talet 84937561. Rita en annan väg, som ger ett större tal (ju större tal, desto bättre).
Spänd tråd
[kkratings]
I en vägg sitter tjugo spikar (se bilden). Avståndet mellan två spikar som sitter precis bredvid varandra är 1 cm.

Din uppgift är att spänna en 19 cm lång tråd mellan spik 1 och spik 2, så att den går igenom alla spikarna. Hur gör du?
Problem vecka 19
Uttrycket (3 poäng).
Man utvecklade uttrycket (x+y)^n med hjälp av binomialsatsen. Den andra termen i summan blev lika med 240, den tredje blev lika med 720 och den fjärde blev lika med 1080. Hitta x, y och n.
Ön (7 poäng).
a) På en platt cirkelformad ö finns 4 hamnar (i den ordningen): 1, 2, 3 och 4. Mellan dem finns vägar där det kan finnas korsningar, det vill säga punkter där vägarna möts, korsas eller grenas. På alla sträckor är trafiken enkelriktad, på så sätt att man aldrig kan komma tillbaka till en hamn eller korsning om man startar därifrån. Låt fij beteckna antalet vägar som går från hamn i till hamn j.
Visa olikheten f14f23≥f13f24
b)
Visa att om det finns 6 hamnar (1, 2, 3, 4, 5, 6 i den ordningen) så gäller
f16f25f34+f15f24f36+f14f26f35≥f16f24f35+f15f26f34+f14f25f36
Visa lösningar
© 2009-2025 Mattebloggen