Nyligen hölls SM i matte för gymnasister, som kallas Skolornas Matematiktävling. Tävlingen bestod av 6 uppgifter som eleverna fick lösa under 5 timmar.
De officiella lösningarna har inte kommit upp än, så jag tänkte föreslå egna. Samt kommentera på vad du kanske gjorde fel, om du deltog.
VARNING: det är inte säkert att lösningarna är fullständiga enligt de kriterierna som juryn sätter upp. Men enligt mig är de det :)
Problem 1
Längs en lång vandringsled finns markeringar för antalet passerade kilometer efter varje kilometer, med början vid starten där det står markering 0. En vandrare som börjar gå vid vandringsledens start ägnar sig åt att räkna siffrorna i dessa markeringar. Hur många kilometer har vandraren gått vid den kilometermarkering som innehåller den 2013:e siffran?
Lösning
Här gäller det att vara nogrann. Många tankefel och räknefel kan uppstå!
Vi räknar ensiffriga skyltar för sig, de består av 10 siffror (siffrorna 0 till 9).
Vi räknar tvåsiffriga skyltar för dig, de består av 2*90 = 180 siffror (talen 10 till 99 är precis 90 stycken).
Räknar vi ihop tresiffriga skyltar, så kommer vi få ett tal som är större än 2013, så det är någonstans på ett tresiffrigt tal som den 2013:e siffran förekom.
2013 – 180 – 10 = 1823, det vill säga vi ska ta reda på 1823:e siffran bland de tresiffriga talen. Låt oss kolla hur många tresiffriga tal vandraren passerar innan han kommer till siffra 1823.
1823/3 = 607 rest 2, det vill säga vandraren passerar 607 tresiffriga tal och det eftersökte talet är det tresiffriga talet nummer 608.
Det tresiffriga talet nummer 1 är 100, nummer 2 är 101, osv. så talet nummer 608 är alltså 608+99 = 707. När vandraren har passerat skylten med talet 707, har han gått exakt 707 kilometer.
Fel
Förutom räknefel är tankefelet +-1 (”plus-minus-ett”) det vanligaste, då man kanske tänker att man börjar med skylten som det står 1 på eller att man betraktar det 607:e tresiffriga talet (iställer för det 608:e).
Problem 2
I en stad som ligger på gränsen mellan två länder kan man fritt använda ländernas respektive valutor daler och mark. Dag köar bakom två flickor och tre pojkar vid en biograf. Han noterar att flickorna betalar sina båda biljetter med en tiodalerssedel och får åtta mark tillbaka. Pojkarna betalar sina tre biljetter med en trettiomarkssedel och får nio daler tillbaka. Dag lyckas betala för sin biljett med jämna pengar genom att enbart använda endalersmynt och enmarksmynt. Hur många mynt av vardera slaget behöver han för detta?
Lösning
Här gäller det att införa bekväma beteckningar, samt förstå att endast svar räknas inte (jag tror att man måste motivera varför det endast finns ett alternativ).
Låt B vara biljettkostnaden, M beteckna en mark, D en dal. Då får vi ekvationerna:
2B = 10D – 8M
3B = 30M – 9D
Samt att B kan skrivas som en summa av ett helt antal M och helt antal D. Men hur?
Låt oss pyssla lite med ekvationssystemet och får bort B:n för att få veta hur D och M kan växlas mot varandra.
3*(2B) = 3*(10D – 8M)
2*(3B) = 2*(30M – 9D)
Så 30D – 24M = 60M – 18D och således 48D = 84M vilket förkortas med 12 till 4D = 7M.
Ur första (eller andra) ekvationen kan vi få priset för en biljett, men inte som en summa:
B = 5D – 4M.
Låt B = yD + xM = 5D – 4M (x och y är positiva heltal). Då gäller (x+4)M = (5-y)D och alltså även
7*(x+4)M = 7*(5-y)D. Här kan vi se att y < 5 för att högerledet ska vara positivt, liksom vänsterledet.
7M kan ersättas med 4D, alltså har vi:
(x+4)4D = 7(5-y)D och efter att förkortat med D får vi:
4*(x+4) = 7*(5-y), där allt är heltal. Vänsterledet är delbart med 4, således även högerledet. 7 är relativt primt med 4, så 5-y måste vara delbart med 4. Eftersom y < 5 är y = 1 det enda talet som passar.
Alltså har vi 4*(x+4)=28, så x=3. Därför är B = 3D + M och det är det enda sättet att uttrycka biljetten så som uppgiften beskriver.
Fel
Som sagt, efter lite prövning kan man få svaret B = 3D + M, men glömma att motivera varför det är det enda svaret.
Problem 3
Två koncentriska cirklar (det vill säga två cirklar med samma medelpunkt) har radier a och b, där b > a. Låt PQ vara en diameter i den större cirkeln. En linje genom Q tangerar den mindre cirkeln i punkten T. Bestäm längden av sträckan PT uttryckt i a och b.
Lösning
Det första vi gör är att rita en bild, förstås.
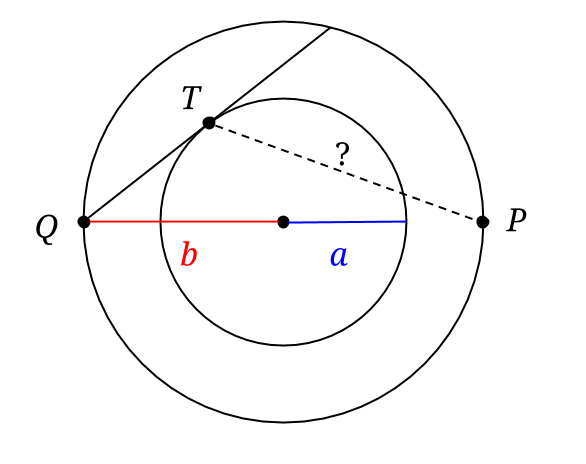
Eftersom den okända sträckan inte ingår i någon triangel, där vi känner till sidorna, ser vi till att dra extra linjer och benämna extra punkter:
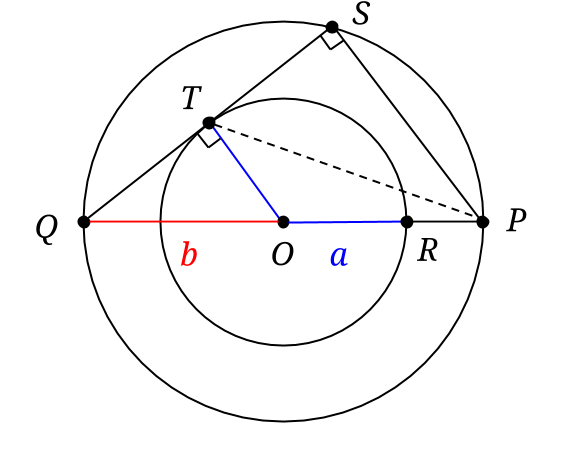
Vinkeln , eftersom det är en vinkel mellan radien till en tangent och själva tangenten (eller kan ses som en degenererad randvinkel). Vinkeln
eftersom det är en randvinkel på den stora cirkeln, som har diametern som bas.
Triangeln är alltså rätvinklig med hypotenusan
, en katet
och således den andra kateten lika med
enligt Pythagoras sats.
Triangeln är likformig med
eftersom båda är rätvinkliga, samt delar en annan vinkel. Likformighetskoefficitenten är 2, eftersom
, medan
. Det betyder att
och
.
Men då känner vi till kateterna i den rätvinkliga triangeln .
,
, så vi kan räkna ut
med Pythagoras sats:
Fel
Inte så mycket fel man kan göra här, man behöver knappast redovisa för några olika fall som kan uppstå när man ritar bilder. Alla värden och resonemang är desamma oavsett hur bilden exakt ser ut.
Problem 4
På ett papper har Ida på en rad skrivit 27 positiva heltal, ordnade efter storlek. Det första talet är 1 och det sista är 25. Ida berättar för Emil att summan av samtliga tal är 127, att summan av de nio första talen är 21, samt att summan av de nio sista talen är 65. Räcker den informationen för att Emil ska kunna avgöra vilket tal det är som står i mitten?
Lösning
Här räcker det att titta på talen från slutet. Vi får veta att de nio sista talen har summan 65. Eftersom det sista talet är 25, så är summan av de åtta näst sista talen lika med 40. Det innebär att det nionde talet från slutet är som mest 5, för hade det varit 6 eller större, slulle de åtta näst sista talen ha summa 48 eller större.
Det betyder alltså att de första arton talen är mellan 1 och 5. Låt oss bara tänka på dem nu. Talens summa är 127 – 65 = 62. Den sista halvan av talen (nio stycken) har summan 62 – 21 = 41.
Låt oss anta att det mittersta talet (som även är det mittersta talet i den stora bilden) är 4 eller mindre. Det betyder att det först kommer fem tal som är alla 4 eller mindre och sedan kommer det fyra tal som är som mest 5. Det betyder att summan av dessa nio tal är totalt 40 eller mindre. Motsägelse, eftersom summan är 41.
Det innebär att det mittersta talet är inte 4 eller mindre. Så det måste vara 5, det vill säga informationen räcker.
Fel
Här kan räknefelen ha avgörande betydelse. Det är ju precis på gränsen att talen räcker till en motsägelse, så att vi kan utesluta alla fallen utom talet 5.
Problem 5
Låt och
vara positiva heltal. Betrakta de
punkter med heltalskoordinater
som uppfyller att
, och
. Var och en av dessa punkter färgas i en av
, olika färger som är numrerade från 0 till
. I punkten med koordinater
ges färgens nummer av resten vid heltalsdivision av
med
. Om varje färg förekommer i lika många punkter, visa att minst ett av talen
och
är jämnt delbart med
.
Lösning
Ett av de största utmaningarna i uppgiften är att tolka vad som överhuvudtaget händer! Är man van vid koordinator och kvantorer, så förstår man så småningom att det handlar om en rektangel bestående av punkter i koordinatsysemet, där bredden består av punkter, medan höjden utgörs av
punkter. Det vill säga,
punkter per rad och
per kolonn. Totalt är det givetvis
punkter, vilket nämns i uppgiften.
Dessa punkter målas i färger på ett speciellt sätt. Nämnligen räknar man summan av punktens koordinater och sedan tar resten vid division med $k$ (och målar punkten i färgen med det numret). Till exempel, nedre vänstra hörnet har koordinaterna (0,0). Eftersom 0+0 = 0, kommer den punkten målas i färg 0. Punkterna (1,0) och (0,1) kommer målas i samma färg 1. Punkterna (2,0), (1,1) samt (0,2) kommer målas i samma färg 2 (om det finns så många färger). Men vänta nu, det verkar som att alla höger-nedåtgående diagonaler målas i samma färg, alltid!
Detta stämmer, eftersom koordinatsummorna på varje sådan diagonal kommer vara lika, således även resterna vid division med kommer vara lika. Detta stämmer eftersom neråt-höger från
ligger
. Med induktion får vi att alla punkterna på en sådan diagonal har samma färg som den vänstraste av dem, så allihopa har samma färg.
Eftersom det handlar om rester vid division med och diagonalsummorna ökar med 1 hela tiden (vi går från
till
), så betyder att färgerna ”börjar om” efter att
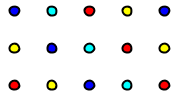
diagonaler målas. Så vi har följande bild för t.ex.
:
Det är givet att varje färg ska förekomma precis lika många gånger. Låt oss anta att varken eller
är delbara med
och komma fram till en motsägelse.
Om hade varit delbart med
, så skulle lika många punkter av varje färg förekomma på varje rad, eftersom
punkter i rad har de alla
olika färgerna (och sedan börjar cykeln om). Så låt oss ta bort den största delen från varje rad, som är delbar med
. Det vill säga, vi tar bort $b\cdotk$ kolumner. Kvar på varje rad blir en rest, som då är mindre än
(men större än 0). I den kvarvarande delen är det fortfarande lika många punkter av varje färg.
Låt oss nu tar bort lika många punkter av varje färg genom att förkorta kolonnerna på samma sätt. Vi kapar av den största biten, som är delbar med , från varje kolonn. Kvar blir en liten rektangel med storleken
, som fortfarande uppfyller reglerna, men vars bredd
och höjd
(räknat i antal punkter) är mindre än
.
Till exempel: om antalet färger är 4 och rektangeln hade storleken 10×7, så blir det en 2×3-bit kvar, eftersom 10 ger rest 2 vid division med 4, medan 7 ger rest 3.
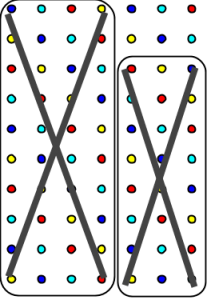
Vi kan lika gärna anta att övre vänstra hörnet i den lilla kvadrvarande rektangeln är målad i färgen 0 (annars döper vi om färgerna helt enkelt). Poängen är i alla fall att oavsett storleken på den lilla rektangeln, kommer färgen 0 förekomma exakt gånger, nämligen just den diagonalen som övre vänstra hörnet ligger på (den består utav
eller
punkter, beroende på vilket tal som är minst) och inga fler punkter.
Varför inga fler punkter? Jo, om någon rad eller kolonn innehåller fler punkter av en och samma färg betyder det att raden/kolonnen är minst punkter lång, vilket motsäger konstruktionen av den lilla rektangeln. Och vi vet att diagonalen med färgen 0 antingen går igenom alla rader eller alla kolonner (beroende på vilka som tar slut först).
Antag att (det finns fler kolonner än rader (eller så är deras antal lika)), och färgen 0 förekommer alltså
gånger). Hur många gånger förekommer då färgen
? Jo, det är som minst
gånger, eftersom precis så många punkter finns på diagonalen under den med färgen 0. Men det är inga fler punkter av den färgen heller. Av samma anledning som innan kan inte den finnas med på de raderna som redan innehåller färgen
. Det kan inte heller finnas på första raden, eftersom den raden börjar med färgen 0 och således måste innehålla minst
punkter för att färgen
också ska förekomma. Motsägelse. I det här faller har alltså minst två färger olika antal punkter.
Antag att gånger. Men med samma resonemang som ovan, måste färgen 1 förekomma
gånger och inga fler, eftersom den omöjligen kan finnas i första kolonnen. Även här har två färger olika antal punkter!
Vi har kommit fram till en motsägelse, det betyder att det inte kan finnas någon rektangelbit kvar när vi tar bort kolonner eller rader, vars antal är delbart med . Det betyder att antingen antalet rader eller antalet kolonner (eller båda) är ett tal som inte ger rest vid division med
, vilket skulle bevisas.
Fel
Felet man kan göra här är att tro att uppgiften går (dessutom) ut på att bevisa att OM åtminstone en utav och
är delbar med
så gäller att det finns lika många punkter av varje färg. Detta stämmer, och kan hjälpa en på vägen till lösningen, men det efterfrågas inte i uppgiften.
Ett annat fel i bevisföringen är att från påståendet att är delbart med
(om det finns lika mycket av varje färg, så måste antalet punkter vara jämnt delbart med antalet färger), dra slutsatsen att $a$ eller $b$ är delbart med
. Detta gäller bara om $k$ är ett primtal.
Problem 6
Punkterna P, Q, R är valda på sidorna BC, CA, AB i en triangel ABC på ett sådant sätt att P Q, QR, RP delar triangeln ABC i fyra likformiga trianglar. Visa att åtminstone två av dessa måste vara kongruenta (det vill säga likformiga och lika stora). Ge också ett exempel (med motivering) som visar att alla fyra inte behöver vara kongruenta.
Lösning
Problemet består alltså av två delar. Först, visa att två av de små trianglarna måste vara kongruenta. Och sedan visa att inte alla fyra trianglarna måste vara det. Då räcker det förstås att visa ett exempel då det inte är uppfyllt. Helt lätt är det inte att beskriva sådana exempel på ett korrekt sätt, men vi kommer till det.
Även om alla fyra trianglarna är likformiga, så sägs det inte vilka vinklar som förekommer på vilka positioner. Vi betraktar två stora fall: i det första är alla vinklarna hos de små trianglarna olika, medan i det andra fallet är (minst) två vinklar lika med varandra.
Markera ut de olika vinklarna hos mittentriangeln. För att slippa beteckna med bokstäver kallar vi de andra tre trianglarna för ”topp”, ”höger” och ”vänster”, medan de olika vinkelstorlekarna är grön, gul och lila:

Nu måste vi dela upp situationen i ännu fler fall. Vi kommer anta färgen hos en av vinklarna som gränsar med gul och efter det försöka härleda så mycket information som möjligt. Slutsatsen vi alltid kan dra i det här fallet är att eftersom summan av de tre olikafärgade vinklarna är 180 grader, så stämmer alltid att om två färger kompletteras med en tredje vinkel till en rät linje, så måste den tredje vinkeln ha den färgen som saknas (eftersom vinklarna har olika storlek). Notera att det inte stämmer att två vinklar av samma färg inte kan vara bredvid varandra.
Fall 1a. Låt oss anta att vinkel 1 är lila. Då är den kompletterade vinkeln grön. Nu måste vi göra ett antagande igen, och vi antar att vinkel 2 är gul:
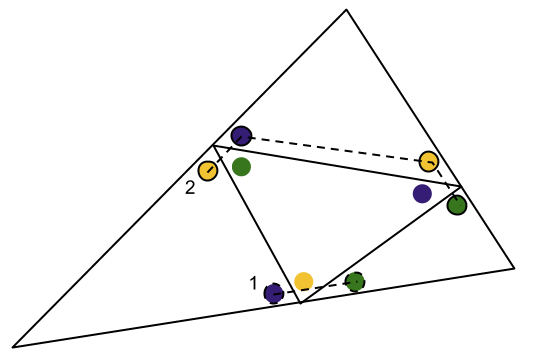
Följ den punkterade vägen från vinkel 2. Den kompletterade vinkeln är blå. Om vi antar att det INTE finns kongruenta trianglar bland de små, så måste nästa vinkel vara gul, annars skulle topp- och mittentriangeln vara kongruenta på grund av vinkel-sida-vinkel (blå, grön, samt den gemensamma sidan). Då är den kompletterande vinkeln grön och nu har vi två gröna vinklar i högertriangeln. Men den måste innehålla tre olika vinklar, motsägelse.
Fall 1b. Vinkel 1 är fortfarande lila och låt nu istället vinkel 2 vara grön.
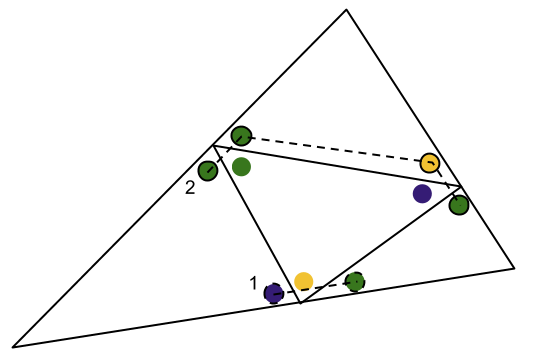
Den kompletterande vinkeln kan inte vara något annat än grön, eftersom annars skulle den räta linjen innhålla två olika färger, och alltså även tre olika. Men så är inte fallet. För att topp- och mittentriangeln inte ska vara kongruenta måste nästa vinkel vara gul. Då är kompletterande vinkeln grön och vi har samma motsägelse som förut.
Fall 2. Antag att vinkel 1 är grön.

Då är den kompletterande vinkeln förstås lila. Nästa vinkel är förstås grön på grund av icke-kongruens mellan mitten- och högertriangeln. Slutligen är den kompletterande vinkeln gul.
Gå åt andra hållet nu. Översta vinkeln i vänstertriangeln är lila, annars skulle mitten- och vänstertriangeln vara kongruenta. Den kompletterande vinkeln är gul och då har vi fått två gula vinklar i en triangel!
Fall 3. Antag att vinkel 1 är gul (jodå, det kan hända).

Så som vi har motiverat tidigare (fast med grön färg), måste den kompletterande vinkeln också vara gul (vilket för övrigt innebär att gul är lika med 60 grader). Nästa vinkel är grön på grund av icke-kongruens mellan mitten- och högertriangeln. Den kompletterande vinkeln är då gul.
Åt andra hållet, toppvinkeln i vänstertriangeln är lila, på grund av icke-kongruens mellan mitten- och vänstertriangeln. Då är den kompletterande vinkeln gul, och vi har fått en motsägelse.
Alltså måste i dessa fall alltid funnits två kongruenta trianglar.
Fall likbent. Av bekvämlighetsskäl har vi hittills inte betraktat fallet då några av vinklarna i en och samma liten triangel kan vara lika. Det är för att kunna föra resonemanget med de tre olika färgerna utan tvetydigheter (och för att få motsägelse snabbare). Vi betraktar separat nu fallet, då mittentriangeln har två gula vinklar och en grön (som kan vara lika med gul):
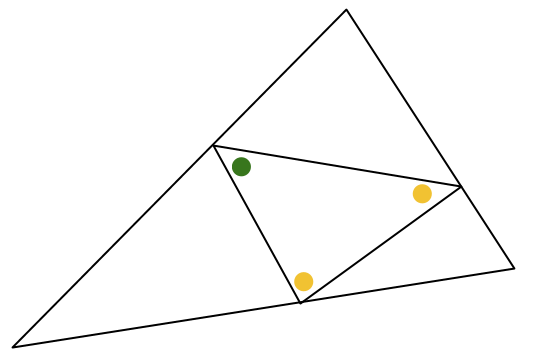
Då kan vinkel 1 antingen vara grön, men då kommer vi fram till att två trianglar måste vara kongruenta hur vi än försöker få dem att inte vara det:
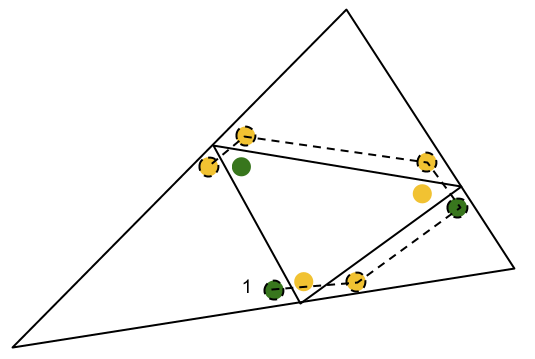
Och om vinkel 1 är gul, kommer vi fram till att högertriangeln måste innehålla två gröna vinklar. Det innebär att grön = gul och således är vilken triangel som helst kongruent med den i mitten.

Pust! Genom att betrakta fem olika fall visade vi att två av trianglarna måste vara kongruenta (notera att det alltid är mittentriangeln som är kongruent med en av de andra). Nu gäller det att konstruera en triangel där de fyra små trianglarna inte alla är kongruenta.
Som inspiration utgår vi från den här bilden, då vinklarna av olika färger är olika:
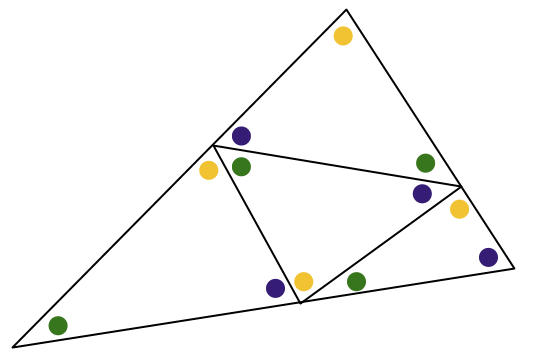
Topp- och mittentriangeln är kongruenta, men kan alla fyra vara det? I så fall har alla små trianglar samma längd på sidan som går mellan den gula och den gröna vinkeln. Vi markerar dessa fyra lika sträckor:
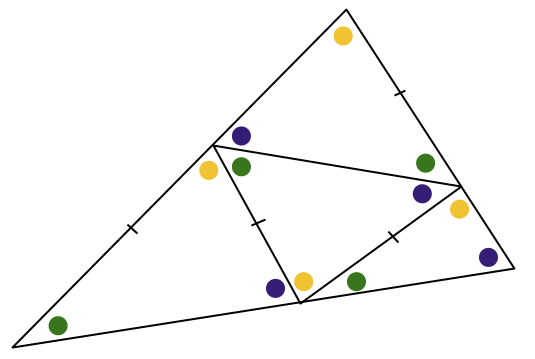
Men det innebär att till exempel mittenrektangeln är likbent och den gröna och den blåa vinkeln är lika. Motsägelse, eftersom vi antog de vara olika. Är vi klara då?
Inte riktigt, vi har fortfarande inte visat att inspirationsbilden är genomförbar. Kan vi konstruera en sådan bild om vi väljer tre olika vinkelmått, som tillsammans ger 180 grader (självklart finns sådana taltripplar)?
Vi utgår från topp- och mittentriangeln som tillsammans bildar en parallellogram. Vi fortsätter linjerna som ska bilda den stora triangelns vänstra samt högra sida. Kan vi nu rita undersidan på så sätt att vinklarna blir så som vi vill ha dem?
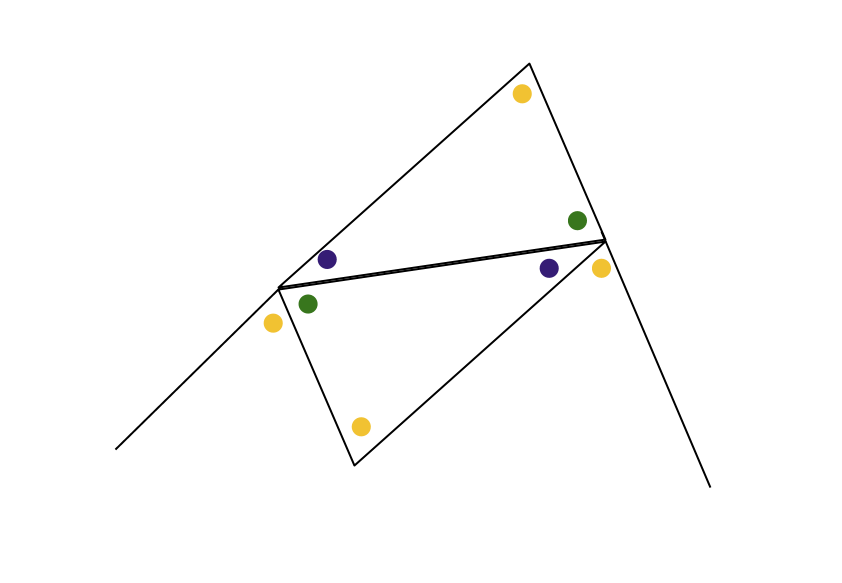
Jo, men det går bra! Dra undersidan genom den understa punkten på så vis att en blå vinkel bildas till vänster och en grön till höger. Var alla de oavslutade linjerna skär varandra finner vi triangelns två hörn och där kommer även vinklarna vara av rätt färg, eftersom vinkelsummorna i vänster- och högertrianglarna automatiskt kommer stämma. Och vi har redan bevisat att i den här konstruktionen kan inte alla fyra trianglarna vara kongruenta.
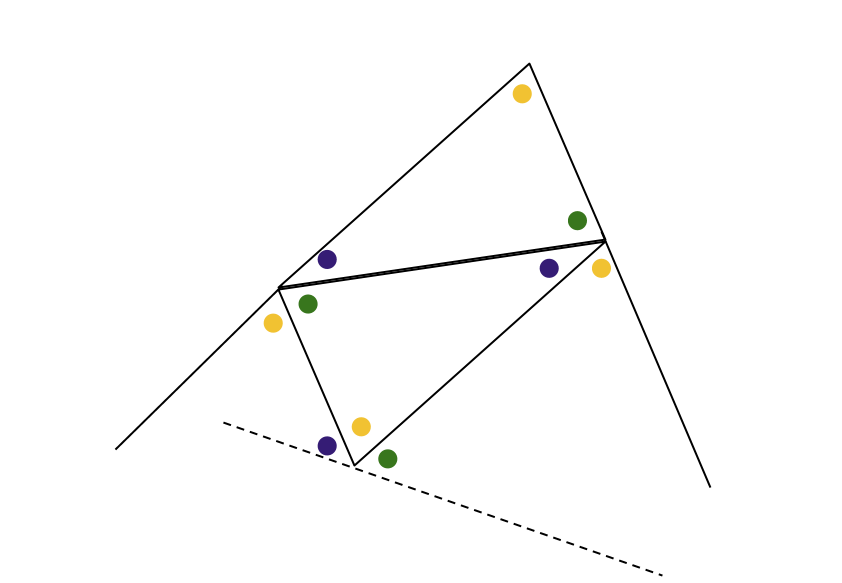
Vi är klara!
Fel
Men kan göra fantastiskt många fel här! Glömma olika fall, inte utnyttja att vinklarna måste vara olika i sin resonemang, anta att vinklarna måste vara olika så fort det är tre stycken som kompletterar varandra. Det är även väldigt lätt att glömma bort att motivera att ens konstruktion är möjlig i den andra delen av problemet.
