gyllene snittet – Mattebloggen

Phi-växter, pi-växter och e-växter, del 2

I del 1 kom vi fram till att en växt inte bör växa med en rationell vinkel. Det vill säga, om vinkeln bladen emellan är 360/(p/q), så kommer växter sabba solljuset för sig själv efter p blad.

Om p=5 och q=2 så växer bladen ut med 360/(5/2)= 144 graders mellanrum. Det innebär att nya blad sprutar ut 144, 288, 432 (det vill säga 72), 216 graders mellanrum i förhållande till det första. Men nästa blad, det sjätte, kommer hamna 360 grader ifrån det första, det vill säga på exakt samma ställe! Detta är väldigt ooptimalt för en växt.

Oavsett vad för rationellt tal vi tar kommer samma elände att hända efter p blad, eftersom då har bladen avlagt 360/(p/q)*p = q*360 grader, alltså ett helt antal varv. Växten vill att det aldrig riktigt ska bli helt.

Så händer det inte med de irrationella talen. Låt oss jämföra vad vi får för irrationella växter. I tabellen ser du en rationell växt, en phi-växt, en pi-växt och en e-växt. Början ser det relativt likt ut emellan alla växterna:

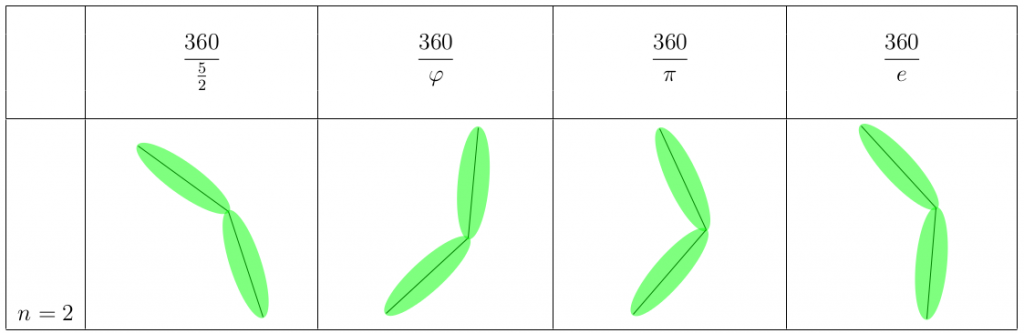
Men efter fem blad har den första växten fördelat sina blad jämnt, medan de andra ser annorlunda ut. Phi-växten har fördelat sina blad ganska bra, medan pi-växten har sina blad onödigt trångt.

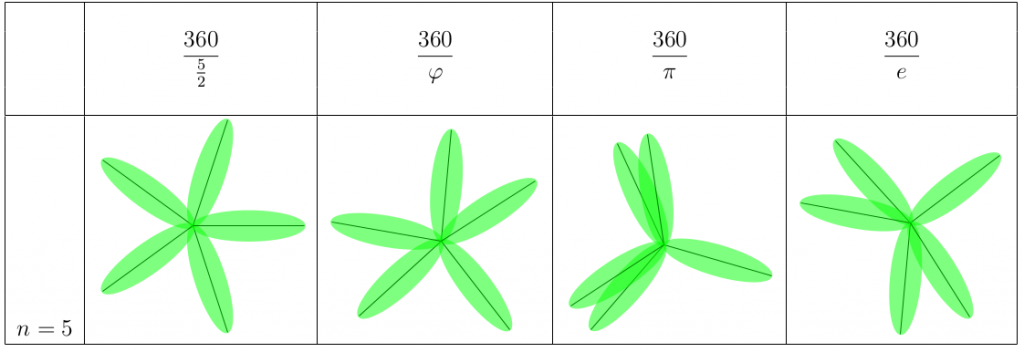
Vad händer vid 12 blad? Oförändrat för den rationella växten – den kan bara ha sina blad på 5 positioner. Phi-växten är jämnfördelad som vanligt, e-växten är också ganska bra. Pi-växten har däremot tre tydliga delar. Kan det ha att göra med att pi på ett ungefär är lika med 3?
n12

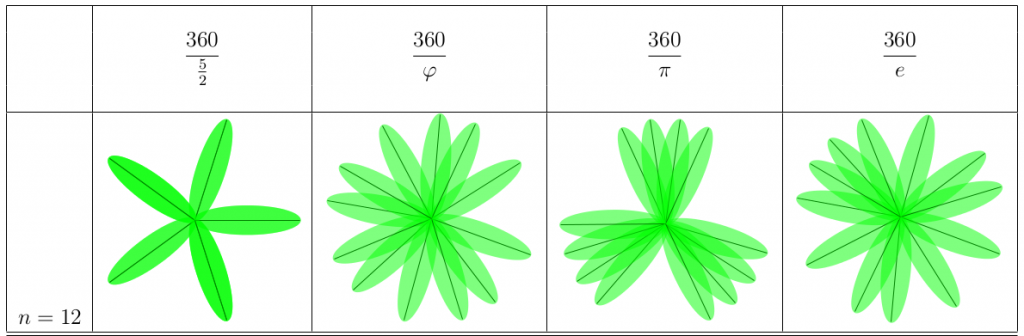
Vi 30 ser vi hur växterna klarar av många blad. De mörkare partierna visar på att bladen överlappar varandra, vilket sker mer och mer på e-växten och pi-växten speciellt. Överlappningen finns hos phi-växten också, men den är mer jämnfördelad. Notera att pi-växten har 22 tydliga delar!
n30

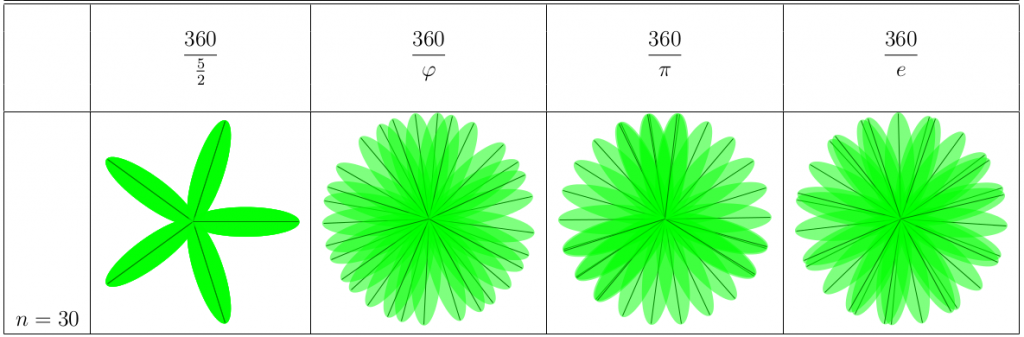
Till sist kollar vi riktigt många blad, 50. Pi-växten har 22 väldigt tydliga delar, e-växten har 19, medan phi-växten aldrig har två blad så pass nära varandra som de andra växterna. Den verkar ha 5 stora delar, vilket tyder på att vi i verkligheten skulle se 5 spiraler för den bladstorleken.
n50

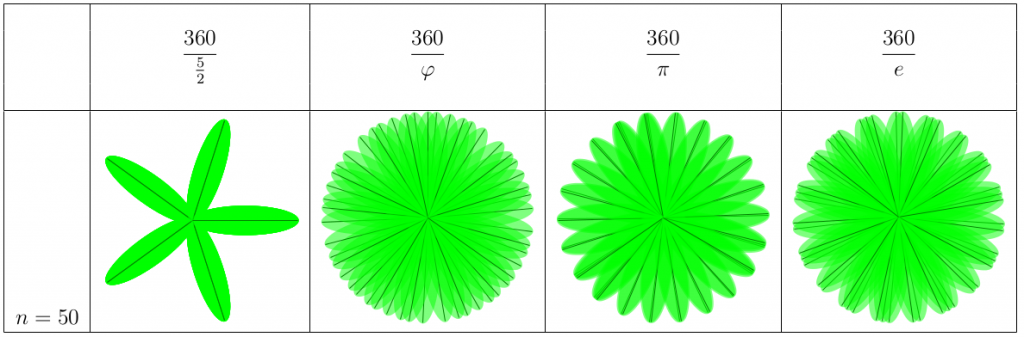
Varför blir det 22 tydliga delar hos pi-växten? Det har att göra med att pi approximeras väldigt bra med talet 22/7 (ca 3,14), vilket får växten att agera som en vanlig rationell växt och överlappa sina egna blad efter 22 stycken. Varför är vissa växter ändå pi-växter, som vi såg i förra delen? Jag gissar på att många verkliga plantor inte har så många blad eller grenar, och därför spelar det inte så stor roll för dem att det blir problem efter 22 stycken. De satsar snarare på 3 eller något sådant.

På samma sätt är 19/7 ett rationellt tal nära talet e (men inte lika när som 22/7 är pi), därför bildas det 19 delar på e-växter. Jag vet inte varför jag inte träffat på e-växter hittills, de verkar ju växa helt ok i början.

Men talet phi är väldigt speciellt. Det finns inte någon rationell approximation av det talet som är i någon mening så bra som 22/7 är för pi. Visst, vi kan använda större nämnare för att få ett rationellt bråk som är så nära phi som vi vill, men då blir nämnarna nästan onaturligt stora. För mer rigorös definition av bra rationella approximationer, se Hurwitz sats. Konstanten i satsen kommer just ifrån phi, det gyllene snittet, och det är det som medför att phi är det mest irrationella talet.

Det innebär att just den konstanten är optimal för växter med stort antal blad, frön, grenar etc. och det är därför vi vanligen finner just 34 och 55 spiraler på solrosor och inte 22 (Klicka på bilden för att räkna själv).

Phi-växter, pi-växter och e-växter, del 1

Hur kommer det sig att det finns spiraler på kottar, kronärtskockor och ananaser? Om du inte har sett förklaringen, rekommenderar jag Vi Harts videoserie ”Spirals, Fibonacci, and Being a Plant”: del 1, del 2 och del 3.

(Eller kolla upp en sida på svenska med många bra bilder.)

kotte

En av sakerna som avslöjs är att växternas blad växer ut med en och samma vinkel i förhållande till föregående bladet, nämligen vinkeln $\frac{360^\circ}{\varphi}$ , där $\varphi$ är det gyllenne snittet, även kallad det mest irationella talet. Detta för att bladen aldrig ska hamna direkt över och blockera solljus för varandra.

Eftersom bladen inte är hur tunna som helst, kommer de så småningom ändå överlappa varandra delvis. Därför bildas det spiraler, vilket förklaras i videorna. Men varför är antalet spiraler alltid lika med ett fibonaccital, för tallkottar oftast 5, 8 eller 13 (plocka upp en kotte och räkna spiralerna åt båda hållen)?

Min förklaring är att gyllene snittet approximeras med exempelvis 8/5, vilket betyder att växten efter 8 blad har avlagt $8\cdot\frac{360^\circ}{\varphi}$ grader, vilket är ungefär lika med $8\cdot\frac{360^\circ}{\frac{8}{5}}$ grader, det vill säga typ 5 varv. Och så med alla andra heltalsapproximationer, när växten
har gått ett ungefär helt antal varv, så har det vuxit ut ett fibonacciantal blad. När ett nytt varv börjar, bara då kan spiralerna börja växa, och därför är antalet spiral lika med antalet blad som vuxit ut hittills, det vill säga ett fibonaccital.

Vi sade förut att $\varphi$ var det mest irrationella talet. Vad ska det betyda? Alla irrationella tal är ju lika irrationella, men vissa tydligen mer irrationella än andra. För växten innebär det att det nya bladet dyker upp inte bara på en ledig plats, utan också på en plats där det finns som mest utrymme (jag vet inte riktigt hur detta ska förklaras matematiskt).

Men varför skulle inte en växt kunna växa med en annan irrationell vinkel, som exempelvis $\frac{360^\circ}{\pi}$ eller $\frac{360^\circ}{e}$ grader? Talet $\frac{22}{7}$ är ju en väldigt bra approximation av $\pi$ , så varför skulle inte en sådan $\pi$ -växt kunna ha 22 spiraler?

Nu när jag inte kan spekulera mer matematiskt, går jag ut i naturen och letar. De första två växter jag hittar verkar vara typiska $\varphi$ -växter, men den tredje har vinkeln närmare $114,6^\circ$ , det vill säga $\frac{360^\circ}{\pi}$ !

Eller nja, inte om man kollar på de färdigväxta bladen, då är det en vanlig $\varphi$ -växt:
SAMSUNG

Den här då? Det är lite svårt att se i vilken ordning bladen har växt ut.

SAMSUNG

Men om det är någon av våra förmodade vinklar, bladen emellan, så är det i alla fall $\pi$ :

SAMSUNG

Hurra! En $\pi$ -växt! Så inte alla växter följer $\varphi$ -lagen… Eller har jag mätt fel? Varför är de flesta växter ändå $\varphi$ -växter?

Kan du hitta andra irrationell växter i naturen, kanske med vinkeln $\frac{360^\circ}{\sqrt{2}}$ mellan bladen? Om en vecka kommer jag med mer spekulationer och förklaringar om växternas utväxtvinklar.

Fibonaccitalen och gyllene snittet

Ett välkänt trick är att man kan klippa en triangel i bitar, arrangera om bitarna, sätta ihop dem till en triangel igen och få en extra ruta!

Hur kan det stämma? Nedan kommer förklaringen, men fundera själv först!

.

.

.

.

.

.

.

.

De stora figurerna är egentligen inte trianglar, det ser bara ut som det. Vore de riktiga trianglar, skulle den gula och den röda triangeln vara likformiga, det vill säga ha samma förhållande på kateterna. Men $\frac{5}{2}\neq\frac{8}{3}$ (eftersom $\frac{3}{2}\neq\frac{8}{5}$ ).
Så att den första figuren är en inåtböjd ”triangel” och den andra är en utåtböjd. Därifrån kommer den extra rutan.

Låt oss jämföra liknande, men annorlunda bråk: $\frac{3}{2}$ och $\frac{8}{5}$ .
$\frac{3}{2}=1,5$

$\frac{8}{5}=1,6$
Ganska nära värden! Därför har även $\frac{5}{2}$ och $\frac{8}{3}$ ganska nära värden. Förhållanden mellan sidorna är så pass lika att trianglarna är nästan likformiga och har nästan likadana vinklar. Det innebär att deras hypotenusor bildar nästan en linje (och för oss ser det ut som att de bildar en linje).

Låt oss studera fler förhållanden:

$\frac{13}{8}=1,625$

$\frac{21}{13}=1,61538462\ldots$

$\frac{34}{21}=1,61904762\ldots$

$\frac{55}{34}=1,61764706\ldots$

$\frac{89}{55}=1,61818182\ldots$

Den noggranna läsaren kanske har upptäckt att de nya täljarna får man genom att addera de föregående två:

$21=13+8$

$34=21+13$

$55=34+21$

$89=55+34$

Och några känner igen Fibonaccitalen i nämnarna och täljarna:

$1,1,2,3,5,8,13,21,34,55,89\ldots$

Fibonaccitalen startar med 1 och 1, sedan får man nästa tal genom att lägga ihop de två föregående.

Låt oss se om bråken (som är lika med förhållanden mellan två Fibonacci-granntal)

$\frac{2}{1},\frac{3}{2},\frac{5}{3},\frac{8}{5},\frac{13}{8},\frac{21}{13},\frac{34}{21},\frac{55}{34},\frac{89}{55},\ldots$

i slutändan blir lika med något värde. Vi har ju sett på de tidigare att värdet verkar vara nära $1,6$ .

Man kan skriva om bråken till så kallade kedjebråk:

$\frac{2}{1}=1+\frac{1}{1}$

$\frac{3}{2}=1+\frac{2}{1}=1+\frac{1}{\frac{2}{1}}=1+\frac{1}{1+\frac{1}{1}}$

$\frac{5}{3}=1+\frac{2}{3}=1+\frac{1}{\frac{3}{2}}=1+\frac{1}{1+\frac{1}{1+\frac{1}{1}}}$

Varje bråk blir lika med 1+1/(föregående bråk) och därför ser alla de bråken ut på ett och samma sätt. Det är bara antalet ettor i kedjebråket som ökar för varje steg.

Låt oss anta att vi får något reellt tal $\varphi$ , om vi utför operationen oändligt många gånger:

$\varphi=1+\frac{1}{1+\frac{1}{1+\ldots}}$

Då måste

$1+\frac{1}{\varphi}=1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\ldots}}}=\varphi$

$\varphi=1+\frac{1}{\varphi} \iff \varphi^2-\varphi-1=0$

Ekvationen har exakt en positiv lösning:

$\varphi=\frac{1+\sqrt{5}}{2}\approx 1,61803399$

Detta tal kallas gyllene snittet och är lika med vissa proportioner i Da Vincis målning ”Den vitruvianske mannen”. Många andra saker i naturen har den proportionen också, just på grund av att mycket i naturen beter sig som Fibonaccital (se början på videon):

Om du tyckte om Fibonaccitalen försök att lösa följande två problem:

1. Klipp upp en kvadrat med sida 1 i tre eller fyra delar och sätt ihop delarna till en rektangel med sidorna $\varphi$ och $\varphi-1$ .

2. Klipp upp en kvadrat med sida 8 i tre eller fyra delar och sätt ihop delarna till en nästan rektangel med sidorna 5 och 13. (Du kan öka Fibonaccitalen i problemet och se ”felet försvinna”.)

(Bonusproblem. Bråken
$\frac{5}{2},\frac{8}{3},\frac{13}{5},\frac{21}{8},\frac{34}{13},\ldots$
närmar sig ett värde. Vilket?)

Jag tackar Djalal för tipset om ovanstående problem och diskussion.