Valentina Chapovalova

Mattecirkelns första träff

Första träffen på höstens mattecirkel äger rum på onsdagen den 2:a september kl. 15.20 i sal 169 på Katedralskolan i Uppsala. Alla nyfikna är välkomna! Det enda man behöver ha med sig är penna och papper.

Karta

Klassiska bevis: Cevas sats, del 2

Detta inlägg är fortsättning på del 1 om Cevas sats. Första delen förklarar satsens formulering och ger tips för hur man skulle kunna bevisa den. Den här delen innehåller själva beviset.

Cevas sats

Given är en triangel ABC. Tre cevianer AM, BL och CK skär varandra i samma punkt om och endast om $\frac{AL}{LC}\cdot\frac{CM}{MB}\cdot\frac{BK}{KA}=1$

Bevis:

Antag först att cevianerna skär varandra i en och samma punkt O. Vi skall visa att värdet av uttrycket verkligen är 1.

Notera till exempel att trianglarna COM och MOB har lika stora höjder utgående från punkten O, eftersom deras baser ligger på samma linje. Låt höjderna ha längden h. Därför kan vi enkelt uttrycka förhållandet mellan dessa två areor:

$\frac{S_{COM}}{S_{MOB}}=\frac{\frac{CM\cdot h}{2}}{\frac{MB\cdot h}{2}} = \frac{CM}{MB}$

Eftersom trianglarna CAM och MAB också har lika långa höjder, utgående från A, så kommer deras areor också att förhålla sig som $\frac{CM}{MB}.$

Låt $\frac{CM}{MB} =$ k (något reellt tal). Men om $S_{CAM}$ är k gånger större än $S_{MAB}$ och $S_{COM}$ är k gånger större än $S_{MOB}$ , så är differensen, $S_{COA}$ , också k gånger större än $S_{AOB}$

Det vill säga $\frac{S_{COA}}{S_{AOB}}=\frac{CM}{MB}$

Med analogiska resonemang får vi förhållanden mellan de andra par av de färgade trianglarna:

$\frac{S_{AOB}}{S_{BOC}}=\frac{AL}{LC}$
$\frac{S_{BOC}}{S_{COA}}=\frac{BK}{KA}$

Därför kan vi skriva om uttrycket:

$\frac{AL}{LC}\cdot\frac{CM}{MB}\cdot\frac{BK}{KA}=\frac{S_{AO B}}{S_{BOC}}\cdot\frac{S_{COA}}{S_{AOB}}\cdot\frac{S_{BOC}}{S_{COA }}=1$

eftersom allt förkortas i det omskrivna uttrycket.

Nu har vi kvar att bevisa att värdet på uttrycket inte kan vara 1 utan att cevianerna skär varandra. Vi antar motsatsen, det vill säga att värdet är 1, men cevianerna råkade inte skära varandra i samma punkt:

trefulacevianer Nu är vi så smarta som möjligt och använder oss av del 1, som vi redan har bevisat. Precis som i följande berättelse:

En matematiker och en fysiker löser praktiska uppgifter. De blev tillsagda att koka upp 1 liter vatten med hjälp av en vattenkran och en vattenkokare. Båda fyller förstås sin vattenkokare med vatten och sätter på den.

Nästa uppgift är annorlunda: de får en vattenkokare full med vatten och ska nu igen koka upp 1 liter vatten.

Vad gör en fysiker? Han ställer vattenkokaren på plattan och sätter på den förstås.

Vad gör en matematiker? Han häller ut vattnet och därmed ska han lösa praktisk uppgift nummer ett, vilket han redan kan.

I detta fall är det förstås inga onödigheter vi sysslar med. Men på samma sätt som i berättelsen ska vi göra någonting, för att kunna använda oss av tidigare kunskaper. Vi drar en ny linje, för att få samma situation som förut. Dra linjen CK’, som går igenom skärningspunkten för cevianerna AM och BL.

fyracevianer

Från del 1 vet vi att följande måste gälla:

$\frac{AL}{LC}\cdot\frac{CM}{MB}\cdot\frac{BK'}{K'A}=1$

Men enligt antagandet har vi också

$\frac{AL}{LC}\cdot\frac{CM}{MB}\cdot\frac{BK}{KA}=1$

Bland annat är uttrycken lika med varandra och på så sätt får vi $\frac{BK'}{K'A}=\frac{BK}{KA}$ , vilket i sin tur implicerar att $BK'\cdot KA=K'A\cdot BK$ , vilket är omöjligt, eftersom BK<BK’ och K’A<KA. Motsägelse, alltså var situationen omöjlig!

Således så fort uttrycket är lika med 1, så måste cevianerna skära varandra i en punkt.

Användningar för satsen

På så sätt har vi i princip bevisat flera satser på en gång, till exempel att medianerna i en triangel skär varandra i en och samma punkt. Samma sak gäller för bisektriserna, samma för linjer som förbinder hörn och tangeringspunkter för den inskrivna cirkeln. Det lämnas åt läsaren att komma på hur man ska använda Cevas sats för att visa de egenskaperna.

Klassiska bevis: Cevas sats, del 1

Cevas sats är ett av de vackraste geometriska faktum för trianglar. Men för att kunna formulera satsen lättare, ska vi först definiera vad en cevian är för något.

Cevianer

Medianen är ju en ganska känd sträcka, det är den som går ut från ett hörn på en triangel och slutar på motstående sidan på så sätt, att den delas mitt itu. Notera att en triangel har tre olika medianer.

Bisektrisen är också en kändis. Den är den sträckan i triangeln som delar vinkel mitt itu. Även bisektriserna är tre i en triangel.

Även om vi drar en sträcka från hörn till sida, som inte alls är speciell, så vill vi kalla det för något. Vi säger att det är en cevian. Cevianer är alltså ett samlingsnamn för medianer, bisektriser, höjder osv. Notera att mittpunktsnormaler inte är cevianer.

Cevas sats

Given är en triangel ABC. Tre cevianer AM, BL och CK skär varandra i samma punkt om och endast om $\frac{AL}{LC}\cdot\frac{CM}{MB}\cdot\frac{BK}{KA}=1$

”Om och endast om”:

Detta är en väldigt vanlig förkortning i matematiken. Istället för att skriva att man ska bevisa två saker (”om” och ”endast om”), sätter man ihop dem i en och samma mening. I detta fall är de två sakerna man ska visa:

1. Om AM, BL och CK skär varandra i samma punkt , så gäller $\frac{AL}{LC}\cdot\frac{CM}{MB}\cdot\frac{BK}{KA}=1$

2. Om $\frac{AL}{LC}\cdot\frac{CM}{MB}\cdot\frac{BK}{KA}=1$ , så skär cevianerna AM, BL och CK varandra i samma punkt.

Tankegång:

Som vanligt finns det många sätt att bevisa satsen. Ett av de mest kända använder areabegreppet. Det enda vi behöver är areaformeln för en triangel: arean är lika med basen gånger höjden delat på två. Vi betecknar i fortsättningen arean av triangeln ABC med $S_{ABC}$ .

areanaventriangel

För att använda detta i vårt problem gäller att komma på att beteckna (den eventuella) skärningspunkten med O och dela upp triangeln i tre mindre: AOB, BOC och AOC.

cevaareor

Det är förstås omöjligt att veta de exakta areorna hos de olikafärgade trianglarna. Men vi kan uttrycka hur areorna förhåller sig med hjälp av sträckorna, som förekommer i uttrycket.

Nu finns det nog med tips för att bevisa satsen på egen hand. Försök själv eller vänta på nästa inlägg!

Mattecirkel på Katedralskolan i höst

Jag är glad att annonsera nyheten: det kommer hållas en matematikcirkel för intresserade gymnasieelever i höst! Som bas kommer jag att ha Katedralskolan i Uppsala (alternativt rektorsvillan), men elever från alla skolor är givetvis välkomna.

Detta har jag sett fram emot länge. Det som börjar i höst är dock på lite högre nivå än högstadiet och kanske med mer vikt på tävlingsproblem. Mattecirkeln ska kunna förbereda eleverna för Skolornas Matematiktävling, SMT.

Cirkeln välkomnar eleverna i årskurs 1-3 och även nyfikna 9:or. Man behöver inga förkunskaper än högstadiematte och cirkeln kommer inte att ta upp så mycket av skolmaterialet (Matte A, B osv). Uppgifterna som kommer att tas upp liknar snarare gåtorna på den här bloggen.

Vi drar i gång ungefär i mitten av september! Jag återkommer med mer information.

Mattekollo

Ännu en juli har passerat då jag har jobbat som lärare på ett mattekollo. Det var en spännande månad med tonvis jobb och upplevelser.

Vi organiserade lekar och sportaktiviteter, film- och spelkvällar, men framförallt var vårt uppdrag att utbilda tonåringar i matematik. Kollot har ett intagningsprov, ett arbete man måste skicka in för att visa att man är välförberedd vad det gäller matematiska kunskaper och färdigheter. Och även många av dem som kommit in har det ganska svårt på lektionerna.

Detta skedde då i Ryssland, man kan se att systemet skiljer sig från den svenska då ”alla som vill ska med”. Man kan undra om det finns någon poäng med denna elitism bland barn, vad är egentligen vitsen med att hårdträna dem så tidigt?

Jag skulle vilja påstå att det inte spelar så stor roll att de lär sig just matte. Ämnet är tyvärr oftast föräldrarnas val. Det viktigaste för mig på kollot är att uppfostra tänkande individer. Att sammanföra på detta sätt skola, lek och vänner ger dem en positiv upplevelse av utbildning, hur svår den än må vara.

Eftersom alla har föräldrarna långt borta är alla i samma situation. De vuxna de får umgås med är oftast intressanta engagerade människor (vi ;) ). Om ett barn verkligen är blivande matematiker, kan hon/han välja och vraka bland förebilder.

Det jag inte tycket om är att barnen kan bli för resultatinriktade. De tar med sig betyghetsen från vanliga skolor och blir ledsna ifall inte allting går perfekt. För om man inte får godkänt, kommer man antagligen inte få åka på kollot året därpå. Vilket så gott som alla våra barn ville!

Sommaruppehåll

semester Äntligen har sommaren intagit Sverige och för de flesta av oss innebär detta upphåll från matten.

Inte dock för de som läser sommarkurser och faktiskt inte för mig heller! Min semester spenderar jag på ett mattekollo i Ryssland.

Det innebär för min del att spendera en månad ute i ingenstans i en skog tillsammans med några vuxna och några hundra barn som vi ska lära någon sorts matte. Och samtidigt ansvara för att de mår bra och har skoj. Justja, några miljoner myggor kommer finnas där också.

Förhoppningsvis kommer jag uppdatera lösningarna på de senaste mattegåtorna. Det går fortfarande bra att skicka in lösningsförslag på de sista två. Efter det är den inoficiella tävlingen slut för terminen.

Redan nu kan man konstatera att Johan har vunnit tävlingen och det är kanske inte så konstigt, ty han är doktorand!

Bloggen återkommer till liv den 1 augusti och tills dess, ha en kanonsommar!

Dyra uträkningar

Rekommenderad från: 12 år

[kkratings]

Använd valutan euro, mynt och sedlar, för att beteckna talen 1, 2, 5 och 10. Med hjälp av dem och (gratis) parenteser och de fyra räknetecken (+, -, *, /) bilda ett uttryck, vars värde är 2009, genom att spendera så lite pengar som möjligt.

v26

Visa lösningen

Diskussion:

Notera att man aldrig ska använda 10:or i sitt uttryck, eftersom de kan ersättas med 2*5. På så sätt använder vi 7 euro i stället för 10 euro.

Ett snabbt sätt att komma upp i höga tal är att använda multiplikation. Vi försöker till exempel att faktorisera talet 2009 och skriva faktorer med hjälp av 1:or, 2:or och 5:or.

2009=41*49=41*7*7=(2*2*2*5+1)*(2+5)*(2+5)

Här använder vi 2+2+2+5+1+2+5+2+5=26 euro, vilket man skulle kunna tro är svaret. Men i uttrycket ovan förekommer faktorn 7, som är ”dyr”. Talet 8 skulle vara ”billigare”, bara kosta 6 euro (2*2*2=8). Vad händer om vi istället försöker faktorisera 2008 eller 2007?

Ett svar:

Genom att prova med olika tal kommer man fram till att det går att klara sig med 25 euro:

2009=2008+1=2*2*2*251+1=2*2*2*(5*5*5*2+1)+1

(2+2+2+5+5+5+2+1+1=25).

Jag har dock inget bevis för att det är det minsta möjliga antalet pengar man behöver använda.

Uppdatering:

Johan kom på ett sätt, där det går att klara sig med 24 euro. Tricket är att se 7:or som 2*(2+1)+1, det vill säga att de kostar bara 6 euro.

2009 = 49*41 = 7*7*41 = (2*(2+1)+1)*(2*(2+1)+1)*41 = (2*(2+1)+1)*(2*(2+1)+1)*(2*2*2*5+1)

2+2+1+1+2+2+1+1+2+2+2+5+1=24

Men det finns fortfarande inget bevis för att det skulle vara det minsta antalet pengar. Vi måste på något sätt bevisa att det aldrig går med 23 (eller hitta på ett exempel då det går).

Allmänna saker man kan säga är att multiplikation är det bästa sättet att få fram stora tal. Då är frågan vilka tal som är bäst att multiplicera, för att vi ska få så stort resultat som möjligt och spendera så lite pengar som möjligt. Vi struntar just nu i att uppgiften handlar om talet 2009.

1 är meningslöst att multiplicera med sig självt.

2-potenser är 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048 och så vidare. De kostar 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22 euro respektive.

3-potenser är 3, 9, 27, 81, 243, 729, 2187 och så vidare. De kostar 3, 6, 9, 12, 15, 18, 21 euro respektive.

4-potenser kostar lika mycket som 2-potenser, eftersom 4=2*2.

5-potenser är 5, 25, 125, 625, 3125 och så vidare. De kostar 5, 10, 15, 20, 25 euro respektive.

Här ser vi att 3-potenser egentligen är bäst bland de här, eftersom för 21 euro kan vi få 2187, medan ett mindre tal 2048 kräver för 2-potenser hela 22 euro. På liknande sätt kan vi jämföra med 5-potenser: 625 kostar 20 euro, men med 3-potenser kan vi få talet 729 med bara 18 euro.

Men vad händer om vi fortsätter med 6, 7, 8 euro? Där finns det bättre sätt att skriva just de talen än 1+1+…+1, nämligen

6 = 2*(2+1) fås med 5 euro,

7 = 2*(2+1)+1 fås med 6 euro (som förut),

8 = 2*2*2 fås med 6 euro (och i så fall blir lika bra som 2-potenser).

Vi kan se att i omskrivningar av de här talen använde vi faktiskt endast multiplikation med 2 och 3 och plussade på 1:or när det behövdes. Det tyder på att multiplikation med 2-3 är optimal. Det har att göra med att talet e = 2,718281828… ger snabbast tillväxt vid multiplikation med sig själv, men vi kan ju bara använda heltal.

Detta var egentligen Johans funderingar också, men vi har fortfarande inte kommit på något sätt att lösa gåtan helt. Alla ytterligare förslag är välkomna!

Ännu en uppdatering:

2009 = (2*3+1)*(2*4*4*3*3-1)
och talen 3 och 4 skrivs som 4=1+1+1+1, 3=1+1+1.

En följd av fyrhörningar

Rekommenderad från: 15 år

[kkratings]

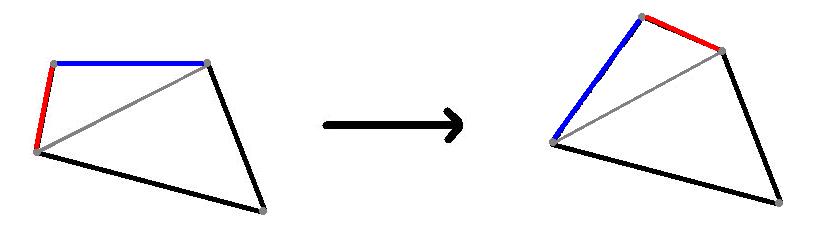
Låt F₁ vara en godtycklig konvex fyrhörning. För k>1, F_k konstrueras genom att man skär F_k-1 i två delar längs en av dess diagonaler, vänder på en av delarna och sedan klistrar delarna samman längs samma diagonal. Bestäm det största möjliga antalet icke-kongruenta fyrhörningar i följden {F_k}.

Exempel:

För att förtydliga, en tillåten operation är följande:

lv25_1

Visa lösningen

Notera att om sidlängderna hos fyrhörningen är a, b, c, d, så finns exempel, där följden av fyrhörningar innehåller 6 icke-kongruenta: de med olika ordning på sidorna. Tag nämligenen fyrhörning med alla sidor olika, men som ändå påminner om en kvadrat (detta för att fyrhörningarna som bildas inte ska bli icke-konvexa). Men tillåtna operationer byt sedan plats på sidorna på alla möjliga sätt (trianglar med den gråa symbolen flippas):

l25

Ritningen är inte exakt, men vi kan se att alla olika sidordningar verkligen förekommer. Eftersom fyrhörningar kan roteras, valde vi fixera sidan med längden a, den kommer ändå alltid finnas.

Så nu är frågan varför det inte går att konstruera fler fyrhörningar? Notera att det finns en sak som aldrig förändras och det är summan av två motsatta vinklar i fyrhörningen. Vid varje flipp är det ett par av motsatta vinklar som inte ändras, således kommer vinkelsumman i det andra paret inte heller förändras.

Men notera också att sidlängderna kvarstår. Tag nu någon ordning på sidorna, vi skall nu bevisa att det går att bygga exakt en fyrhörning med den ordningen ur den ursprungliga. Utan inskränkning kan vi anta att sidordning är (medurs) a, b, c, d och a är den vänstra sidan.

Kalla vinkeln mellan a och d för x. Då är vinkeln mellan b och c också bestämd, nämligen S-x, där S var vinkelsumman av den ”nedre vänstra” och den ”övre högra” vinkeln. Men då har vi två trianglar, beståndsdelarna i fyrhörningen, som kan sättas ihop endast på ett sätt och det endast när de okända sidorna är lika (de ska bli en diagonal).

l25_2

De okända sidorna är lika endast för en vinkel x (den som det går att konstruera bilden för). Det beror på att om vinkeln minskas, så minskas också den motstående sidan. Men då ökar S-x och dess motstående sida, och då kan de sidorna inte längre vara lika. Samma sak händer om vinkeln x ökas.

På så sätt har vi uttömt alla fallen och visat att antalet olika fyrhörningar är 6, en för varje sidordning.

Ljug när du föreläser

Bra fysikföreläsare på Uppsala universitet lyser med sin frånvaro, men nyligen hörde jag talas om ett undantag. Jag vet inte vem det är och kommer inte ihåg varför han var bra, men ett undervisningsknep tänker jag någon gång låna från honom.

Innan varje föreläsning försäkrar han om att någon gång under föreläsningen kommer han att ljuga. Det kan vara allt från ett litet faktafel och felräkning på tavlan till dåligt resonemang gällande någon komplicerad förklaring. Poängen är att studenterna då skall reagera och säga åt läraren eller ställa en fråga om det som känns felaktigt.

Tänk er en morgontidning den 1:a april. De flesta stora tidningarna har garanterat någon skämtartikel den dagen och det gäller att komma på vilken. Men det är inte så lätt att komma på!

Jag brukar snabbt bli misstänksam över någon nyhet och tänker ”näää, det där kunde väl aldrig ha hänt”, men sedan vänder jag sidan och har en exakt samma tanke för nästa nyhet. Nästa dag visar det sig att båda nyheterna var riktiga och det var en helt annan grej som var på skämt. Detta visar på att min förmåga att kritisk tänka över nyheter är näst intill obefintlig.

Men samma princip om kritiskt tänkande kan tillämpas på matematiken. Om man inte riktigt kan skilja på sanning och lögn under en föreläsning så accepterar man istället allting godtroget. Även om läraren gör något uppenbart räknefel är det många som inte vågar påpeka det. De litar inte på sin förmåga att urskilja matematiskt sanning från lögn och det kan bero på flera saker. Kanske tränar man inte förmågan särskilt ofta eller så kan man inte tillräckligt om ämnet, som i fallet med mig och nyheter.

”Ljuga på varje föreläsning”-strategin skulle passa utmärkt på matematikföreläsningar. Frågan är ifall den lämpar sig bäst för ”äldre” studenter, som har fått lite kött på benen när det gäller matte, men jag anser inte det. På samma sätt som att man lär ett barn att simma genom att kasta det i vattnet så lär man nya studenter att orientera sig i matte genom att tvinga dem till att göra det.

Den här strategin får elever att lyssna nogrannt, ställa frågor så fort det finns någonting oklart och hindrar dem från att fastna i ett transliknande tillstånd ”skriv av allt från tavlan” (för något kan ju vara fel och då får man skriva om). Varje föreläsning får de en ny intellektuell utmaning, varje gång kommer de ”läsa tidningen” lika noggrant som 1 april!

Så du som har undervisning, prova att ljuga för dina studenter (berätta om det först för dem såklart) och skriv hur det gick!

Turistens promenad

Rekommenderad från: 12 år

[kkratings]

En turist vill ta en promenad i Gamla Stan från busshållplatsen (punkt A) till sitt hotell (punkt B). Han vill ha en så lång rutt som möjligt. Han tycker att det är tråkigt att komma tillbaka till korsningar där han har varit förut, så det undviker han. Rita en så lång rutt som möjligt åt turisten och visa att det inte finns längre.

v24

Visa lösningen