Mattebloggen

Matteproblem vecka 20

På ett lager fanns likadana ostar. En natt kom sluga råttor dit och åt upp 10 av ostarna. Varje råtta åt lika mycket. Några råttor klarade dock inte av måltiden och fick ont i magen. Nästa natt kom de 7 råttorna som inte fick ont i magen och åt upp resten av osten. Dock fick varje råtta hälften så mycket som natten innan. Hur många ostar fanns det från början?

Matteproblem vecka 19

En fotboll är hopsydd av 32 lappar: vita sexkanter och svarta femkanter. Varje svart lapp gränsar till bara vita, varje vit lapp gränsar till tre vita och tre svarta lappar. Hur många vita lappar finns det i en fotboll?

Lösning till problem vecka 18

På bordet ligger en papperscirkel med radien 5 cm. Så länge det är möjligt, lägger Ilian till papperskvadrater med sidan 5 cm intill cirkeln så att följande villkor uppfylls:
1. Varje kvadrat har ett hörn som nuddar cirkeln.
2. Kvadraterna överlappar inte varandra.
3. Varje ny kvadrat nuddar den föregåendes hörn med ett hörn.

Bestäm hur många kvadrater Ilian kan lägga ut och visa, att den första och den sista kvadraten måste också nudda varandras hörn.

Jag fick in ett par fina lösningar, och jag kommer att använda mig av Erik T.’s bilder i lösningen (som ni kanske har märkt, ritar jag vanligtvis i paint, fastän jag borde ha lärt mig att TeX:a bilder för länge sen).

Lösning:

Säg att Ilian bestämmer sig för att lägga den andra kvadraten moturs från den första (det är symmetriskt ifall han lägger åt andra hållet). Det går bara att göra på ett sätt för att den nya kvadratens sida ska nudda både cirkeln och ett gammalt hörn (finns bara en punkt på cirkeln på avståndet 5 cm, som inte redan är upptagen).

Lägg på en till kvadrat, spelar inte så stor åt vilket håll, i vilket fall får vi tre kvadrater:

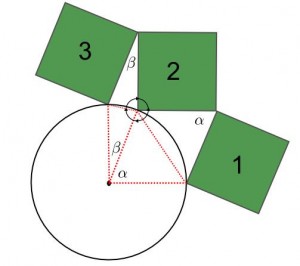
Eftersom cirkelns radie är lika med kvadraternas sidor, bildas figurer som kallas romber. En romb är en fyrkant med alla sidor lika. Man kan dela upp en romb i två trianglar och visa att trianglarna är kongruenta (sida-sida-sida). Då följer att rombens motstående vinklar är lika.

Den inringade vinkeln är 360°. Den består av en 90°-vinkel från kvadraten, samt två vinklar från var sin romb. Vinklarna från romberna är 180°-α respektive 180°-β stora. För att dessa tillsammans ska bilda en vinkel på 360°, måste α+β=90°.

Detta innebär att för varje två nya kvadrater bildas en ny 90°-vinkel runt cirkelns mittpunkt. Det finns tydligen plats för 8 kvadrater, eftersom hela vinkeln runt cirkelns mittpunkt är 360°.

α och β kommer dessutom alterneras (alla två romber bredvid varandra kommer att ge den sammanlagda vinkeln 90° runt cirkelns mittpunkt.

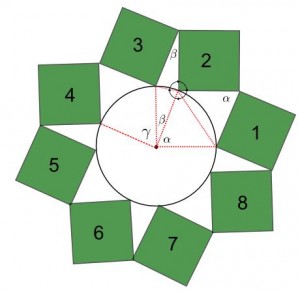
Således, om vi fortsätter att bygga på kvadrater kommer den nionde romben att sammanfalla med den första. Detta implicerar att den nionde kvadraten sammanfaller med den första. Alltså måste den åttonde och den första kvadraten nudda med hörnen (den åttonde och nionde gör det ju enligt konstruktionsreglerna). Så här ser det ut:

Lösning till problem vecka 17

En och samma fredagsfilm startade samtidigt på två televisionskanaler. Ena kanalen delade upp filmen i stycken om 20 minuter och sände 2 minuter långa reklampauser mellan filmstycken. Den andra kanalen delade upp filmen i 10 minuters-stycken och hade reklampauser som var 1 minut långa istället. På vilken kanal slutade filmen först?

Lösning:

Om en film delas upp i stycken, är antalet reklampauser 1 mindre än antalet stycken.

Så om filmen delas upp i x stycken om 20 minuter, kommer den att ha x-1 reklampauser. Och om varje reklampaus är 2 minuter lång, blir det 2x-2 minuter reklam.

Om samma film delas upp i stycken om 10 minuter, blir det dubbelt så många stycken, det vill säga 2x. Det innebär 2x-1 stycken reklampauser och om varje paus är 1 minut lång ger det 2x-1 minuter reklam.

Det är lika mycket tid själva filmen tar på båda kanalerna och i det första fallet är det mindre reklam. Så filmen slutar först på första kanalen!

Inför IMO 2010

imo Härmed vill jag gratulera min mattecirkelelev, Benjamin Fayyazuddin-Ljungberg, för att han har blivit utvald till det svenska laget i tävlingsmatematik!

Tillsammans med 5 andra gymnasister kommer han att representera Sverige i den 51:a Internationella Matematikolympiaden (IMO) i Kazakhstan. IMO är en årlig tävling för hela världens ungdomar och går ut på att eleverna ska lösa 6 problem under två tävlingsdagar. Det är då rätt så svåra problem, här kan ni se förra årets.

Det är riktigt roligt att ännu en av mina elever har blivit utvald till en av de 6 bästa i Sverige. Jag önskar honom lycka till på tävlingen (och jag kommer träna honom inför den så mycket som möjligt)!

Transformationsmatrisen – del 4

Vi vill göra livet så enkelt som möjligt för oss. Så vi räknar ut transformationsmatrisen som på det andra sättet i Transformationsmatrisen – del 3.

Vi kollar först på ett lite större exempel. Låt oss räkna ut transformationsmatrisen mellan baserna $A$ och $B$ , båda i 5 dimensioner. Säg att vi av någon anledning vet vad vektorerna $A_1, A_2, A_3, A_4$ och $A_5$ har för koordinater i basen $B$ :

$A_1=\left(\begin{array}{c}1 \\2 \\3 \\4 \\5\end{array} \right)_B$

$A_2=\left(\begin{array}{c}-1 \\-1 \\-1 \\-1 \\-1\end{array} \right)_B$

$A_3=\left(\begin{array}{c}0 \\0 \\0 \\0 \\1\end{array} \right)_B$

$A_4=\left(\begin{array}{c}1/2 \\1/2 \\0 \\0 \\0\end{array} \right)_B$

$A_5=\left(\begin{array}{c}5 \\2 \\2 \\2 \\5\end{array} \right)_B$

Och förstås vet vi dem i basen $A$ :

$A_1=\left(\begin{array}{c}1 \\0 \\0 \\0 \\0\end{array} \right)_A$

$A_2=\left(\begin{array}{c}0 \\1 \\0 \\0 \\0\end{array} \right)_A$

$A_3=\left(\begin{array}{c}0 \\0 \\1 \\0 \\0\end{array} \right)_A$

$A_4=\left(\begin{array}{c}0 \\0 \\0 \\1 \\0\end{array} \right)_A$

$A_5=\left(\begin{array}{c}0 \\0 \\0 \\0 \\1\end{array} \right)_A$

Vi betecknar transformationsmatrisen från bas $A$ till bas $B$ med $T$ så länge. Som vanligt får vi uppställningen:

$T\left(\begin{array}{c}1 \\0 \\0 \\0 \\0\end{array} \right)=\left(\begin{array}{c}1 \\2 \\3 \\4 \\5\end{array} \right)$

$T\left(\begin{array}{c}0 \\1 \\0 \\0 \\0\end{array} \right)=\left(\begin{array}{c}-1 \\-1 \\-1 \\-1 \\-1\end{array} \right)$

$T\left(\begin{array}{c}0 \\0 \\1 \\0 \\0\end{array} \right)=\left(\begin{array}{c}0 \\0 \\0 \\0 \\1\end{array} \right)$

$T\left(\begin{array}{c}0 \\0 \\0 \\1 \\0\end{array} \right)=\left(\begin{array}{c}1/2 \\1/2 \\0 \\0 \\0\end{array} \right)$

$T\left(\begin{array}{c}0 \\0 \\0 \\0 \\1\end{array} \right)=\left(\begin{array}{c}5 \\2 \\2 \\2 \\5\end{array} \right)$

T är en 5×5-matris. Om vi tittar noga på första multiplikationen $T\left(\begin{array}{c}1 \\0 \\0 \\0 \\0\end{array} \right)=\left(\begin{array}{c}1 \\2 \\3 \\4 \\5\end{array} \right)$ ser vi att det är nödvändigt att matrisen har $\left(\begin{array}{c}1 \\2 \\3 \\4 \\5\end{array} \right)$ som första kolonn.

På samma sätt följer de andra kolonnerna från de senare ekvationerna.

Alltså:
$T=\left(\begin{array}{ccccc}1 & -1 & 0 & 1/2 & 5 \\2 & -1 & 0 & 1/2 & 2\\3 & -1 & 0 & 0 & 2\\4 & -1 & 0 & 0 & 2\\5 & -1 & 1 & 0 & 5\end{array} \right)$

Eller, om vi kastar en blick tillbaka, så inser vi att de specifika siffrorna inte spelar någon större roll:
$T=\left(\begin{array}{ccccc}[A_1]_B & [A_2]_B & [A_3]_B & [A_4]_B & [A_5]_B\\\end{array} \right)$

med vilket menas att kolonnerna i matrisen är alla de vektorerna $A_1, A_2, A_3, A_4$ och $A_5$ uttryckta i basen $B$ .

Och det är precis vad vi behöver i det generella fallet.

För att bestämma transformationsmatrisen från bas $A$ till bas $B$ , uttryck basvektorerna i basen $B$ och skriv in resultaten som kolonner i en matris.

Riktigt så enkelt är det ju inte, den informationen som krävs har vi inte alltid från början. För att få veta hur man gör i ett jättegenerellt fall, kolla på nästa del.

Matteproblem vecka 18

Bestäm hur många kvadrater Ilian kan lägga ut och visa, att den första och den sista kvadraten måste också nudda varandras hörn.

Lösning till problem vecka 16

Thomas skrev ner alla dagar i en viss månad på en rad: 123456789101112… Sedan målade han över 3 av dagarna (som var hans kompisars födelsedagar) och inga övermålade dagar var precis efter varandra. Det visade sig att alla omålade områden består av exakt lika många siffror. Kan den första dagen vara oövermålad eller måste den vara övermålad?

För andra gången på kort tid använder jag mig av Erik R.’s lösning :)

Lösning:

Antag att den första dagen är omålad.

Det finns ett ojämnt antal ensiffriga dagar. Det innebär att om den första övermålade dagen är en tvåsiffrig dag, så måste det omålade området vänster om den ha ett ojämnt antal siffror.

Men det går inte, därför då måste även de andra omålade områdena, som består av tvåsiffriga tal, ha ett ojämnt antal siffror. Således måste den första övermålade dagen vara ensiffrig.

Men om den första övermålade dagen är ensiffrig, så har det omålade området vänster om den maximalt 8 siffror. Eftersom tre målade dagar som mest kan dela in sifferraden i fyra omålade områden kan det totala antalet siffror då max vara 8*4+1+2+2=37.

Men den kortaste månaden (februari i ett vanligt år) ger 9*1+19*2=47 siffror. Därmed kan ingen månad täckas in på detta vis.

Den första dagen måste därmed vara övermålad.

Matteproblem vecka 17

Lösning till problem vecka 15

På ett 10×10-bräde finns en pjäs i varje ruta. En tillåten operation är att välja en diagonal som innehåller ett jämnt antal pjäser och ta bort en valfri pjäs från den diagonalen. Hur många pjäser kan man som mest ta bort med hjälp av sådana operationer?

Lösning:

Först och främst uppskattar vi hur många (eller snarare hur få) pjäser måste verkligen vara kvar på brädet.

Från början har vi 18 diagonaler med ett jämnt antal pjäser, och 20 med ett udda antal pjäser, totalt 38 stycken diagonaler. Vi kallar framöver diagonalerna för ”jämna” och ”udda” beroende på vilket antal pjäser som står på dem för tillfället.

Hur förändras detta antal när vi utför operationer? Jo, vi tar ju bort en pjäs från en jämn diagonal, så den diagonalen kommer att bli udda. Men varje pjäs står på två stycken diagonaler. Så den andra diagonalen kommer också att förändra sort.

Så antingen blir det jämn->udda och udda->jämn, vilket totalt sett inte förändrar antalet udda respektive jämna diagonaler eller så blir det jämn->udda och jämn->udda, vilket minskar antalet jämna diagonaler med 2 och ökar antalet udda diagonaler med 2.

På slutet, när vi inte längre kan utföra några tillåtna operationer, kommer antalet udda diagonaler alltså vara minst 20. Men en udda diagonal kan inte vara tom (för att 0 är ett jämnt antal). Så 20 är det minsta antalet icke-tomma diagonaler på slutet.

Varje pjäs kan bidra till max 2 diagonalers ”icke-tomhet”, vilket betyder att det måste finnas åtminstone 10 pjäser kvar på slutet.

Och det finns ett exempel på hur man kan ta bort pjäser på ett sådant sätt att det blir precis 10 kvar. Notera att om brädet målas schackrutigt, så kommer de vita diagonalerna inte ha något att göra med dem svarta (precis som en löpare alltid måste gå på samma färg under ett schackspel).

Därför om vi ta bort pjäserna från de vita rutorna så att det blir 5 kvar, så kan vi göra detsamma med de svarta rutorna (genom symmetrisk borttagning). Så här kan man ta bort från de vita rutorna, siffrorna nedan anger ordningen: