Algebra – Mattebloggen

Utökad produkt

[kkratings]

Det finns tre tal givna. Om alla tal utökas med 1, så kommer deras produkt också utökas med 1. Om alla tal utökas med 2, så kommer deras produkt också utökas med 2.

Hur mycker ökar produkten med om alla talen ökar med 3?

Visa lösningen

Enligt en broinskription (se bilden nedan) upptäcktes kvaternionerna för exakt 169 år sedan, då William Hamilton tog en promenad i Dublin med sin fru. Hamilton kände till de komplexa talen (till exempel talet $i$ som uppfyller likheten $i\cdot i = -1$ ), men han ville utvidga dem ytterligare till en större talmängd, som fortfarande skulle uppfylla de viktigaste talegenskaperna.

Han kom då på mängden kvaternioner (betecknas $\mathbb{H}$ ), som förutom vanliga tal och $i$ även innehåller talen $j$ och $k$ , som uppfyller följande:

( $i\cdot i = -1$ , denna egenskap är kvar från de komplexa talen)
$j\cdot j = -1$
$k\cdot k = -1$

$i\cdot j = k$
$j\cdot k = i$
$k\cdot i = j$

Det spelar förstås ingen roll vilka bokstäver man väljer att beteckna de här nya talen med, det viktiga är deras egenskaper och samverkan med varandra.

Notera att multiplikationen talen emellan är lite märklig. Desto märkligare är att $i\cdot j$ inte blir samma sak som $j\cdot i$ , det vill säga Hamilton lyckades inte behålla multiplikationens kommutativitet. Man adderar och subtraherar dock kvaternioner precis på samma sätt som man skulle göra med de komplexa talen. Man kan addera de olika bokstäverna med varandra och exempelvis gäller:
$(1+2i+j) + (2+i-j+k) = 3+3i+k$

Hur kan vi lista ut vad $j\cdot i$ bör bli lika med? Tänk på att vi inte kan byta plats på faktorerna, men vi kan multiplicera med något nytt ”från vänster” eller ”från höger”. Säg att vi multiplicerar med $i$ från höger:

$(j\cdot i)\cdot i = j\cdot (i\cdot i) = j\cdot (-1)=-j$

Så att vårt svar multiplicerat med $i$ från höger ska också vara lika med $-j$ . Vad kan det vara för tal?
Om du inte kan komma på det, tänk på vilket tal multiplicerat med $i$ från höger blir lika med $j$ istället och modifiera svaret efter det.

Man kan göra en liten grundmultiplikationstabell för de komplexa talen:

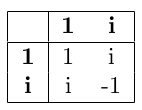
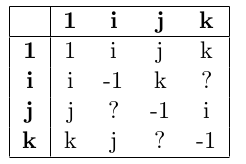
Kan du lista ut vad som står istället för frågtecknen i multiplikationstabellen för kvaternionerna?

En övning i kvaternioner: Vad blir $(1+i+j)(2-j+k)$ ?

Det går att dividera kvaternioner med varandra, resultatet av en division blir alltid ett kvaterniontal (så länge man inte dividerar med 0).

En till övning: Vad blir $1/(i+j)$ för kvaterniontal?

Matematikerns klagan

Vad vore matematiken utan bevis?
Inte riktig matematik, tycker många och artisten Skägget håller med, när han sitter och lider igenom kursen i Sannolikhet och statistik.

Hans senaste låtkreation heter Matematikerns klagan och är en kampsång för ren matematik.

Text och musik: Skägget

Hör upp, bröder, ni matematiker,
på denna min kvalfyllda låt!
Den kursen jag läser mig plågar ihjäl,
ja jag tror snart jag faller i gråt

För det svider i själen, jag dör lite grann
för var sats som går utan bevis,
och när allting jag får är en formel,
det är som gymnasiet gick i repris

Och jag orkar ej mer, nej bespara mig det här,
för jag vet inte ens vad jag gör,
ty i formelhäftet finns svaret
men ingen förklaring varför

Jag finner ett par variabler
som sägs ha nån slags relevans,
och slår upp tio tusen tabeller
för att finna mitt värde nånstans

Så dammar jag av miniräknaren
som jag sen gymnasiet har kvar,
och ger upp alla mina principer
och beräknar numeriskt mitt svar

Men jag orkar ej mer, nej bespara mig det här,
jag vet inte ens varför det går,
men i formelhäftet finns svaret
så jag gör väl precis som det står

Jag som trodde jag var här för att lära mig nåt
– än har jag inte lärt mig ett skvatt!
För vad hjälper en formel jag inte förstått?
Jag ger upp nu och utropar att:

Jag vill va’ en sann matematiker
som bevisar själv allt han vill ha,
och som fäktas mot världens mysterier
med en värja av ren algebra!

Så slut upp bakom mig och vi seglar iväg
på ett stormande renlärigt hav,
med ett skepp som vi bygger från grunden,
med axiomen Euklides oss gav

För jag orkar ej med en till dag av det här,
nej, jag vet inte ens vad jag gör,
ty i formelhäftet finns svaret
men ingen förklaring varför
Ja, i formelhäftet finns svaret,
och matematikern inom mig dör

Den bästa låten om ringar

Jag är stolt över att få presentera låten, som redan är känd för många matematikstuderande vid Uppsala Universitet.

Texten är baserad på innehållet i kursen Algebra II, där mycket ringteori ingår.

Låten heter just Ringteori och stilen är trallpunk.

Text och musik: Erik Svensson

En ring är en mängd och två funktioner,
och som krav ställs på dessa därvid
att det är en abelsk grupp med additionen,
och med gånger en monoid

En ring är en mängd…

Och distributiv ska den vara
men ej tvunget kommutativ, nej!
Exempelvis kvaternioner
och matriser kommuterar ju ej (generellt)

Men antag att den kommuterar,
och att för alla nollskiljda a
finns ett b så att a gånger detta
blir ett, då kallas ringen en kropp, hipp hurra!

För en kropp är så trevligt behändig,
och den har endast två ideal,
varav ena är hela kroppen
och den andra är trivial

En ring är en mängd…

Och mellan två ringar kan hända
att det finns en isomorfi,
då är de i nån mening en enda,
för strukturen bevaras däri

En ring är en mängd…

Klassiska bevis: roten ur 2 irrationellt

Flera av mina bekanta har berättat för mig vad deras första möte med riktiga matematiska bevis var. Och man märker kanske inte först att det man läser eller hör om är så kallade riktiga bevis, förrän man läser ordet ”bevis” explicit. De första sådana för var och en kunde ha varit bevis för Pythagoras sats, något induktionsbevis eller motsägelsebevis.

Här tänkte jag berätta om den mest klassiska klassikern av motsägelsebevis, nämligen att roten ur 2 är ett irrationellt tal.

Vad betyder irrationellt?

Ett irrationellt tal är ett tal som inte går att få med hjälp av naturliga tal 0, 1, 2, 3 …. och de aritmetiska operationerna +, -, * och /. Talen som däremot går att få på det sättet kallas rationella, till exempel $\frac{(5-10)}{3}=\frac{-5}{3}$ . Rationella tal kan alltså skrivas som bråk.

Irrationell och rationell är helt enkelt motsatser. På grund av den här negativa definitionen (det vill säga definiera något genom att använda ett ”inte”), är det naturligt med ett negativt bevis till påståendet (det vill säga motsägelsebevis).

Påstående: $\sqrt2$ är ett irrationellt tal.

Tankegång: Vi skall alltså bevisa att $\sqrt2$ inte är ett rationellt tal. Kan verka svårt först, vi kan ju inte riktigt testa alla möjligheter, alla bråk som överhuvudtaget går att få fram. T.ex. (bara ett exempel nu, helt onödigt för beviset!!!):

Är $\sqrt2=\frac{3}{2}?$ Nej, för då skulle deras kvadrater vara lika $2=\frac{9}{4}$ , vilket absolut inte är sant!

Men det finns oändligt många bråk, vi kan sitta och gissa bråk som är ungefär lika med roten ur 2 och sedan verifiera att de inte är exakt lika. Men bara för att vi inte kan hitta något bevisar inte att det inte finns!

Det är nu vi inser att det faktiskt skulle vara lättare att på något sätt testa alla möjligheter samtidigt. Med det menar jag att vi antar att det finns ett sådant bråk och vi sedan kommer fram till att det aldrig kan bli likhet med roten ur 2. Det är kärnan i alla så kallade motsägelsebevis: antag att det går (antag det positiva påståendet, det utan ”inte”) och kom fram till motsägelse.

Bevis: Antag att roten ur 2 är lika med något bråk. Förkorta bråket så långt det går, så att nämnaren och täljaren inte längre går att dela med samma heltal. Vi har alltså nu:

$\sqrt2=\frac{a}{b}$ och a och b är heltal som inte har någon gemensam delare.

Som förut försöker vi kontrollera likheten genom att kvadrera:

$2=\frac{a^2}{b^2}$ ,

så

$2{b^2}=a^2$ .

Varför är denna likhet omöjligt då? Vi tar hjälp av talteori, läran om heltal och delbarheter.

Vänsterledet $2b^2$ är ett jämnt tal, så högerledet, $a^2$ måste vara det också. Alltså går $a$ att dela med 2, dvs $a=2k$ , där $k$ är ett heltal. Skriv om likheten:

$2{b^2}=(2k)^2=4k^2$ .

MEN detta innebär ju att $b^2=2k^2$ så med samma resonemang som förut får vi att $b$ är ett jämnt tal. Men nu kommer vi fram till motsägelse, eftersom i situtationen då både $a$ och $b$ är jämna går det faktiskt att förkorta bråket (med 2). Nu är vi faktiskt klara.

Vi blev klara så fort vi fick motsägelse i vår lösning. Det är därför det heter motsägelsebevis.

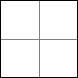
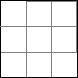
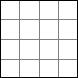
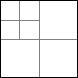
Kvadratuppdelning

Rekommenderad från: 12 år

Visa att en kvadrat kan delas upp i n stycken mindre kvadrater för alla n>5. Med ”att dela upp” menas att vi klipper en kvadrat så att alla erhållna delar också är kvadrater och det blir inga bitar över.

Visa lösning och förklaring

Vi ska hitta på en sådan klippning för alla möjliga antal bitar, från och med 6.

Det känns lite omöljigt, hur ska vi kunna ge en lösning för alla tal som är större än eller lika med 6? Det tar ju oändligt lång tid att presentera! Men, uppgiften säger ”visa att”, det vill säga ”visa att det går” och det frågas inte hur, vilket är två olika saker. Det är skillnad på ”visa att ekvationen har en lösning” och ”bestäm en lösning för ekvationen”. På samma sätt som det är skillnad på ”visa att dinosaurierna levde på Jorden under hundra miljoner år” och ”hitta hundra miljoner årtal under vilka dinosaurierna levde”. Det kan vara subtil olikhet mellan de paren av påståenden, men det är bara så att det senare svaret skulle ge oss det tidigare men inte tvärtom. Man kanske vet att dinosaurierna levde under en viss period, men är osäker på under vilka årtal de säkerligen levde. Men ger någon oss årtal så är det klart att dinosaurierna levde i minst hundra miljoner år.

Men åter till problemet, hur ska man börja lösa det? Tvärtemot vad jag precis skrev om, ska man försöka konstruera lösningarna explicit för olika tal. Vilka n lyckas vi med? Det är en viktig metod i problemlösning, som säger att vi ska starta med små fall, trots att vi har godtyckligt stora framför oss. Små fall kommer ge oss en känsla för hur problemet funkar.

Ok, i hur många kvadrater kan du dela upp en stor kvadrat? Jag kan i 4! Visst, det ingick inte i problemet att lösa det för 4, men jag kan ändå:

kvadrat4

Det går upprepa samma idé och få 9, 16, (och så vidare) kvadrater:

kvadrat9 kvadrat16

Detta ger oss inte så mycket, bara alla kvadrattal, men vi har oändligt många kvar. Vad händer om vi änvänder ”samma konstruktion” som i fallet 4, fast på ett annat sätt? Jag menar så här:

kvadrat7

Och vi kan givetvis fortsätta på samma sätt, splittrande en av kvadraterna i fyra små. Vi kan få 7 kvadrater som på bilden ovan och sedan också 10, 13 osv:

kvadrat10 kvadrat13

Det spelar ingen roll för oss vilken av de befintliga kvaraterna vi delar in i fyra nya. Det viktigaste är att antalet ökar med 3 hela tiden.

Vi har alltså fått svaret för 7, 10, 13, 16, 19, … Oändligt många svar, med det är ändå foftarande oändligt många kvar! Men ni kanske kan gissa att talen 6, 9, 12, 15, …. och talen 8, 11, 14, 17, …. kan fixas på samma sätt så fort vi hittar på någon lösning för 6 respektive 8 kvadrater. Notera då att alla tal större än 6 kommer vara fixade då.

Okej, försök att klura ut 6 eller 8 kvadrater själv innan du tittar nedan. Ett tips är att ha en motsatt taktik: i stället för att lägga till kvadrater till en befintlig konstruktion, försök att ta bort lite kvadrater.

För att få 6 kvarater tar jag bort lite från min konstruktion på 9 kvadrater:

kvadrat9till6 kvadrat6 pil

På liknande sätt gör vi 8 kvadrater från 16:

kvadrat8

Då är vi klara! Vi kan få alla konstruktioner från konstruktionerna med 6, 7 och 8 kvadrater genom att dela upp en kvadrat i fyra och därmed lägga till 3 till antalet.

Vad har då detta med induktion att göra?

Denna lösning, som går ut på metoden ”stegvis konstruering”, kan även anpassas till induktionsmodellen. I det här problemet består inte induktionssteget av ett enda ”steg”, från talet n till talet n+1, utan av tre fall som i och för sig löses på samma sätt (fallen är olika kongruensklasser modulo 3). Basen bestär också av olika fall.

Uppgiften är löst, vi förstår hur lösningen funkar, det är nu vi kan baka in den i induktionsmodellen:

Bas:

n=6, n=7 och n=8:

kvadrat6 kvadrat8

kvadrat7

Induktionssteg:

Induktionsantagandet är att det går att dela upp en stor kvadrat i n stycken mindre. Vi visar att det då går att dela upp i n+3 stycken mindre. Beviset är: skär en av gamla kvadraterna i fyra nya.

Slutsats:

Enligt inuktionsaxiomen och alla basfall modulo 3 visade kan vi dra slutsatsen att påståendet gäller för alla n>5.

Detta kanske inte var det bästa exemplet på att induktion kan vara bra. Lösningen ser mycket naturligare ut i den mindre formella beskrivningen. Men å andra sidan blir den mycket kortare och mer elegant formulerat i induktionstermer.

Induktion (matematisk sådan)

Från Wikipedia: Låt P(n) vara ett påstående som har att göra med ett positivt heltal n, och antag att följande påståenden är sanna:

$P (1)$ är sant.
$\forall p \in \mathbb{N}:P(p) \Rightarrow P(p+1)$ .

Då är påståendet P(n) sant för varje val av det positiva heltalet n.

Lätt som en plätt, eller?

Alla tycker induktion är svårt

Alla som någonsin har varit lärare i grundläggande matematikkurser på universitet har stött på svårigheter inom ett specifikt avsnitt: induktion. Det har skrivits många kompendieinlägg och artiklar i ämnet, det går att hitta massvis med förklaringar och exempel, men ändå har så många så svårt för det. Varje år är det kanske 30 elever man har och 29 av dem har svårigheter med induktion.

Nyligen fick jag ett mail som bad om hjälp med en induktionsuppgift. Problemet för personen var att det inte var en standarduppgift (som handlar om summor, vänsterled=högerled, etc.), och fattar man inte induktionsprincipen då, så är man fast.

Vad induktion inte är

För att börja kasta lite ljus över ämnet, kan jag berätta om vad induktion inte är.

1. Det är inte en metod. Det påminner om en metod väldigt mycket, ”stoppa in basvärden här”, ”skriv induktionsantagandet där”, ”härled induktionssteget mha induktionsantagandet”. Jag tror det är det som förklaringen av induktionsprincipen faller på. Den förklaras mycket formellt, precis som en metod, och därför också uppfattas som sådan. Finns alltså inget sätt att lösa allmännt induktionsproblem!

2. Det är absolut inte en formel. Om man bara har sett summationsuppgifter, säg ”Visa att summan av de första n positiva heltalen är n(n+1)/2” och liknande, tror man kanske att induktionspincipen är en slags formel. Man stoppar in lite summor här och var och blir det likhet, så är man klar. Så är det på sätt och vis med summationsuppgifter, dock faller inte alla de ut lika lätt som exemplet jag tog upp.

3. Det är inte en sats, en teori, en bok, en tupp osv.

Var är det då? Induktionen är en princip, ett axiom och så önskas. Det betyder att det är någonting som vi människor (matematiskt lagda) tycker borde gälla. Det är någonting som följer logikens lagar. Till exempel ”äpplet faller inte långt från trädet” är ett av naturens lagar och det är lite konstigt att titta på det som en metod för beräkning av äpplenas banor. Ett mer matematiskt exempel är ”Om det finns en linje i planet och en punkt utanför linjen, så kan man bara rita en linje genom punkten som är parallell med den första, ändrar man något så kommer första linjen korsas”. Det är ju ganska naturligt att det är så, men det är fortfarande varken metod eller formel.

Hur jag lärde mig induktion

Det skedde relativt tidigt, då jag ännu inte fattade mig på summationstecknet, vilket nog hjälpte för att förstår principen bra (kanske det som är lösningen, lära ut summa efter att man lär ut induktion på grundläggande algebra-kursen?). Jag fick några problem på fritiden, så jag försökte klura ut hur man löste dem. Men det är väldigt svårt att komma på principen själv, så jag lyckades inte först. Sen när man förstår principen så säger det ”klick” och sådana problem löses på bara några minuter.

Och hur förstår man principen då? Jo, genom exempel! Exempel från matten eller vardagen spelar ingen roll. Vitsen är att när någon berättar att man visar någonting att börja med (bas) och sedan visar att ”varje leder till nästa” (induktionssteg), så är det klart att det följer för alla. ”Självklart måste det vara så!”, säger man då, och då har man förstått. Nästa svåra steget är att översätta lösningar till matematikspråket. Just ”översätta”, eftersom mitt största råd är att lösa varje uppgift med ord först, så gott det går, och bara sedan försöka formalisera. Till att börja med: glöm bort vad induktion är och försök lösa de här, så återkommer jag med utförliga exempellösningar.

Etikett: Algebra

Utökad produkt

Utökad produkt

Kvaternioner

Matematikerns klagan

Den bästa låten om ringar

Klassiska bevis: roten ur 2 irrationellt

Kvadratuppdelning

Rekommenderad från: 12 år

Vad har då detta med induktion att göra?

Induktion (matematisk sådan)

Alla tycker induktion är svårt

Vad induktion inte är

Hur jag lärde mig induktion