Jalusimetoden
Min elev Erik har lärt mig hur man multiplicerade stora tal på medeltiden. Uppställningen påminner om hur vi gör nu, men talens enskilda siffror multipliceras i en tabell.
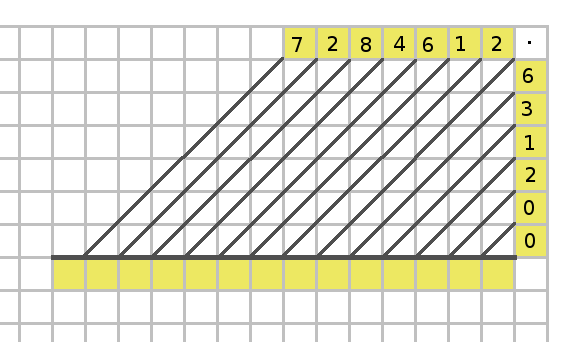
Skriv upp två tal som du vill multiplicera, ena som vanligt från vänster till höger, det andra uppifrån och ned, och gör diagonala streck som på bilden. Produkten ska skrivas in i rutorna längst ner.
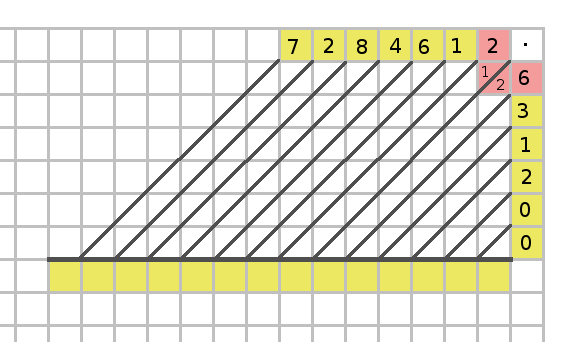
Varje siffra i första talet ska multipliceras med varje siffra i det andra talet. Resultatet skrivs in i rutan som motsvarar kolonnen för första siffran och raden för andra.
Om resultatet är till exempel 2*3=6 så skrivs 0 in i vänstra halvan av rutan och 6 i högra. Man behöver egentligen inte skriva in nollor.
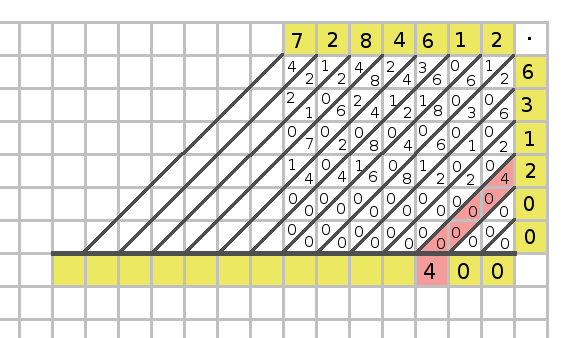
Nu är alla multiplikationer gjorda och det är dags att addera!
Det är därför vi hade sneda linjer, det är längs med dem vi ska addera! Till exempel blir den tredje sneda summan lika med 4.
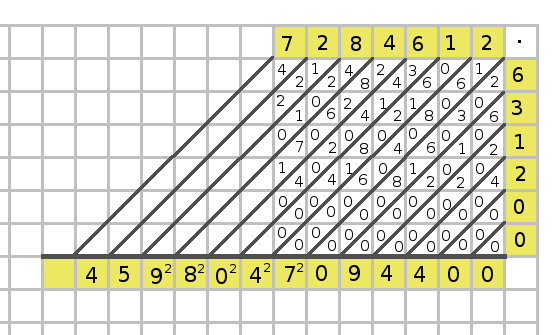
Vi fortsätter att addera från höger till vänster och ibland blir det minnessiffror (i det här exemplet råkade alla minnessiffror vara lika med 2).
Min elev tyckte att det här var det bästa sättet att multiplicera och att han framöver bara skulle utföra sådana här multiplikation!
Vilken multiplikationssätt tycker du bäst om?



Den här metoden är mycket slug och trevlig, men jag vill påpeka att den inte härstammar från medeltiden, utan faktiskt är betydligt äldre än så. Den kalla Jalusimetoden (Gelosia multiplication på engelska) och användes redan ett par tusen år före Kristus, av Indusfolket.
Fin metod. På http://www.youtube.com/watch?v=aD0lp5pzHuM finns en annan som också utnyttjar sneda streck, men med vilken man lättare kan imponera och förvirra bekanta.
Ett annat sätt antt handskas med multiplikation av stora tal var med hjälp av logaritmer. Då log(ab)=loga+logb så kunde man om man ville multiplicera talet a med talet b, först titta i en stor tabell över logaritmer, hitta loga och logb, addera dem och sedan titta vilket tal log(ab) motsvarade i sin tabell då addition var lättare än multiplikation.
Vad jag har förstått så använder man sig av logartimlagarna när man räknar med räknesticka. Det lustiga är att folk var mer effektiva på att få fram svar med räknesticka än vad elever är nu med moderna miniräknare.