Matematiken är full av vackra oväntade kopplingar, som mellan ett träd av bråk och ett gammalt taluppdelningsproblem.
Hittills har vi konstaterat att antalet sätt att dela upp ett tal i en summa av tvåpotenser, där ingen potens förekommer fler än två gånger verkar sammanfalla med täljarna i bråken från Calkin Wilf-trädet, om vi skriver dem på rad. Vi såg också att antalet uppdelningar för ett udda tal är lika med antalet uppdelningar för dess mindre hälft:
#sätt(2n+1) = #sätt(n).
Låt oss hitta något samband för jämna tal. Man kan dela upp ett jämnt tal i tvåpotenser utan att använda några 1:or. Men om man använder 1:or, måste man nödävndigtvis använda exakt 2. Annars skulle inte den totala summan bli jämn.
I det första fallet får vi en summa av typen 2x. I så fall är x en uppdelning för hälften av vårt ursprungliga tal. Exempel: 12 = 2 + 2 + 4 + 4 = 2*(1 + 1 + 2 + 2). En uppdelning för 6 är just 6 = 1 + 1 + 2 + 2.
I det andra fallet får vi 1+1+2x. Då är x uppdelningen för hälften av vårt tal minus ett.
Exempel: 12 = 1 + 1 + 2 + 8 = 1 + 1 + 2*(1 + 4). En uppdelning för 5 är just 5 = 1 + 4.
Vi ser att antalet sätt att dela upp ett jämnt tal motsvarar antalet sätt att dela upp dess hälft samt sätt att dela upp talet ett mindre än dess hälft. Matematiskt sagt får vi
#sätt(2n) = #sätt(n) + #sätt(n – 1).
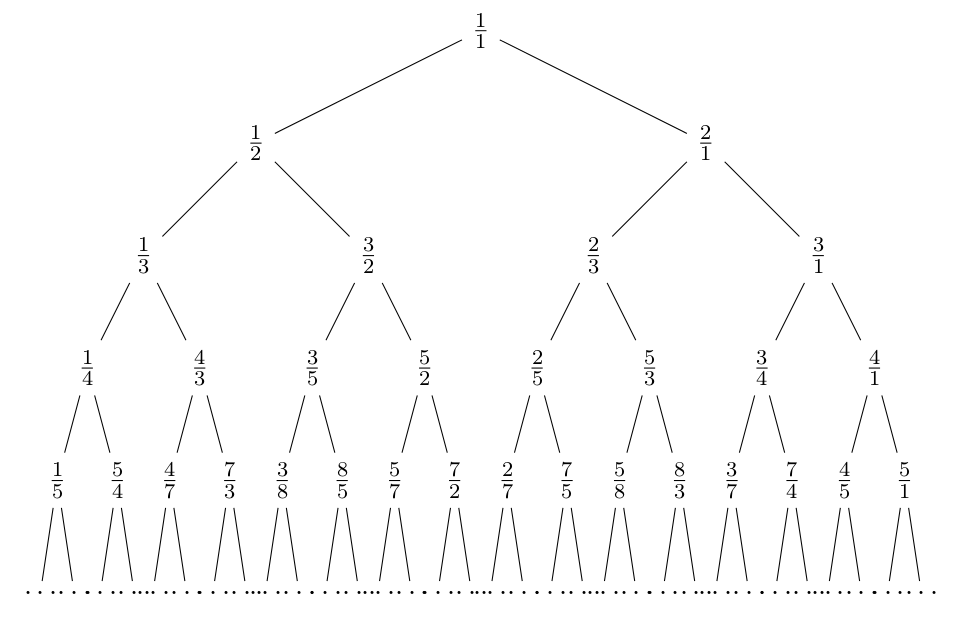
Så varför följer bråkraden samma mönster?
Låt oss numrera varje tal i trädet, motsvarande dess position i raden. Det översta bråket får numret 0, och sedan numrerar vi rad för rad i trädet:
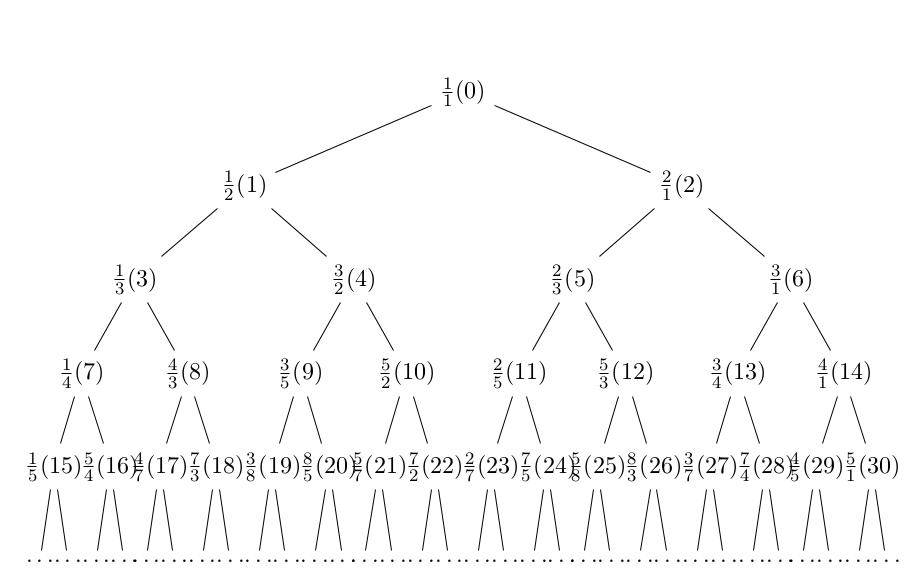
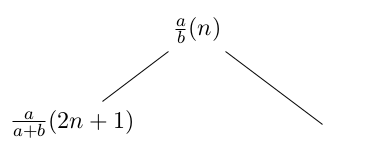
Ett av sambandet vi ser är att varje bråk med udda nummer 2n + 1 är ett vänsterbarn till bråket med nummer n (detta går att visa med induktion). Enligt trädregeln har vänsterbarn exakt samma täljare som sin förälder, därmed följer trädet samma lag som antalet sätt i tvåpotensuppdelningen för udda tal.
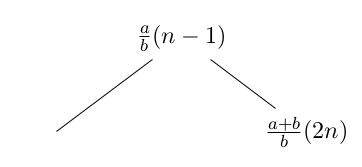
Notera också att varje bråk med jämnt nummer 2n (utom 0) är ett högerbarn till bråket med numret n-1. Men vi har i del 1 visat att att bråket med nästa nummer n kommer att ha samma täljare som bråket innan hade nämnare. Därmed får vi att täljarna a och b tillsammans bildar täljaren a + b, precis som uppdelningssambandet för jämna tal säger.
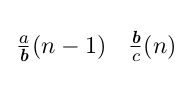
Likheten mellan de två strukturerna är därmed visad. Men det finns fortfarande egenskaper hos Calkin-Wilf trädet som vi inte har pratat om. Till exempel ser vi att inga två bråk upprepar sig. Inget bråk går heller att förkorta. Består trädet rentav av alla icke-förkortningsbara bråk, där varje sådant bråk förekommer exakt en gång?
Om ja, kan du hjälpa mig att bevisa det?