samband – Mattebloggen

Nyligen fyllde jag 28 år vilket är en ”perfekt” ålder på flera sätt :)

Nämligen är 28 det andra perfekta talet, matematiskt sett. Det vill säga, 28 är lika med summan av alla dess delare, exklusive talet självt:

28 = 1 + 2 + 4 + 7 + 14

Det första perfekta talet är 6, det tredje, 496, kommer jag nog inte att fylla…

På antiken kände man till bara fyra perfekta tal, i nuläget har man hittat totalt 48 (senaste talet hittades 2013). Man vet inte om perfekta tal någonsin tar slut. Man vet inte heller om det finns några udda perfekta tal, för alla man hittat hittills är jämna.

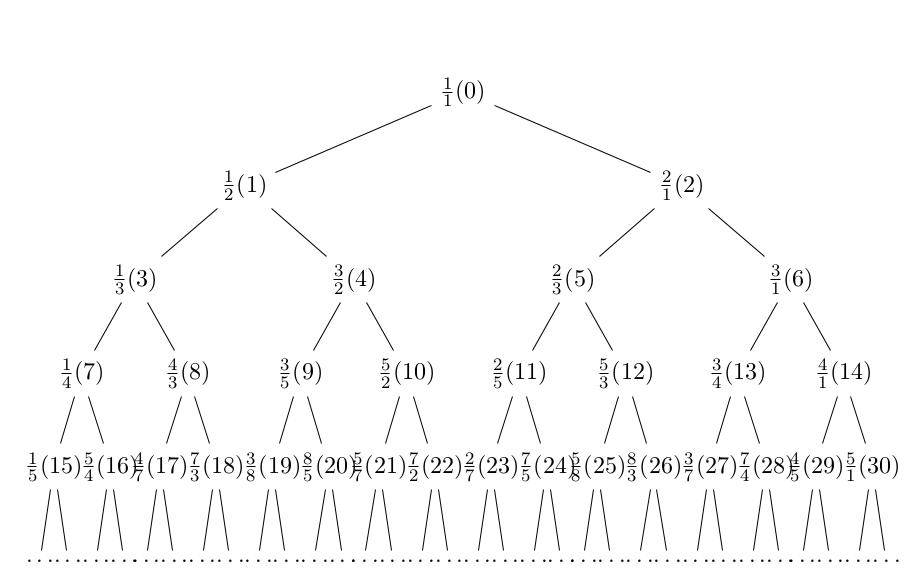
Det lustiga är att man inte hittat mönstret med vilket de perfekta tal förekommer. Men om man skriver perfekta tal i det binära talsystemet så ser det väldigt regelbundet ut:

Perfekt tal i bas 10	I bas 2
6	110
28	11100
496	111110000
8128	1111111000000
33550336	1111111111111000000000000
8589869056	111111111111111110000000000000000
137438691328	1111111111111111111000000000000000000
2305843008139952128	1111111111111111111111111111111000000000000000000000000000000
…	…

Det här verkar rätt kusligt. Varför beter sig perfekta tal binär regelbundet på det här sättet? Alltid med ett primt antal ettor och precis en mindre nolla efter!

Jag tyckte det här var lite alienaktigt och gick in på Wikipedia för att läsa på om perfekta tal. Svaret låg i resultaten om vilka perfekta tal vi hittat fram tills nu.

För det första har vi ju inte hittat några udda perfekta tal. För det andra har redan Euklides visat att om $2^{n}-1$ är ett primtal (kallas för Mersenneprimtal), så är $2^{n-1}(2^{n}-1)$ ett perfekt tal.

Det betyder att så fort ett nytt Mersenneprimtal beräknas, så får vi ett perfekt tal på köpet. Det finns faktiskt exakt 48 hittills kända Mersenneprimtal, precis samma antal som perfekta tal. Detta visar sig inte vara någon slump. Euler visade att alla jämna perfekta tal faktiskt har den här formen, det vill säga motsvarar ett Mersenneprimtal.

Till exempel, 3 är det första Mersenneprimtalet ( $2^2-1$ ) som motsvarar det första perfekta talet $2^1(2^2-1) = 2\cdot3 = 6$ .

Nu är det inte så svårt att bevisa det binära sambandet. $2^{n-1}$ skrivet binärt blir $100...00$ med $n-1$ stycken nollor. $2^{n}-1$ binärt blir $111...11$ med $n$ ettor.
Multiplicerat med varandra blir det såklart $111...1100...00$ med $n$ ettor och $n-1$ nollor. Dessutom är $n$ ett primtal, annars skulle inte talet $2^{n}-1$ vara ett primtal!

Förklaringen på mönstret är klar, men det intressanta är egentligen Euklides och Eulers bevis, som båda lämnas åt läsaren :)

Matematiken är full av vackra oväntade kopplingar, som mellan ett träd av bråk och ett gammalt taluppdelningsproblem.

Hittills har vi konstaterat att antalet sätt att dela upp ett tal i en summa av tvåpotenser, där ingen potens förekommer fler än två gånger verkar sammanfalla med täljarna i bråken från Calkin Wilf-trädet, om vi skriver dem på rad. Vi såg också att antalet uppdelningar för ett udda tal är lika med antalet uppdelningar för dess mindre hälft:

#sätt(2n+1) = #sätt(n).

Låt oss hitta något samband för jämna tal. Man kan dela upp ett jämnt tal i tvåpotenser utan att använda några 1:or. Men om man använder 1:or, måste man nödävndigtvis använda exakt 2. Annars skulle inte den totala summan bli jämn.

I det första fallet får vi en summa av typen 2x. I så fall är x en uppdelning för hälften av vårt ursprungliga tal. Exempel: 12 = 2 + 2 + 4 + 4 = 2*(1 + 1 + 2 + 2). En uppdelning för 6 är just 6 = 1 + 1 + 2 + 2.

I det andra fallet får vi 1+1+2x. Då är x uppdelningen för hälften av vårt tal minus ett.
Exempel: 12 = 1 + 1 + 2 + 8 = 1 + 1 + 2*(1 + 4). En uppdelning för 5 är just 5 = 1 + 4.

Vi ser att antalet sätt att dela upp ett jämnt tal motsvarar antalet sätt att dela upp dess hälft samt sätt att dela upp talet ett mindre än dess hälft. Matematiskt sagt får vi

#sätt(2n) = #sätt(n) + #sätt(n – 1).

Så varför följer bråkraden samma mönster?

Låt oss numrera varje tal i trädet, motsvarande dess position i raden. Det översta bråket får numret 0, och sedan numrerar vi rad för rad i trädet:

Ett av sambandet vi ser är att varje bråk med udda nummer 2n + 1 är ett vänsterbarn till bråket med nummer n (detta går att visa med induktion). Enligt trädregeln har vänsterbarn exakt samma täljare som sin förälder, därmed följer trädet samma lag som antalet sätt i tvåpotensuppdelningen för udda tal.

Notera också att varje bråk med jämnt nummer 2n (utom 0) är ett högerbarn till bråket med numret n-1. Men vi har i del 1 visat att att bråket med nästa nummer n kommer att ha samma täljare som bråket innan hade nämnare. Därmed får vi att täljarna a och b tillsammans bildar täljaren a + b, precis som uppdelningssambandet för jämna tal säger.

Likheten mellan de två strukturerna är därmed visad. Men det finns fortfarande egenskaper hos Calkin-Wilf trädet som vi inte har pratat om. Till exempel ser vi att inga två bråk upprepar sig. Inget bråk går heller att förkorta. Består trädet rentav av alla icke-förkortningsbara bråk, där varje sådant bråk förekommer exakt en gång?

Om ja, kan du hjälpa mig att bevisa det?

Etikett: samband

Perfekta tal och deras binära motsvarigheter

Calkin Wilf-träd, del 3