induktion – Mattebloggen

Andra träffen med Matteklubben, åk 5-6

Matteklubben är Uppsala kommuns satsning på begåvade elever i matematik. Jag har äran att förbereda aktiviteterna som vi håller på med och vara en av lärarna. Du kan kolla upp var vi gjorde på första träffen innan du läser vidare.

36 elever och 6 lärare

Denna gång var det 36 elever som var närvarande, vilket är närmare ett lagom antal än förra gångens 41. Vi var sex stycken lärare och jag tror att vi räckte till det mesta av tiden. Om uppgifterna hade varit för lätta, så skulle vi inte ha så mycket att diskutera med barnen, förutom att de skulle berätta hur de tänkte (och vi skulle förmodligen inte hinna lyssna på allas lösningar). Och om uppgifterna hade varit för svåra så skulle vi inte lärarna ha så mycket att göra annat än att tipsa eleverna om hur de kan tänka. Det är lagom nivå på uppgifter om eleverna löser några, tänker fel på några andra (så att de lär sig något nytt!) och kanske har svårt för att lösa de allra svåraste problemen på egen hand, så att de börjar utbyta idéer med varandra. Vi kunde även lyssna på några elever som inte hittade någon att samarbeta med (eller inte ville samarbeta, vi tvingande ingen att vara i grupp, bara uppmanade). Jag hann i alla fall själv att prata med nästan alla grupper åtminstone en gång, vilket borde betyda att de flesta grupper har hunnit bolla var och en av sin idéer med åtminstone någon av lärarna.

Hemuppgiften

Vi började träffen genom att gå igenom (den frivilliga) läxan. Några av eleverna kom ihåg den och hade jobbat med den hemma, de flesta hade säkert glömt bort den (eller inte jobbat på den). Därför försökte jag föra diskussionen på ett sådant sätt att även de som var helt nya för Matteklubben kunde hänga med lite grann. Vi diskuterade i bara 10 minuter för att de som inte hade fördjupat sig i uppgiften inte skulle bli uttråkade.

Uppgiften som handlar om konkreta tal (5 pärlor, si och så många av varje färg) kunde alla lösa om de försökte. Det handlar om att rita upp och inte glömma något fall. Det fanns ändå flera tolkningar på uppgiften där det fick vara alla möjliga antal svarta pärlor av fem. Några tolkade uppgiften som att armbanden inte fick vara helt svarta eller helt vita. Det gjorde inte så mycket, eftersom man bara behöver lägga till 2 till svaret om dessa armband skulle räknas.

En annan oväntad kuriosa uppstod när jag ritade upp de olika armbanden på den svarta tavlan med en vit krita. Jag tyckte att de pärlorna jag fyllde i var ”svarta”, men många barnen tyckte att dessa var ”vita” (eftersom det verkligen var den färgen de fick). Detta resulterade i ett par intressanta matematiska poänger. Dels att man själv får välja (definiera) vad man kallar för ”svart” och ”vitt”. Och dels att man kan se att det finns lika många armband med 3 svarta och 2 vita pärlor som armband med 2 svarta och 3 vita pärlor, eftersom man kan välja vilken färg man ser som ”svart”.

Vi gick igenom de andra fallen tillsammans: alla svarta, alla vita, 4 svarta + en vit, 4 vita + en svart. Totalt blev det 8 olika armband, om man räknar armband som fås via vridning som samma. Som jag sett av hur eleverna löste läxan, så betraktade de även spegelvända armband som samma (vilket inte var tanken med uppgiften), men detta spelar ingen roll förrän man börjar räkna armband med 7 pärlor.

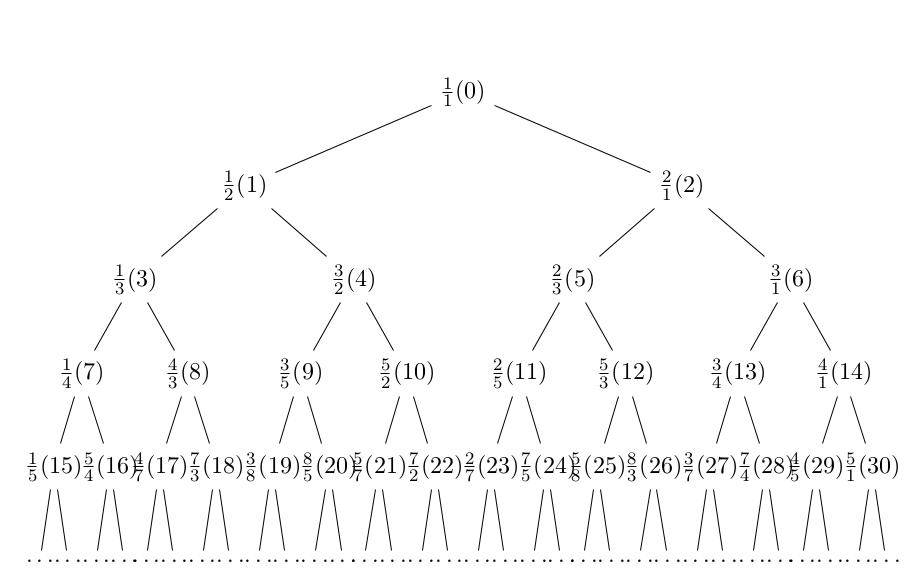
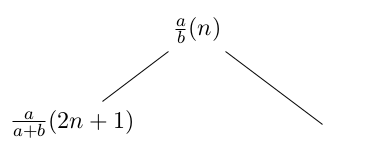
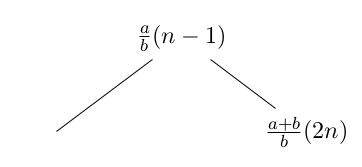
Sista delen av uppgiften var en öppen fråga. Det vara bara 2-3 elever som hade jobbat på det hemma och berättat det för mig. Sambandet för ett godtyckligt antal pärlor är väldigt svårt. Så det var inte tanken att eleverna skulle lösa det, men de kanske kunde upptäcka vissa mönster. Om man inte räknar spegelvända armband som samma, så går uppgiften att lösa med Burnsides Lemma i det generella fallet (vilket är universitetsmatte), och i fall då antalet pärlor i armbandet är ett primtal (p) så är antalet armband lika med

$\frac{2^p-2}{p}+2$

Så till exempel för talet 5 blir svaret:

$\frac{2^5-2}{5}+2 = \frac{32-2}{5}+2 = \frac{30}{5}+2 = 6+2 = 8$

Försök att lista ut var svaret kommer ifrån (tips: 2:an står för antalet färger). Obs! Uppgiften är bara till för de elever som tycker allting annat är jättelätt.

I varianten där spegelvända armband räknas som samma vet jag inte hur man löser uppgiften generellt.

Blandade uppgifter

Sedan löste eleverna blandade uppgiften i ungefär 40 minuter. Vissa satt själva och vissa jobbade i grupper om 2-3. Individuellt arbete är mycket givande, men vi hinner inte jobba med var och en så mycket då antalet elever är så stort. De som räcker upp handen fick dock hjälp snabbt och om de som var villiga att diskutera kunde de få en givande dialog. Exempel på några typiska dialoger skriver jag under varje uppgift.

Om du undrar över lösningen på någon uppgift, så är det bara att fråga i kommentarerna.

Första uppgiften tog längst tid så den diskuterade jag absolut mest med eleverna.

1. a) Matilda har två leksakskuber med bokstäver på sidorna. Totalt finns det 12 olika bokstäver. Hur många ord på två bokstäver kan Matilda bilda?

Lärare: Obs! Låtsasord är också ord i den här uppgiften.
Elever: Får ett ord bestå av två likadana bokstäver?
Lärare: Javisst!

Elever: Det är 6 bokstäver på första kuben och 6 bokstäver på andra. Totalt blir det 6 x 6 = 36 ord.
Lärare: Men måste alltid den första kuben (till exempel den med bokstäverna ABCDEF) alltid stå först? Kan inte den stå på andra platsen?
Elever: Just det, då blir svaret dubbelt så stort!

Elever: Den första bokstaven kan man välja på 12 sätt. Den andra på 11 sätt. Totalt blir det 12 x 11 = 132 ord.
Lärare: Men det är bara en sida man kan välja per kub. Två bokstäver på samma kub bildar inte ett ord.
Elever: Aha, då är det 12 x 6.

Elev: Blir svaret 66?
Lärare: Kanske, hur fick du svaret?
Eleven berättar hur hen tänkte och det visar sig att hen hade tänkt rätt, men räknat fel.
Lärare: Du tänkte rätt!

Det var en del elever som inte noterade att alla de 12 bokstäverna var olika, och därmed snarare löste b)-uppgiften.

1. b) David fick däremot två likadana kuber. Hur många ord på två bokstäver kan han bilda?

Elever: Samma svar som i a), 72 sätt.
Lärare: Låtsas som att vi bara har två bokstäver per kub, A och B på första kuben och likadant på den andra. Vilka ord kan man bygga? T.ex. AA är ett ord.
Elever: Man kan också bygga BB, AB och BA.
Lärare: Så svaret blir…?
Elever: 4 ord.
Lärare: Men om vi skulle tänka som i första uppgiften skulle svaret bli 8 ord. Vad är felet?

2. Det är mörkt i rummet och du vet var det finns en låda med 7 röda och 5 blå pennor. Hur många pennor måste du dra på måfå för att vara säker på att ha minst 2 röda och 3 blå pennor när du sedan kommer ut ur rummet?

Elev: Om man drar 10 pennor, så kan man få 7 röda, men då får man ändå 3 blå.
Lärare: Varför räcker det inte med 9 pennor?
Elev: Man skulle kunna få 7 röda och 2 blå.

3. Vilja räknade fingrarna på sin högra hand: första var tummen, andra – pekfingret, tredje – långfingret, fjärde – ringfingret, femte – lillfingret, sjätte – ringfingret igen, sjunde – långfingret, åttonde – pekfingret, nionde – tummen, tionde – pekfingret och så vidare. Vilket finger blir nummer 2014?

Elever: Vi räknade att pekfingret blir nummer 10, ringfingret nummer 20, ringfingret nummer 30, pekfingret nummer 40, pekfingret nummer 50 och så vidare. Vi räknade ut vad finger nummer 2000 blir och sedan var det bara räkna 14 till. Och det blev ringfingret.
Lärare: Ok, coolt sätt att lösa uppgiften på!

Elev: Nummer 2010 blir pekfingret och sedan spelar det faktiskt ingen roll åt vilket håll man går, om 4 fingrar är det ändå ringfingret.
Lärare: Ja, intressant att man inte behöver bry sig om håll.

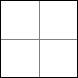
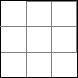
4. Siffrorna 1 till 9 fyller kvadraten som det syns på den vänstra bilden. Man får gå på kvadratens rutor, men aldrig tillbaka till en ruta man varit på förut, och man måste alltid gå till en angränsande ruta.

Emilia gick längs med pilen som syns på den högra bilden. Hon skrev ner siffrorna som hon gick på i ordning och fick talet 84937561. Rita en annan väg, som ger ett större tal (ju större tal, desto bättre).

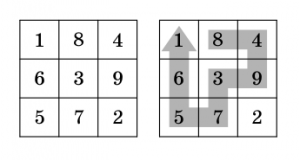
pil_uppgift

Elev: Man måste börja på ett hörn, annars kan man inte gå igenom alla rutor…
Lärare: Kan man inte börja i mitten?
Elev: Men det är ändå lägre!
Lärare: Ja, förvisso.
Elev: Då börjar man med största siffran i hörnet, 5, och sedan går till 7, för 7 är större än 6. Sen går man till 2, för om man går till 3, så kan man inte komma till 2 senare.
Lärare: Kan inte man sluta i 2?
Elev: Jo, kanske, vänta nu lite!…

5. Gustav tänkte på tre tal, men berättade inte vilka tal det var. Däremot sade han vilka olika summor som två av talen kunde bilda: Det var 23, 25 och 28. Vilka tal tänkte Gustav på?

Elev: Jag testade och hittade talet 10, 13 och 15.
Lärare: Kan det ha varit några andra tal han tänkte på som också passar?
Elev: Jag vet inte, jag provade mig fram bara.

Ladda ner för utskrift

Redovisning

Eleverna fick komma fram till tavlan och redovisa sina lösningar, om de ville. Jag försökte att inte lägga ner så mycket tid på det, för då skulle det bli för lite tid kvar till temat. Det vill säga, vi lyssnade på bara en elevlösning per problem.

Intressanta frågor som dök upp (och som jag själv delvis svarade på för att ge exempel på fullständigt resonemang) var:

Problem 2.
– Varför är man säker på att 10 pennor är tillräckligt?
– Man vet att man får 5 röda och 5 blå, eller 6 röda och 4 blå, eller 7 röda och 3 blå. Det är tillräckligt i varje fall.

Problem 4.
– Hur vet man att man måste börja i ett hörn eller mitten med pilen?
– Om man målar kvadraten schackrutigt, så att 5 rutor blir målade (och 4 omålade), så kan man inte starta i en omålad ruta, eftersom man måste hela tiden växla för varje steg:
omålad – målad – omålad – målad – omålad – målad – omålad – målad, vilket gör att man inte kommer att kunna gå på alla 9 rutor.

Problem 5.
(Det har var egentligen ett förtydligande av en annan elevs resonemang).
– Hur vet man att det inte finns något annat svar än 10, 13, 15?
– Om man ökar något tal till exempel, så måste man sänka båda andra och då skulle inte den tredje summan stämma.

Det här resonemanget är inte vattentät kom jag på i efterhand. Om man ökar ett visst tal, så kanske är man inte säker på att det ingår exakt i samma två summor som förut. Till exempel, om vi ökar 15 till 16, så är det inte säkert att 16 ingår i summan 28, utan kanske i de andra två summorna. Det gör att vi inte lika säkert kan förutspå hur de andra två talen måste förändras.

Forskning om area och omkrets

Med dagens tema fick eleverna jobba i grupper om ungefär 4. Det tog inte så lång tid, då frågorna var lite lättare och öppnare än de blandade problemen. De som blev klara fort fick pappret med individuella uppgifter.

Efter ungefär 20 minuter (tror jag) diskuterade vi elevernas förslag på tavlan. Jag skriver under varje uppgift vad vi tog upp i klassdiskussionen.

Figurerna i de här tre uppgifterna får bara ritas längs med rutornas gränser. Inga halva rutor tillåtna det vill säga.

1. Rita så många figurer som möjligt med omkretsen 8 (rutlängder). Vad har de olika figurerna för areor?

Eleverna ritade de två figurerna som består av tre rutor (”pinnen” och ”vinkelhaken”) och en som består av fyra rutor (”fyrkanten” eller ”kvadraten”). En grupp tänkte utanför lådan och hittade på en figur med area 0 (sträckan med längd 4) och med area 2 (två rutor som hänger ihop ett hörn). Jag berättade att figurer som den med arean 0 kallas för ”degenererade figurer” och man bestämmer själv ifall de ska räknas som figurer eller inte (därefter hade vi en omröstning i klassen och majoriteten tyckte inte att de räknades som figurer).

2. Rita så många figurer som möjligt med arean 8 (rutor). Vad har de olika figurerna för omkrets?

Eleverna fick jättemånga olika figurer här, så att de inte ens orkade rita upp alla (jag frågade sedan vilken grupp som hade ritat flest figurer). Omkretsarna var 16, 14, 9, 18.

En av lärarna frågade hur en elev hade fått omkretsen 9. Då ritade eleven upp en kvadrat med ett hål i (också nytänkande!). Omkretsen tyckte eleven var det som var utanpå (hålets omkrets räknades inte med). Men då blev det inte 9, utan 12.

Jag frågade klassen hur läraren kunde misstänka att omkrets nio inte var rätt. En elev svarade att omkrets var tvungen att vara ett jämnt tal. För att det är 4 i början (en ruta) och sedan läggs det liksom på 2 när man bygger ut.

Det blev en liten avvikelse i diskussionen och vi pratade om att omkrets förändras som +2, -2 eller +0 när man bygger ut figuren. Och eftersom det börjar med 4, så förblir det alltid jämnt. Detta är ett mycket djupt resonemang som involverar begrepp som invariant och stegvis konstruktion (början till induktion), som traditionellt är tematik för begåvade elever i högstadiet/gymnasiet. Imponerande att vissa elever i åk 5-6 redan har lite känsla för det!

3. Omkretsen för en viss figur är 20.
a) Vilken är den största arean som figuren kan ha?
b) Vilken är den minsta arean som figuren kan ha?

Kom på så många exempel som möjligt på figurer med störst respektive minst area.

Många av elevgrupperna kom fram till att figuren med störst area var kvadraten med arean 25 och med minst area en avlång rektangel (bredd 1) med arean 9. Jag frågade om de hade fler exempel på figurer med area 9 och det hade de, ”teddybjörn med stort huvud” och ”plusplus” tror jag vi kallade dem:

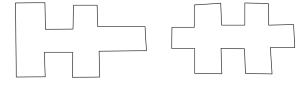
Egentligen funkade många olika lösningar på arean 9 (”böjd pinne” etc.), men med störst area fanns bara kvadraten (som eleverna sade: ”Om det inte får vara en cirkel eller nåt”). Jag sade att man kunde visa det men att det är en för svår uppgift för tillfället.

Ladda ner för utskrift

Förstoring

Precis i slutet pratade vi om vad som hände med arean och omkretsen om en kvadrat får dubbelt så stora sidor. Arean blev 4 gånger så stor! Först tyckte eleverna att omkrets blev 8 gånger så stor (förmodligen för att jag ritade ut de fyra små kvadraterna som den stora består av. Men sedan insåg de att omkretsen blev 2 gånger så stor bara.

Detta gjorde vi för att förstoring och förminskning var vad de individuella uppgifterna handlade om. Dem hann eleverna knappt hålla på med under lektionen, så det blev en (frivillig) läxa.

Tankar efter lektionen

Om möjligt gick lektionen ännu bättre än förra gången. De eleverna som kom för andra gången var de som undervisningen verkligen passade för. Alla gillade aktiviteterna och ingen verkade känna sig så som om denne inte hade där att göra. Mot slutet blev några elever trötta (och började busa lite), så det behövs förmodligen en längre och aktivare rast nästa gång.

Det är roligt att många vågar räcka upp handen och vågar ha fel (även om det är för det mesta samma personer som räcker upp handen om och om igen). Jag har lärt mig 7 av elevnamnen och hoppas att jag ska kunna fånga upp de allra flesta namn vid terminens slut.

Calkin Wilf-träd, del 3

Matematiken är full av vackra oväntade kopplingar, som mellan ett träd av bråk och ett gammalt taluppdelningsproblem.

Hittills har vi konstaterat att antalet sätt att dela upp ett tal i en summa av tvåpotenser, där ingen potens förekommer fler än två gånger verkar sammanfalla med täljarna i bråken från Calkin Wilf-trädet, om vi skriver dem på rad. Vi såg också att antalet uppdelningar för ett udda tal är lika med antalet uppdelningar för dess mindre hälft:

#sätt(2n+1) = #sätt(n).

Låt oss hitta något samband för jämna tal. Man kan dela upp ett jämnt tal i tvåpotenser utan att använda några 1:or. Men om man använder 1:or, måste man nödävndigtvis använda exakt 2. Annars skulle inte den totala summan bli jämn.

I det första fallet får vi en summa av typen 2x. I så fall är x en uppdelning för hälften av vårt ursprungliga tal. Exempel: 12 = 2 + 2 + 4 + 4 = 2*(1 + 1 + 2 + 2). En uppdelning för 6 är just 6 = 1 + 1 + 2 + 2.

I det andra fallet får vi 1+1+2x. Då är x uppdelningen för hälften av vårt tal minus ett.
Exempel: 12 = 1 + 1 + 2 + 8 = 1 + 1 + 2*(1 + 4). En uppdelning för 5 är just 5 = 1 + 4.

Vi ser att antalet sätt att dela upp ett jämnt tal motsvarar antalet sätt att dela upp dess hälft samt sätt att dela upp talet ett mindre än dess hälft. Matematiskt sagt får vi

#sätt(2n) = #sätt(n) + #sätt(n – 1).

Så varför följer bråkraden samma mönster?

Låt oss numrera varje tal i trädet, motsvarande dess position i raden. Det översta bråket får numret 0, och sedan numrerar vi rad för rad i trädet:

Ett av sambandet vi ser är att varje bråk med udda nummer 2n + 1 är ett vänsterbarn till bråket med nummer n (detta går att visa med induktion). Enligt trädregeln har vänsterbarn exakt samma täljare som sin förälder, därmed följer trädet samma lag som antalet sätt i tvåpotensuppdelningen för udda tal.

Notera också att varje bråk med jämnt nummer 2n (utom 0) är ett högerbarn till bråket med numret n-1. Men vi har i del 1 visat att att bråket med nästa nummer n kommer att ha samma täljare som bråket innan hade nämnare. Därmed får vi att täljarna a och b tillsammans bildar täljaren a + b, precis som uppdelningssambandet för jämna tal säger.

Likheten mellan de två strukturerna är därmed visad. Men det finns fortfarande egenskaper hos Calkin-Wilf trädet som vi inte har pratat om. Till exempel ser vi att inga två bråk upprepar sig. Inget bråk går heller att förkorta. Består trädet rentav av alla icke-förkortningsbara bråk, där varje sådant bråk förekommer exakt en gång?

Om ja, kan du hjälpa mig att bevisa det?

Tvåpotenser

Talen på formen $2^n$ dyker upp på många ställen. Finns det en cell som fördubblar sig varje minut, så finns det efter en minut 2 celler. Efter ytterligare en minut finns det 4 celler, sedan 8, sedan 16, 32, 64, 128…

Väldigt ofta dyker även talen på formen $2^n-1$ upp vid problemlösning. $2^{243112609}-1$ är det största hittills kända primtalet till exempel. Men inte alla tal på formen $2^n-1$ är primtal (kan du komma på ett motexempel?).

Försöker du lösa problemet nedan, kommer du upptäcka att de två formerna har mycket med varandra att göra. Fler problem och beskrivningen om hur du vinner oändligt med pengar finns under fliken Cirkel.

Rekommenderad från: 12 år

[kkratings]

Du har 127 enkronorsmynt och 7 tomma plånböcker, och du måste lägga in alla mynten i plånböckerna. Om någon ber dig om
en summa pengar, skall du kunna ge dem några plånböcker, så att det tillsammans i dem finns precis så många kronor som det frågades efter. Hur skall du fördela mynten mellan plånböckerna på så sätt att du kan ge ut vilken summa under 128 kronor som helst utan att öppna dem, om någon ber om det?

Visa lösningen

Eftersom vi kommer att behöva kunna dela ut exakt 1 krona, måste vi även ha en plånbok med exakt 1 krona i, det går ju inte att dela upp beloppet på flera plånböcker.

För att kunna dela ut 2 kronor, lägger vi i 2 kronor i den andra plånboken. Nu kan vi dela ut både 1, 2 och 3 kronor (3 kronor delas ut genom att man ge bort båda plånböckerna).

I den tredje plånboken lägger vi 4 kronor. Nu kan vi dela ut 1,2,3 kronor som förut, samt dela ut plånböcker som förut, men tillsammans med 4 kronor-plånboken: detta ger summor på 1+4,2+4 och 3+4 kronor. Vi kan också dela ut plåboken ensam, vilket ger beloppet 4 kronor. Totalt kan vi dela ut 1,2,3,4,5,6 eller 7 kronor.

Fortsätt på samma sätt: fjärde plånboken får 8 kronor, femte får 16 kronor, sjätte får 32 kronor och sjunde får 64 kronor i sig (antalet kronor i nästa plånbok är alltid lika med nästa tvåpotens). Varför går det att dela ut alla belopp under 128 kronor?

Ett sätt att motivera det är att vårt belopp antingen är större än eller lika med 64 kronor, eller mindre. I det första fallet kommer vi att ge bort plånboken med 64 kronor, i det andra lägger vi undan den för den kommer inte att användas.

Resten av beloppen som ska delas ut är antingen större än eller lika med 32 eller mindre än 32. Dessutom är vi säkra på att det är mindre än 64 kronor (ty sammanlagt var det från början mindre än 128). I det första fallet kommer vi att ge bort plånboken med 32 kronor och i det andra lägga undan den plånboken, för den kommer inte att användas.

Fortsätt på samma sätt att avgöra huruvida vi skall använda nästa (mindre) plånbok eller inte. I det sista steget kommer vi antingen att ha 1 krona eller 0 kronor kvar att dela ut. Antingen ger vi bort plånboken med 1 krona i då, eller så låter vi bli det.

Det strikta beviset för varför detta fungerar är följande:

Från början hade vi mindre än $2^7$ mynt. Vid varje steg har vi mindre än $2^n$ mynt att passa ihop med plånböcker och vi har plånböckerna med värden $1$ , $2^1$ , $2^2$ , … $2^{n-1}$ .

Om antalet mynt vi har kvar att dela ut är mindre än $2^{n-1}$ , så går vi till nästa steg: nu betraktar vi plånböcker med värden $1$ , $2^1$ , $2^2$ , … $2^{n-2}$ och mindre än $2^{n-1}$ kronor att dela ut.

Om antalet mynt vi har kvar att dela ut är större än $2^{n-1}$ , så ger vi bort plånboken med $2^{n-1}$ mynt i. Då har vi kvar mindre än $2^n-2^{n-1}=2^{n-1}$ kronor att dela ut. Och vi har plånböckerna med värden $1$ , $2^1$ , $2^2$ , … $2^{n-2}$ återigen.

I båda fallen reducerade vi n med 1 och kom till en motsvarande situation. Då n=0 blir vi klara, för då har vi kvar mindre än 1 krona att dela ut, det vill säga 0.

Problem vecka 11

Nu kommer de svåraste problemen hittills! Nästa vecka återkommer jag till normal svårighetsgrad.

Skicka in lösningsförslag genom att klicka på länken under uppgifterna senast måndagen den 28 mars. Glöm inte att kolla reglerna och aktuella poängställningen.

Punkter (3 poäng). Sätt ut så många punkter på ett papper som möjligt, på så sätt att ingen trippel av punkter ligger på en och samma linje, utan utgör hörn till en likbent triangel. Du behöver inte bevisa att det inte går att sätta ut fler punkter med samma egenskap.

Likbent triangel

En likbent triangel är en triangel med två lika stora vinklar. En ekvivalent definition är att det är en triangel som har två lika stora sidor.

Här är några exempel:
Likbenta trianglar
Notera att en liksidig triangel är också likbent.

Trasig våg (7 poäng). Du har 3^2k mynt som ser likadana ut, men bland dem finns ett falskt mynt som väger lite mindre än alla andra. Du har också tillgång till tre balansvågar (varje balansvåg har två skålar). Du vet att två vågar är i gott skick, men en är trasig och du vet inte vilken det är. Den trasiga vågen kan visa både jämvikt och ojämvikt åt ena eller andra hållet oberoende av vad du lägger på skålarna.

Hur bestämmer du vilket mynt som är falskt på 3k+1 vägningar?

Visa lösningar

Punkter (Arvids lösning):
Det maximala antalet punkter är 6 i form av en liksidig pentagon (femhörning) med en sjätte punkt mitt i centrum av pentagonen.

Trasig våg (Davids lösning): vi börjar med k=1, alltså 9 mynt och 4 vägningar. Jag ser det som välkänt (för matteintresserade) hur man hittar det falska myntet bland 3^n mynt på n vägningar med en fungerande våg. Observera att om två vågar påstår samma sak så måste påståendet vara sant. Om två vågar motsäger varandra måste en av dessa vara trasig, så den tredje vågen fungerar.

Lägg mynten i 3×3-formation. Väg första raden mot andra i våg 1. Väg första kolumnen mot andra i våg 2. Nu har vi ett misstänkt falskt mynt, i rad A kolumn B säger vi. Vi kan kalla myntet AB :) Vår tredje vägning blir (rad A men inte kolumn B) mot (kolumn B men inte rad A) i våg 3.

Om (rad A men inte kolumn B) visas som lättast: våg 2 säger att falska myntet finns i kolumn B men våg 3 säger att det inte finns i kolumn B. Motsägelsen visar att våg 1 fungerar, falska myntet finns alltså i rad A och med vår sista vägning kan vi hitta det falska myntet bland de tre kandidaterna.

Om (kolumn B men inte rad A) visas som lättast: på samma sätt vet vi att våg 2 fungerar och kan hitta det falska myntet med vår sista vägning.

Om jämvikt visas: det finns tre alternativ på vilka två vågar som fungerar. Om 1 och 2 fungerar är AB såklart falskt. Om 1 och 3 fungerar vet vi att det falska myntet finns i (rad A men inte (rad A men inte kolumn B)), en mängd bestående endast av AB. Om 2 och 3 fungerar får vi också AB som falskt. Alltså måste AB vara falskt och vi har endast använt tre vägningar.

Slutsats: antingen har vi hittat myntet på tre vägningar eller så har vi hittat en fungerande våg och kan använda den för att hitta myntet på den fjärde vägningen. Så för k=2 kan vi stapla mynten i högar om 9. Har vi hittat den falska högen efter tre vägningar så kan vi hitta det falska myntet på resterande 4 vägningar. Annars blir det lätt med hjälp av den fungerande vågen. Vi kan fortsätta med samma princip upp till godtyckligt höga värden på k.

För godtyckligt k=p, stapla i högar om 3^(2p-2). Om vi hittar den falska högen på tre vägningar har vi reducerat problemet till k=p-1. Annars har vi en fungerande våg, vi har 3p-2 vägningar kvar (vilket är större än 2p för p>2) och 3^(2p) mynt att väga = lätt.

Lösningen till problemet för de äldre vecka 37

Mattegåta

Fredrik och Mona har 1999 kronor i kontanter tillsammans och ingen av dem har några tjugolappar (de har alltså bara valörerna 1, 5, 10, 50, 100, 500, 1000 kronor). Fredrik ska köpa grisen i säcken av Mona och Mona tar inte kort. Grisen i säcken kostar ett helt antal kronor och det är inte mer än vad Fredrik har i cash.

Visa att Fredrik garanterat kan köpa grisen i säcken och få rätt summa i växel.

Diskussion

Det har kommit in två lösningar, som är ganska olika. Den första lösningen undersöker vad det kan finnas för valörer och sammanfattar allting i ett enda fall. Den andra lösningen säger inget om de konkreta valörerna, utan baserar sig på induktion. Välj själva vilken ni tycker bäst om!

Lösning 1 (av Erik Svensson)

Antag att Mona och Fredrik, av till synes måhända besynnerliga skäl, beslutar att Mona först av allt lånar ut alla sina pengar till Fredrik. Då vet vi att Fredrik har totalt 1999 kronor, och att han nu ska betala till Mona en viss summa pengar, som är summan av grispriset och pengarna han just lånat. Denna summa överstiger inte 1999 kronor, eftersom grisen kostade högst det Fredrik hade från början, vilket tillsammans med Monas pengar alltså blir högst den totala mängden pengar i rörelse, dvs 1999 kr.

Vi har därmed reducerat problemet till att handla om huruvida Fredik kan skriva varje tal under 2000 som en summa av de kontantvalörer som finns tillgängliga.

Låt oss studera fallet där Fredik har så många stora valörer som möjligt. Vi noterar att om han klarar det i det fallet, så går det även i alla andra fall, ty att byta ut en stor valör mot flera mindre kan uppenbart inte reducera antalet möjliga summor.

Fallet med maximala valörer är att Fredik innehar följande kontanter:

1x 1000 kr
1x 500 kr
4x 100 kr
1x 50 kr
4x 10 kr
1x 5 kr
4x 1 kr

Det är lätt att visa att varje tal under 2000 kan skrivas som en summa av ovanstående valörer. Varje tal 1-9 kan ju skrivas med bara enkronor för talen 1-4, med en femkrona för 5 och med en femkrona och resten enkronor för 6-9. På exakt samma sätt kan varje tiotal upp till hundra nås, och inom varje sånt tiotal kan vi nå varje ental med en- och femkronorna. På samma sätt kan vi även nå alla hundratal med 100- och 500-lapparna, och inom varje hundratal når vi varje 10-tal med 10- och 50-kronorna, och inom varje tiotal inom varje hundratal når vi varje ental med hjälp av 1- och 5-kronorna. Därmed kan varje tal upp till 1000 skrivas. Och vill vi ha varje tal upp till 2000 så lägger vi bara till 1000-lappen där den behövs.

Således kommer Fredik kunna betala Mona exakt rätt mängd pengar, vilket skulle bevisas.

Lösning 2 (av Johan Björklund)

Vi gör detta med induktion. Om Fredrik har 0 kr så är grisen gratis och vi är klara.

Antag att Fredrik kan köpa grisen om Fredrik har p kronor (och griskostnaden är ≤p). Om Fredrik har p+1>0 kronor så kan han givetvis köpa den om grisen är gratis. Om den inte är gratis så försöker han betala en krona.

Antag att den lägsta valören Fredrik har är m. Då gäller att 1999≡m-1 (mod m) då alla valörer delar 2000. Då varje valör delar ”nästa” valör så måste det då vara så att det finns m-1 kronor i lägre valörer (fördelat mellan Mona och Fredrik).

Men då Fredrik hade lägsta valör m så måste alla de m-1 kronorna tillhöra Mona. Om Fredrik ger sin m-sedel till Mona och får de m-1 kronorna tillbaka så har han p kronor kvar och har betalat av 1 krona på grisen, dvs vi är i det tidigare lösta fallet. Induktion ger att han alltid kan betala.

Kvadratuppdelning

Rekommenderad från: 12 år

Visa att en kvadrat kan delas upp i n stycken mindre kvadrater för alla n>5. Med ”att dela upp” menas att vi klipper en kvadrat så att alla erhållna delar också är kvadrater och det blir inga bitar över.

Visa lösning och förklaring

Vi ska hitta på en sådan klippning för alla möjliga antal bitar, från och med 6.

Det känns lite omöljigt, hur ska vi kunna ge en lösning för alla tal som är större än eller lika med 6? Det tar ju oändligt lång tid att presentera! Men, uppgiften säger ”visa att”, det vill säga ”visa att det går” och det frågas inte hur, vilket är två olika saker. Det är skillnad på ”visa att ekvationen har en lösning” och ”bestäm en lösning för ekvationen”. På samma sätt som det är skillnad på ”visa att dinosaurierna levde på Jorden under hundra miljoner år” och ”hitta hundra miljoner årtal under vilka dinosaurierna levde”. Det kan vara subtil olikhet mellan de paren av påståenden, men det är bara så att det senare svaret skulle ge oss det tidigare men inte tvärtom. Man kanske vet att dinosaurierna levde under en viss period, men är osäker på under vilka årtal de säkerligen levde. Men ger någon oss årtal så är det klart att dinosaurierna levde i minst hundra miljoner år.

Men åter till problemet, hur ska man börja lösa det? Tvärtemot vad jag precis skrev om, ska man försöka konstruera lösningarna explicit för olika tal. Vilka n lyckas vi med? Det är en viktig metod i problemlösning, som säger att vi ska starta med små fall, trots att vi har godtyckligt stora framför oss. Små fall kommer ge oss en känsla för hur problemet funkar.

Ok, i hur många kvadrater kan du dela upp en stor kvadrat? Jag kan i 4! Visst, det ingick inte i problemet att lösa det för 4, men jag kan ändå:

kvadrat4

Det går upprepa samma idé och få 9, 16, (och så vidare) kvadrater:

kvadrat9 kvadrat16

Detta ger oss inte så mycket, bara alla kvadrattal, men vi har oändligt många kvar. Vad händer om vi änvänder ”samma konstruktion” som i fallet 4, fast på ett annat sätt? Jag menar så här:

kvadrat7

Och vi kan givetvis fortsätta på samma sätt, splittrande en av kvadraterna i fyra små. Vi kan få 7 kvadrater som på bilden ovan och sedan också 10, 13 osv:

kvadrat10 kvadrat13

Det spelar ingen roll för oss vilken av de befintliga kvaraterna vi delar in i fyra nya. Det viktigaste är att antalet ökar med 3 hela tiden.

Vi har alltså fått svaret för 7, 10, 13, 16, 19, … Oändligt många svar, med det är ändå foftarande oändligt många kvar! Men ni kanske kan gissa att talen 6, 9, 12, 15, …. och talen 8, 11, 14, 17, …. kan fixas på samma sätt så fort vi hittar på någon lösning för 6 respektive 8 kvadrater. Notera då att alla tal större än 6 kommer vara fixade då.

Okej, försök att klura ut 6 eller 8 kvadrater själv innan du tittar nedan. Ett tips är att ha en motsatt taktik: i stället för att lägga till kvadrater till en befintlig konstruktion, försök att ta bort lite kvadrater.

För att få 6 kvarater tar jag bort lite från min konstruktion på 9 kvadrater:

kvadrat9till6 kvadrat6 pil

På liknande sätt gör vi 8 kvadrater från 16:

kvadrat8

Då är vi klara! Vi kan få alla konstruktioner från konstruktionerna med 6, 7 och 8 kvadrater genom att dela upp en kvadrat i fyra och därmed lägga till 3 till antalet.

Vad har då detta med induktion att göra?

Denna lösning, som går ut på metoden ”stegvis konstruering”, kan även anpassas till induktionsmodellen. I det här problemet består inte induktionssteget av ett enda ”steg”, från talet n till talet n+1, utan av tre fall som i och för sig löses på samma sätt (fallen är olika kongruensklasser modulo 3). Basen bestär också av olika fall.

Uppgiften är löst, vi förstår hur lösningen funkar, det är nu vi kan baka in den i induktionsmodellen:

Bas:

n=6, n=7 och n=8:

kvadrat6 kvadrat8

kvadrat7

Induktionssteg:

Induktionsantagandet är att det går att dela upp en stor kvadrat i n stycken mindre. Vi visar att det då går att dela upp i n+3 stycken mindre. Beviset är: skär en av gamla kvadraterna i fyra nya.

Slutsats:

Enligt inuktionsaxiomen och alla basfall modulo 3 visade kan vi dra slutsatsen att påståendet gäller för alla n>5.

Detta kanske inte var det bästa exemplet på att induktion kan vara bra. Lösningen ser mycket naturligare ut i den mindre formella beskrivningen. Men å andra sidan blir den mycket kortare och mer elegant formulerat i induktionstermer.

Induktion (matematisk sådan)

Från Wikipedia: Låt P(n) vara ett påstående som har att göra med ett positivt heltal n, och antag att följande påståenden är sanna:

$P (1)$ är sant.
$\forall p \in \mathbb{N}:P(p) \Rightarrow P(p+1)$ .

Då är påståendet P(n) sant för varje val av det positiva heltalet n.

Lätt som en plätt, eller?

Alla tycker induktion är svårt

Alla som någonsin har varit lärare i grundläggande matematikkurser på universitet har stött på svårigheter inom ett specifikt avsnitt: induktion. Det har skrivits många kompendieinlägg och artiklar i ämnet, det går att hitta massvis med förklaringar och exempel, men ändå har så många så svårt för det. Varje år är det kanske 30 elever man har och 29 av dem har svårigheter med induktion.

Nyligen fick jag ett mail som bad om hjälp med en induktionsuppgift. Problemet för personen var att det inte var en standarduppgift (som handlar om summor, vänsterled=högerled, etc.), och fattar man inte induktionsprincipen då, så är man fast.

Vad induktion inte är

För att börja kasta lite ljus över ämnet, kan jag berätta om vad induktion inte är.

1. Det är inte en metod. Det påminner om en metod väldigt mycket, ”stoppa in basvärden här”, ”skriv induktionsantagandet där”, ”härled induktionssteget mha induktionsantagandet”. Jag tror det är det som förklaringen av induktionsprincipen faller på. Den förklaras mycket formellt, precis som en metod, och därför också uppfattas som sådan. Finns alltså inget sätt att lösa allmännt induktionsproblem!

2. Det är absolut inte en formel. Om man bara har sett summationsuppgifter, säg ”Visa att summan av de första n positiva heltalen är n(n+1)/2” och liknande, tror man kanske att induktionspincipen är en slags formel. Man stoppar in lite summor här och var och blir det likhet, så är man klar. Så är det på sätt och vis med summationsuppgifter, dock faller inte alla de ut lika lätt som exemplet jag tog upp.

3. Det är inte en sats, en teori, en bok, en tupp osv.

Var är det då? Induktionen är en princip, ett axiom och så önskas. Det betyder att det är någonting som vi människor (matematiskt lagda) tycker borde gälla. Det är någonting som följer logikens lagar. Till exempel ”äpplet faller inte långt från trädet” är ett av naturens lagar och det är lite konstigt att titta på det som en metod för beräkning av äpplenas banor. Ett mer matematiskt exempel är ”Om det finns en linje i planet och en punkt utanför linjen, så kan man bara rita en linje genom punkten som är parallell med den första, ändrar man något så kommer första linjen korsas”. Det är ju ganska naturligt att det är så, men det är fortfarande varken metod eller formel.

Hur jag lärde mig induktion

Det skedde relativt tidigt, då jag ännu inte fattade mig på summationstecknet, vilket nog hjälpte för att förstår principen bra (kanske det som är lösningen, lära ut summa efter att man lär ut induktion på grundläggande algebra-kursen?). Jag fick några problem på fritiden, så jag försökte klura ut hur man löste dem. Men det är väldigt svårt att komma på principen själv, så jag lyckades inte först. Sen när man förstår principen så säger det ”klick” och sådana problem löses på bara några minuter.

Och hur förstår man principen då? Jo, genom exempel! Exempel från matten eller vardagen spelar ingen roll. Vitsen är att när någon berättar att man visar någonting att börja med (bas) och sedan visar att ”varje leder till nästa” (induktionssteg), så är det klart att det följer för alla. ”Självklart måste det vara så!”, säger man då, och då har man förstått. Nästa svåra steget är att översätta lösningar till matematikspråket. Just ”översätta”, eftersom mitt största råd är att lösa varje uppgift med ord först, så gott det går, och bara sedan försöka formalisera. Till att börja med: glöm bort vad induktion är och försök lösa de här, så återkommer jag med utförliga exempellösningar.

36 elever och 6 lärare

Hemuppgiften

Blandade uppgifter

Redovisning

Forskning om area och omkrets

Förstoring

Tankar efter lektionen

Vill du få extrainfo om problemlösning via e-post från Mattebloggen?

Rekommenderad från: 12 år

Likbent triangel

Visa lösningar

Mattegåta

Diskussion

Lösning 1 (av Erik Svensson)

Lösning 2 (av Johan Björklund)

Rekommenderad från: 12 år

Vad har då detta med induktion att göra?

Alla tycker induktion är svårt

Vad induktion inte är

Hur jag lärde mig induktion