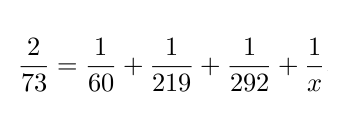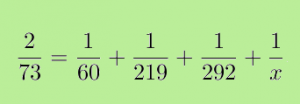bråk – Mattebloggen

Sju fikabröd

[kkratings]

Hur kan man dela sju likadana wienerbröd rättvist mellan 12 personer utan att dela upp något bröd i 12 eller fler delar?

Visa lösningen

Två delat med två

[kkratings]

Bråkuppställningen på bilden är lite konstig, eftersom det inte går att tyda vad som ska delas med vad i vilken ordning. Du får göra bråkstrecken olika långa för att kunna räkna ut resultatet.

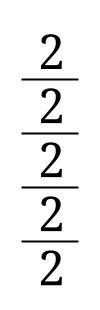
22222

Hur många olika resultat går det att få på det sättet? Vilka är de möjliga svaren?

Visa lösningen

Aktiviteten trassel

Rekommenderas för: gymnasieet, universitetet (eller i förenklad form för högstadiet)

Materiel: två stora rep eller sladdar (gärna av olika färger), en ogenomskinlig plastpåse

Tid: 45 minuter

Antalet deltagare: 4 + publik

Aktiviteten ”trassel” kommer från matematikern och pusselkonstruktören Johan Conway och har genomförts i Sverige på bland annat Sonja Kovalevsky-dagarna. Den passar att genomföra på en matematiklektion om bråkräkning/gruppteori eller som en extra matematikaktivitet.

Man börjar med att fyra elever ställer sig som hörnen på en kvadrat inför resten av klassen. Var och en av dem tar tag i var sin ände av ett rep så att repen hänger parallella med hur publiken sitter. Under experimentet får de aldrig släppa sin ände.

Så här ser det ut uppifrån (Positionerna närmast klassen är D och C):

trassel start

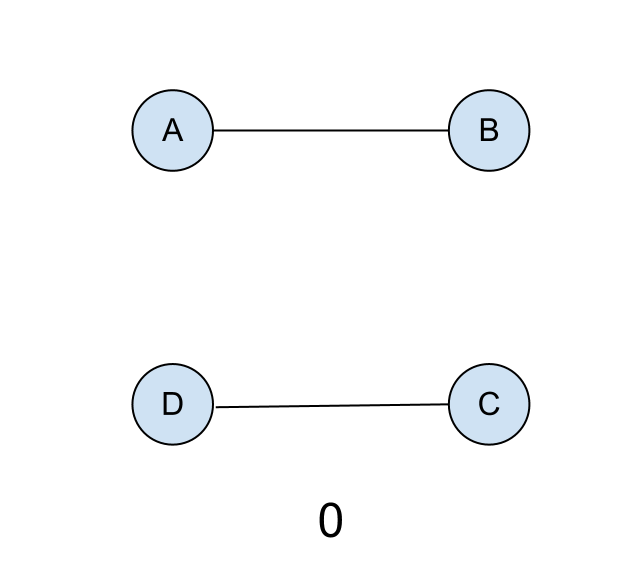
Nu kommer de fyra personerna utföra en slags dans och trassla till repen samtidigt. Varje trassel (tangle) repen bildar kommer att ha ett motsvarande tal. Från början, när repen är parallella mot varandra och mot klassen, motsvarar det talet 0.

Det första tillåtna danssteget är att vrida om repen runt varandra. Och inte på vilket sätt som helst, utan det måste göras av personerna som står på positionerna B och C. Dessa två personer byter plats med varandra och B är den som lyfter sin repände, som C går under för att komma till sin nya position.

vrida om

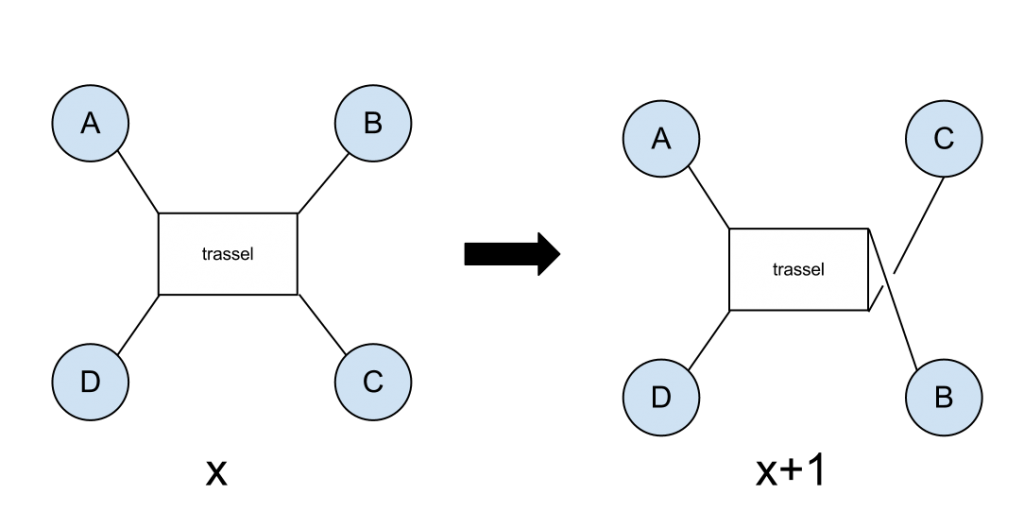
Att vrida om trasslet på det här sättet kommer att öka talet med 1. Så en omvridning ger ett trassel med värdet 1, medan en till omvridning ger talet 2 osv.

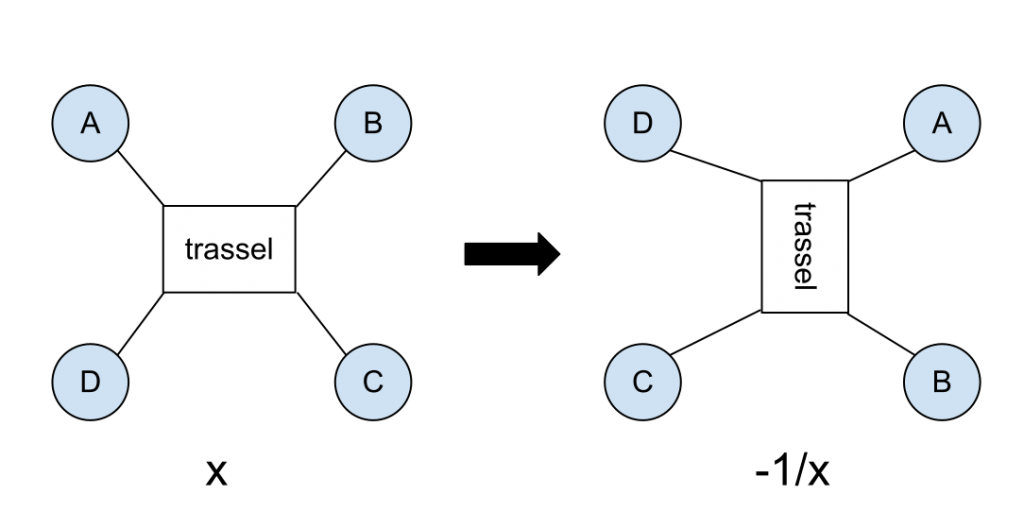
Det andra tillåtna danssteget är att rotera medurs. Person A går till position B, person B går till position C och så vidare.

Att rotera trasslet kommer också att förändra talet. Men hur? Om elevera har hållit på med funktioner och algebra tidigare kan man låta dem att lista ur svaret. Annars kan man helt enkelt säga att talet x omvandlas till talet -1/x vid en sådan rotation. Notera t.ex. att två rotationer i rad inte gör någon skillnad på trasslet, vilket är klart för trassel som består av några omvridningar:

n -> -1/n -> -(1/(-1/n)) = n

rotera

När alla har förstått reglerna kan man be eleverna att uföra några danssteg (börja med att först
vrida om), samtidigt som man räknar på talet som ska motsvara trasslet. Om man från början gör dansstegen: vrida om, vrida om, rotera, vrida om, vrida om, vrida om, rotera, vrida om så kommer man till talet:

0 -> 1 -> 2 -> -1/2 -> 1/2 -> 3/2 -> 5/2 -> -2/5 -> 3/5

Hur ska man lösa upp detta trassel om man bara tillåts att göra dansstegen ovan? Publiken får lösa denna uppgift genom att försöka räkna ut hur man ska göra med bråket 3/5 för att det ska bli 0, om man bara tillåts addera 1 och ta den negativa inversen. Man kan ju inte göra dansstegen ”baklänges”, eftersom steget ”att vrida runt åt andra hållet” inte finns.

När någon har kommit på dansstegsföljden kan man testa dansen och se att knuten verkligen löses upp.

Det här kan man göra med andra tal. Ju svårare trasslet är, desto roligare blir det att se det lösas upp. När repen är tilltrasslade, kan man knyta några plastpåsar runt dem, så att trasslet inte syns och sedan utföra dansstegen som eventuellt ska lösa upp trasslet. När talet på tavlan är 0 kan man knyta upp påsarna och se att allt blir som i början, bara man drar i repen!

Fler frågor att diskutera på avancerad nivå:

– Vad händer om man roterar först? Vad är talet -1/0 och vad har det för egenskaper? Ska trasslet -1/0 förändras om man vrider om det?

– Hitta inversen till att vrida om. Det vill säga, om man startar från ett trassel och sedan vrider om en gång, vad för danssteg skall man göra för att komma tillbaka till starttrasslet?

Fler frågor för att grupper:

– Om man börjar från 0, hur kommer man till ett specifikt trassel, t.ex. -3?

– Hut kommer man snabbast ner till 0 från ett specifikt trassel? Här kan eleverna tävla om vem som kan hitta på kortaste dansstegsekvensen när trasslet är ett relativt avancerat bråktal.

Mer om aktiviteten kan du läsa i Conways text (tangles börjar på sida 10) conway.pdf, samt Tom Davis text med utförlig diskussion och beskrivning av aktiviteten. tangle.pdf.

Tack till Johan Björklund för tipset!

Calkin Wilf-träd, del 3

Matematiken är full av vackra oväntade kopplingar, som mellan ett träd av bråk och ett gammalt taluppdelningsproblem.

Hittills har vi konstaterat att antalet sätt att dela upp ett tal i en summa av tvåpotenser, där ingen potens förekommer fler än två gånger verkar sammanfalla med täljarna i bråken från Calkin Wilf-trädet, om vi skriver dem på rad. Vi såg också att antalet uppdelningar för ett udda tal är lika med antalet uppdelningar för dess mindre hälft:

#sätt(2n+1) = #sätt(n).

Låt oss hitta något samband för jämna tal. Man kan dela upp ett jämnt tal i tvåpotenser utan att använda några 1:or. Men om man använder 1:or, måste man nödävndigtvis använda exakt 2. Annars skulle inte den totala summan bli jämn.

I det första fallet får vi en summa av typen 2x. I så fall är x en uppdelning för hälften av vårt ursprungliga tal. Exempel: 12 = 2 + 2 + 4 + 4 = 2*(1 + 1 + 2 + 2). En uppdelning för 6 är just 6 = 1 + 1 + 2 + 2.

I det andra fallet får vi 1+1+2x. Då är x uppdelningen för hälften av vårt tal minus ett.
Exempel: 12 = 1 + 1 + 2 + 8 = 1 + 1 + 2*(1 + 4). En uppdelning för 5 är just 5 = 1 + 4.

Vi ser att antalet sätt att dela upp ett jämnt tal motsvarar antalet sätt att dela upp dess hälft samt sätt att dela upp talet ett mindre än dess hälft. Matematiskt sagt får vi

#sätt(2n) = #sätt(n) + #sätt(n – 1).

Så varför följer bråkraden samma mönster?

Låt oss numrera varje tal i trädet, motsvarande dess position i raden. Det översta bråket får numret 0, och sedan numrerar vi rad för rad i trädet:

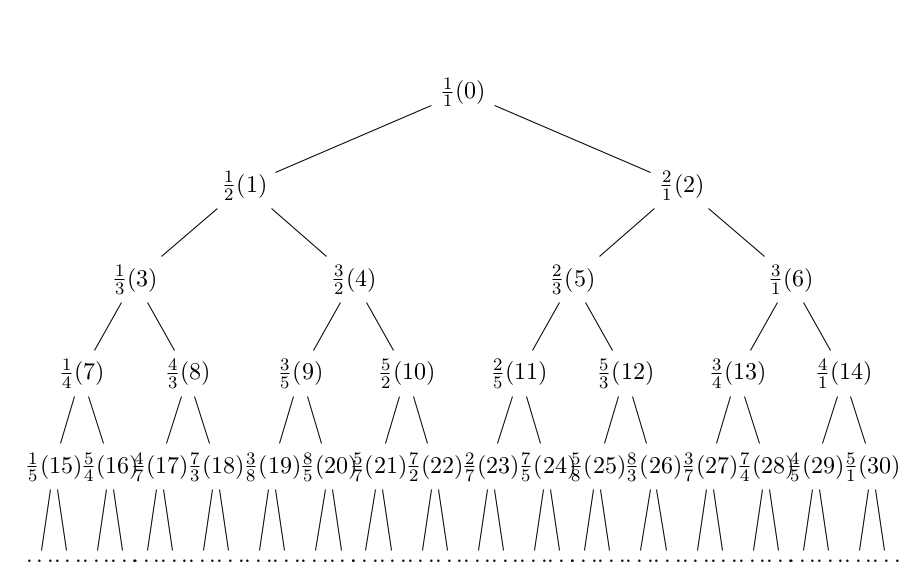
Ett av sambandet vi ser är att varje bråk med udda nummer 2n + 1 är ett vänsterbarn till bråket med nummer n (detta går att visa med induktion). Enligt trädregeln har vänsterbarn exakt samma täljare som sin förälder, därmed följer trädet samma lag som antalet sätt i tvåpotensuppdelningen för udda tal.

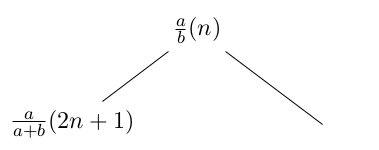
Notera också att varje bråk med jämnt nummer 2n (utom 0) är ett högerbarn till bråket med numret n-1. Men vi har i del 1 visat att att bråket med nästa nummer n kommer att ha samma täljare som bråket innan hade nämnare. Därmed får vi att täljarna a och b tillsammans bildar täljaren a + b, precis som uppdelningssambandet för jämna tal säger.

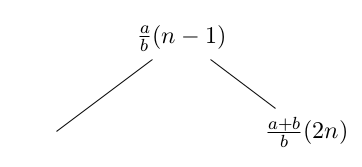
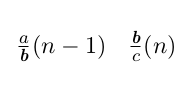
Likheten mellan de två strukturerna är därmed visad. Men det finns fortfarande egenskaper hos Calkin-Wilf trädet som vi inte har pratat om. Till exempel ser vi att inga två bråk upprepar sig. Inget bråk går heller att förkorta. Består trädet rentav av alla icke-förkortningsbara bråk, där varje sådant bråk förekommer exakt en gång?

Om ja, kan du hjälpa mig att bevisa det?

Calkin Wilf-träd, del 1

Det är sällan som nya matematiska upptäckter handlar om någonting enkelt. All matematik som lärs ut i grundskolan upptäcktes för länge sedan av gamla greker, araber, kineser och indier. Gymnasiematematiken baserar sig på upptäckter som är minst 300 år gamla. Den nyaste forskningen är även för svår för universitetsmatten: algebrakurser har exempelvis varit ungefär likadana sedan 1920-talet.

Just därför är det så imponerande när nya enkla samband hittas. Calkin och Wilf publicerade en artikel om följande struktur så sent som 2000. Likt Pascals oändliga triangel, introducerar de ett oändligt träd, med nu är noderna bråktal.

Börja med att skriva 1/1 högst upp.
Sedan upprepa samma process om och om igen: om ett tal a/b är med i trädet, rita ut två grenar från det och skriv bråket a/(a+b) i den vänstra grenen och (a+b)/b i den högra. Till exempel, så kommer 1/1 att förgrenas i 1/2 samt 2/1.
1/2 kommer att förgrenas i 1/3 samt 3/2, och så vidare. Vi får följande struktur, som bär namnet Calkin Wilf-trädet:

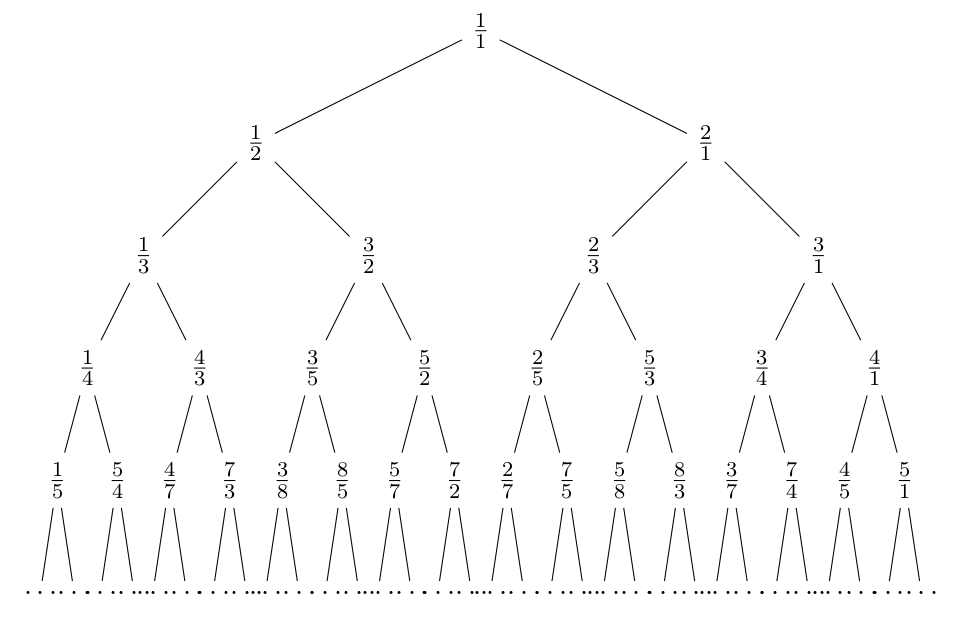
Låt oss skriva ner bråken genom att läsa av en rad i trädet i taget. Vi får listan:

$\frac{1}{1}, \frac{1}{2}, \frac{2}{1}, \frac{1}{3}, \frac{3}{2}, \frac{2}{3}, \frac{3}{1}, \frac{1}{4}, \frac{4}{3}, \frac{3}{5}, \frac{5}{2}, \frac{2}{5}, \frac{5}{3}, \frac{3}{4}, \frac{4}{1}, \frac{1}{5}, \frac{5}{4}, \frac{4}{7}, \frac{7}{3}, \frac{3}{8}, \frac{8}{5}, \frac{5}{7}, \frac{7}{2}, \frac{2}{7}, \frac{7}{5}, \frac{5}{8}, \frac{8}{3}, \frac{3}{7}, \frac{7}{4}, \frac{4}{5}, \frac{5}{1}, \ldots$

Notera att varje bråks nämnare sammanfaller med nästa bråks täljare. Varför är det alltid så?

För två grannar i trädet är egenskapen inte alls konstig, eftersom båda talen sammanfaller med a+b. Men om två tal är bredvid varandra i trädet utan att vara omedelbara grannar, så är det ena någons högergranne, medan det andra någons vänstergranne. Notera att högergrannar alltid ärver nämnaren, medan vänstergrannar ärver täljaren. Om vi följer arvet upp i trädet från våra två tal, kommer vi till slut fram till två tal, som faktiskt är omedelbara grannar, och därför är det första talets nämnare lika med andra talet täljare.

I den allra sista situationen är två tal grannar i raden, men i trädet skedde en radbrytningen mellan det första och det andra talet. Men vi ser att alla tal i slutet av raderna har nämnare 1, medan alla i början av raderna har täljare 1, så egenskapen bevaras här också.

Bråkraden har även andra egenskaper. Kan du komma på några?

Calkin Wilf-träd, Del 2

Lösningen till problemet för de yngre vecka 41

Mattegåta

Ibland blir addition av bråk någonting snyggt!

Men vad är x lika med? Skriv också hur du kom fram till svaret.

Diskussion

I en gammal papyrusrulle från år 1600 f.Kr., Rhindpapyrusen, förekommer massvis med matematiska beräkningar. Bland annat innehåller den bråkräkningar som ovan med tal på formen $\frac{2}{n}$ . Dessa beräkningar tog upp 9 sidor!

Räkningen ovan, men med x som konkret tal finns med på de sidorna. Men hur kan man lista ut vad x är utan att behöva plocka upp en gammal papyrus och kika?

Vi kan först fundera på hur bråkaddition sker med kända tal. För att addera tal med olika nämnare måste vi göra om bråken så att de har samma nämnare först. Och för att reda på minsta gemensamma nämnaren är det bra att faktorisera nämnarna (se lösningen nedan).

Lösning

Vi faktoriserar nämnarna i beräkningen för att inte behöva operera med så stora tal. Då ser vi att flera av talen innehåller faktorn 73.

$\frac{2}{73}=\frac{1}{60}+\frac{1}{73\cdot 3}+\frac{1}{73\cdot 4}+\frac{1}{x}$

Då kan vi multiplicera båda led med 73:

$2=\frac{73}{60}+\frac{1}{3}+\frac{1}{4}+\frac{73}{x}$

När vi ändå håller på kan vi multiplicera båda led med 60:

$2\cdot 60=73+\frac{60}{3}+\frac{60}{4}+\frac{73\cdot 60}{x}$

$120=73+20+15+\frac{73\cdot 60}{x}$

Vi förenklar allt förutom det hemska bråket:

$120-73-20-15=\frac{73\cdot 60}{x}$

$12=\frac{73\cdot 60}{x}$

Dags att multiplicera med x och dividera med 12:

$12\cdot x=73\cdot 60$

$x=\frac{73\cdot 60}{12}$

$x=73\cdot\frac{60}{12}=73\cdot 5=365$

Matteproblem för de yngre vecka 41

Mattegåta

Ibland blir addition av bråk någonting snyggt!

Men vad är x lika med? Skriv också hur du kom fram till svaret.

Lösningen till problemet för de äldre vecka 39

Mattegåta

På en gata finns två radhus och i varje radhus bor två djurgalna familjer. Familjerna äger katter och hundar.

Andelen katter (kvoten mellan antalet katter och totala antalet katter och hundar) hos första familjen i första huset är större än andelen katter hos första familjen i andra huset. Andelen katter hos andra familjen i första huset är större än andelen katter hos andra familjen i andra huset.

Måste det vara så att andelen katter i första huset är större än andelen katter i andra huset?

Diskussion

När frågan är formulerad på detta sättet så kan man misstänka att det är något lurt. Kanske att svaret säger emot intuitionen och det måste finnas motexempel mot att andelen katter i första huset totalt är större.

Ofta för att hitta motexempel i sådana problem är det viktigt att tro på att exemplet finns. Eller, om man ska visa motsatsen, det vill säga att det alltid måste vara så som påståendet säger, hjälper det att tro på påståendet. Man vet förstås inte om antagandet är rätt från början förrän beviset (eller exemplet) är klart. Men det hjälper rent psykiskt att tro på sin teori.

Som vi ser i lösningen nedan kan man faktiskt tänka sig fram till ett motexempel.

Mycket riktigt påpekade Erik Thörnblad för mig att det här problemet påminner om Simpsons paradox.

Simpsons paradox

I sannolikhet och statistik innebär Simpsons paradox att två olika grupper kan ha en viss tendens, men tendensen är helt omvänd när grupperna sätts ihop.

På bilden nedan syns att både den blå och den röda gruppen visar en växande trend, men på det stora hela är trenden avtagande.

Lösning (av Erik Svensson)

Låt A och B vara familjerna i Hus 1, och låt C och D vara deras grannar i Hus 2.

Låt oss anta, med avsikt att konstruera ett motexempel, att A har väldigt många fler djur än de andra familjerna och att hälften av dem plus 1 är katter. Till exempel kan vi låta A ha 5001 katter och 4999 hundar. Låt C ha 1 katt och 1 hund. Då är andelen katter hos A större än hos C.

Om B nu har relativt få djur så kommer dessa inverka väldigt lite på den totala andelen katter i huset, eftersom det stora antalet djur A har kommer dominera fullständigt. Vi låter D har väldigt få djur också, men samtidigt ha en större andel katter än A har. Exempelvis kan D ha 2 katter och 1 hund. Vi låter nu B har en större andel katter än D, låt säga 3 katter och 1 hund.

Nu har A en större andel katter än C, och B en större andel än D. Vi finner dock att i Hus 1 så är obetydligt mer än hälften av alla djur katter, men i Hus 2 har vi 4 katter och 2 hundar, och alltså är andelen katter där 2/3.

Matteproblem för de äldre vecka 39

Mattegåta

På en gata finns två radhus och i varje radhus bor två djurgalna familjer. Familjerna äger katter och hundar.

Måste det vara så att andelen katter i första huset är större än andelen katter i andra huset?

Lösningen till problemet för de yngre vecka 34

Mattegåta

Hitta två äkta bråk, det ena med nämnaren 8 och det andra med nämnaren 13, så att differensen mellan det största och det minsta av dem är så liten som möjligt.

Diskussion

Vad menas med att ett bråk är äkta? Det är ett bråk vars täljare är mindre än dess nämnare (och båda är positiva heltal). Exempel på äkta bråk är $\frac{3}{5}$ och $\frac{100}{101}$ . Ett äkta bråk har alltså alltid ett värde mellan 0 och 1!

Nu har vi ett lite fuskigt sätt att lösa problemet, de äkta bråken med nämnare 8 respekrtive 13 är ju inte så många! För att gissa svaret kan man sätta ut alla äkta bråks värden på tallinjen. Tag nämligen sträckan mellan 0 och 1 och dela in i åtta lika stora delar. På markeringarna har vi bråken $\frac{1}{8}, \frac{2}{8}, \frac{3}{8}, \frac{4}{8}, \frac{5}{8}, \frac{6}{8}$ och $\frac{7}{8}.$

Samma sak kan göras med trettondedelar, men det är lite för plottrigt att göra det på samma bild, eller hur? Det vore smidigare att rita en exakt bild, där $\frac{1}{13}, \frac{2}{13}$ och så vidare är utsatta, om sträckan hade en naturlig uppdelning i just 13 delar. Med andra ord, om antalet markeringar kan delas både med 8 och med 13, så är det ganska lätt att se skillnaden mellan bråken också.

Därför söker vi talens minsta gemensamma multipel, med andra ord det minsta positiva heltalet som både är delbart med 8 och med 13. Minsta gemensamma multipel betecknas också MGM. Och den största gemensamma delaren betecknas SGD, det behövs för att bestämma MGM av 8 och 13.

Lösning (av Toomas Liiv)

SGD(8,13)=1. Nämnarna är relativt prima.

MGM(8,13)=8*13=104, vilket också är minsta gemensamma nämnare till bråken.

Differensen av det största och minsta bråket kommer också att kunna skrivas med nämnaren 104 som ett äkta bråk. Det minsta sådana bråket är $\frac{0}{104}$ , vilket uppnås med bråken $\frac{8}{8}$ och $\frac{13}{13}$ , men dessa är olyckligtvis inte äkta bråk.