visare – Mattebloggen

En lektion för små barn om vinklar på klockan och delbarhet

Detta är en kortfattad planering av en del av en lektion med barn på 5, 6, 7 respektive 10 år. Där det inte står något är aktiviteterna riktade åt de yngre barnen.

Notera att barnen redan har haft en introduktion till vinklar och olika vinkeltyper.

Klockan

Vinklar på klockan

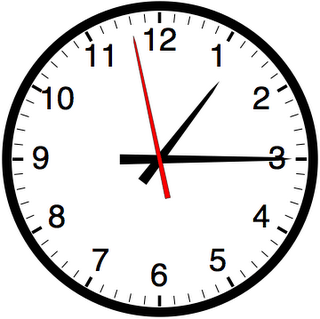
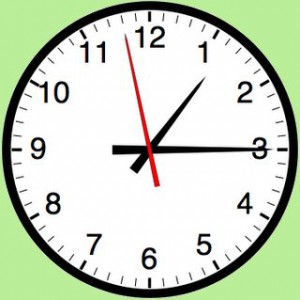
Var hittar vi vinklar i rummet? Det är svårt att hitta spetsiga och trubbiga vinklar, men klockans visare bildar oftast en spetsig eller trubbig vinkel. Vi tar fram en modell av en klocka med två visare och snurrar ena visaren. Barnen säger under tiden vilken vinkel det är mellan visarna (”trubbig, trubbig, trubbig, trubbig, RÄT, spetsig, spetsig, spetsig, jättespetsig…”).

Vad är klockan om visarna bildar en rät vinkel (om minutvisaren är på tolv)? De yngre barnen får experimentera med en klockmodell, medan de äldre får föreställa själva. Hur ofta sammanfaller visarna, kan man fråga de äldre barnen.

Branta backar

Ställer man en spetsig vinkelns ena ben på marken blir det en backe. Vilken backe åker man snabbast nedför? Vilken backe är jobbigast att klättra upp på?

Vika papper

Tänk om vi har varken linjal, gradskiva eller sax med oss! Det enda vi har är ett papper. Hur kan vi få fram en rät vinkel? Vad ska vi göra om pappersbiten är rund och inte triangulär från början?

De äldre barnen får i uppgift att vika ihop vinklar på 180, 90, 45 samt 60 grader.

Färga klockans siffror

Vi ska göra den tråkiga klockan lite snygg och färglägga cirklarna med siffror. Går det att måla cirklarna i två färger, så att varannan cirkel har en färg? Kommer det att gå ihop på slutet? Går det med 3 färger? 4 färger? 5 färger?

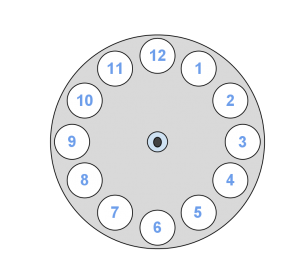
Tio- och kanske sjuåringarna får hitta tal upp till 100 som går att färga i både 2,3,4,5 och 6-färgsmönster.
I samband med det får de kort där de snabbt ska gissa hur många cirklar det finns av en viss färg.

Till exempel, hur många röda cirklar är det på bilden? Svara utan att räkna dem en efter en!

Bygga ihop $360^\circ$

Vi fortsätter på uppgiften från förra gången. Nu gäller det att inte bygga en cirkel utav vilka bitar som helst, utan av exakt två typer av bitar. Det finns inte så många lösningar till den här uppgiften om man lägger på begränsningar på att varannan bit ska ha samma färg (ett exempel är $90^\circ+30^\circ+90^\circ+30^\circ+90^\circ+30^\circ$ ). De äldre barnen får försöka bevisa att de har hittat alla lösningar.

Lösningen till problemet för de yngre vecka 46

Mattegåta

När Dag tog studenten, fick han en klocka som hade en timvisare, en minutvisare och en sekundvisare. Hur många gånger per dygn sammanfaller alla tre visarna? (Förklara varför.)

Diskussion

Det här var ett svårt problem. Ett förvirrande faktum är vi måste studera tiden i dubbel bemärkelse. Problemet hade egentligen varit densamma ifall tre löpare hade sprungit med olika hastigheter runt en bana. Vi undrar när alla tre träffas, så vi kommer betrakta visarna som löpare.

Hur snabba är de då? Sekundvisaren är snabbast och ”springer” med hastigheten ett steg per sekund (stegen är de 60 markeringarna på klockan). Sedan kommer minutvisaren som tar en sextiondedels steg per sekund och långsammast är timvisaren, som ”promenerar” med hastigheten 1/720 steg per sekund (5 steg per timme eller 60 steg på 12 timmar). Nu kan vi pilla med hastigheterna om vi vill för att se när de olika visarna träffar varandra.

Lösning

Vi kan börja med att undersöka när två av visarna, minutvisaren och timvisaren, träffar på varandra under ett dygn. De börjar klockan 0:00 på samma ställe, på tolvan, och sedan rycker minutvisaren iväg. Eftersom minutvisaren klarar av 60 steg på en timme, medan timvisaren tar 5 steg, kommer de att träffas nästa gång efter mer än 1 timme. Mer exakt tar det faktiskt 12/11 av en timme. Minutvisaren drar iväg sedan och kommer gå om timvisare med jämna mellanrum.

Så minut- och timvisaren träffas:
1. efter 0 timmar (de börjar på samma ställe)
2. efter 1 och 1/11 timme
3. efter 2 och 2/11 timme
4. efter 3 och 3/11 timme
5. efter 4 och 4/11 timme
6. efter 5 och 5/11 timme
7. efter 6 och 6/11 timme
8. efter 7 och 7/11 timme
9. efter 8 och 8/11 timme
10. efter 9 och 9/11 timme
11. efter 10 och 10/11 timme
12. efter 11 och 11/11 timme = 12 timmar
13. efter 13 och 1/11 timme
14. efter 14 och 2/11 timme
15. efter 15 och 3/11 timme
16. efter 16 och 4/11 timme
17. efter 17 och 5/11 timme
18. efter 18 och 6/11 timme
19. efter 19 och 7/11 timme
20. efter 20 och 8/11 timme
21. efter 21 och 9/11 timme
22. efter 22 och 10/11 timme
23. efter 23 och 11/11 timme = 24 timmar, vilket är ett nytt dygn, så det räknas inte!

Så minutvisaren och timvisaren träffas 22 gånger per dygn, men vilka av gångerna hakar sekundvisaren på?

Vi kan kolla på vilka positioner sekundvisaren hamnar efter perioder på 1 och 1/11 timme. Sekundvisaren har hastigheten 3600 steg per timme, så totalt kommer den gå en massa varv plus 3600/11 steg som är lika med 327 och 3/11 steg som är lika med 5 varv och 27 och 3/11 steg. Så på klockan kommer visaren att hamna mellan femman och sexan nånstans. Vi kollar alla situationer då timvisaren sammanföll med minutvisaren:

1. sekundvisaren är på 0 steg = prick på klockan 12!
2. sekundvisaren är på 27 och 3/11 steg = mellan kl 5 och kl 6
3. sekundvisaren är på 54 och 6/11 steg = mellan kl 10 och kl 11
4. sekundvisaren är på 21 och 9/11 steg = mellan kl 4 och kl 5
5. sekundvisaren är på 49 och 1/11 steg = mellan kl 9 och kl 10
6. sekundvisaren är på 16 och 4/11 steg = mellan kl 3 och kl 4
7. sekundvisaren är på 43 och 7/11 steg = mellan kl 8 och kl 9
8. sekundvisaren är på 10 och 10/11 steg = mellan kl 2 och kl 3
9. sekundvisaren är på 38 och 2/11 steg = mellan kl 7 och kl 8
10. sekundvisaren är på 5 och 5/11 steg = mellan kl 1 och kl 2
11. sekundvisaren är på 32 och 8/11 steg = mellan kl 6 och kl 7
12. sekundvisaren är på 59 och 11/11 steg = 60 steg = 0 steg = prick på klockan 12!
Sedan upprepar historien sig!

Ingenstans, förutom klockan 12 på natten och på dagen hamnar sekundvisaren ens mellan rätt siffror (t.ex. i situation 8 är sekundvisaren mellan kl 2 och kl 3, medan minut- och timvisaren är mellan kl 7 och kl 8). Detta betyder att alla tre visarna träffas exakt två gånger per dygn!

Matteproblem för de yngre vecka 46

Mattegåta

När Dag tog studenten, fick han en klocka som hade en timvisare, en minutvisare och en sekundvisare. Hur många gånger per dygn sammanfaller alla tre visarna? (Förklara varför.)