Problemlösning – Sida 2

Tredje träffen med Matteklubben, åk 2-4

Minsta eleverna som går i Matteklubben är de i åk 2-4. Du kan också läsa om den första träffen och den andra träffen med gruppen.

Från början hade vi tänkt att både ha med en del med blandade problem och en tematisk del. Vi hann dock bara gå igenom blandade problemen. Dock gjorde vi det ordentligt och dessutom fanns det trots allt en röd tråd i de här problemen, även om den inte var uppenbar. Men mer om det senare!

Precis som förra gången var 29 barn och 6 lärare med på träffen.

En lek med frågor

För att barnen skulle lära känna varandra i gruppen (och inte bara känna dem från egna skolan) började vi lektionen med en frågelek. Egentligen är det en matematisk lek, men det är inte helt uppenbart varför.

Reglerna var enkla: jag eller någon annan lärare tänkte på en person i klassrummet. Eleverna skulle ställa ”ja/nej”-frågor till oss för att ta reda på vem det var. Den som räckte upp handen fick chansen att ställa nästa fråga och jag försökte hela tiden välja personer som inte hade ställt någon fråga tidigare.

Men hjälp av frågorna ”Är det en tjej eller en kille?” (varpå jag svarade ”Ja” och frågan ändrades till ”Är den en kille?”), ”Är det jag?”, ”Är det han?”, ”Sitter personen på mittenraden?”, ”Har personen en blå tröja?” etc. kunde barnen gissa rätt person på 11 försök.

Lek i grupper

Nu skulle barnen testa samma lek i grupper om 4-6. Vi gav ut papper för att de skulle anteckna antalet frågor det tog att gissa personen som någon i gruppen tänkte på. På tavlan skrev jag upp gruppernas rekord: ”5 försök, 7 försök, 1 försök(!)…” Möjligen blev fokusen vid att ha så få försök som möjligt för stor, vilket gjorde att barnen ofta chansade just för att kunna gissa personen på ett försök. I snitt blev barnen bättre på att spela spelet, då oftast tog det mycket mindre än 11 försök.

Efter ett en stund pratade vi om vilka frågor som var bra att ställa. Egentligen syftade jag på frågor som ungefär halverar gruppen av misstänkta personer. Men jag formulerade inte, då barnen ändå förstod det intuitivt efter att ha lekt med frågorna.

”Är det en kille?”, ”Är det ett barn?”, ”Sitter personen på mittenraden?”, ”Har personen en långärmad tröja?”, ”Har personen ljust hår?” var några av de riktigt bra exempelfrågor som barnen kom på.

Blandade problem, del 1

Därefter delade vi ut ett blad med fem blandade problem. Det visade sig att problemen absolut inte var för lätta. Alla hade något att klura på, så jag ville inte skynda på processen bara för att hinna med en del till. Istället gjorde vi uppehåll i lösandet, då vi gick igenom de första två problemen och sedan tog vi rast.

Eleverna försöker alltid lösa problemen i ordning och hoppar oftast inte över något problem förrän de känner sig klara eller uttråkade. Nästan alltid har de några idéer på varje uppgift de hunnit börja på, så det finns alltid något att diskutera med varje grupp.

1. a) Hur många tvåsiffriga tal finns det?
b) Hur många tresiffriga tal finns det?

Elever: På a) är svaret 90
Lärare: Hur tänker ni?
Elever: Det är 99 tal som har upp till två siffror, men 1,2,3,4,5,6,7,8,9 är inte tvåsiffriga, dem måste vi ta bort.
Lärare: Japp, och var blir svaret på b)?
Elever: 990 eller.. 989… eller…
Lärare: Försök att räkna på liknande sätt. Hur många tal har upp till tre siffror och hur många måste vi räkna bort?

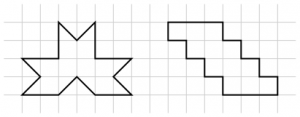
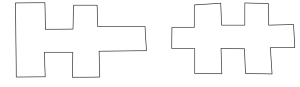
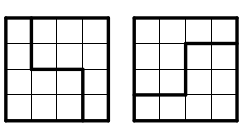
2. Skär ett 4×4-rutnät i två identiska delar. Försök att finna flera olika sätt. Nedan ser du två sätt, som egentligen är ett och samma:

samma_satt

Elever: Räknas de här (pekar på olika sätt)?
Lärare: Ja, de här är olika, men dessa (pekar på två egentligen likadana sätt) räknas som samma, eftersom man kan vrida bilden så att det ser likadant ut.

I vissa fall tyckte alltså eleverna att alla fyra sätten som här på bilden räknades som samma, i andra fall ansågs det att de räknades som två olika sätt (vänsterbilderna som ett sätt, högerbilderna som ett annat, eftersom de inte gick att vrida om till varandra).

uppdelningar_upprepning

Redovisning, del 1

Några elever fick komma fram och redovisa uppgift 1 (en grupp fick punkt a), den andra punkt b) då vi alltid har många frivilliga som vill fram, så jag försöker att ha framme så många olika personer som möjligt under lektionen).

På punkt b) fanns flera olika sätt att tänka, och gruppen vid tavlan gjorde en väldigt snygg lösning. De tog 1000 tal (1 till 1000), och sedan tog bort 100 (vad jag minnst). Det blir 900. Men 100 ska egentligen räknas med så det blir +1, det vill säga 901. Men 100 ska inte räknas med så det blir -1, det vill säga 900.

På andra uppgiften fick många grupper komma fram (en grupp i taget) och rita upp ett av sina sätt. Det blev totalt omkring 8 sätt, bland annat de här:

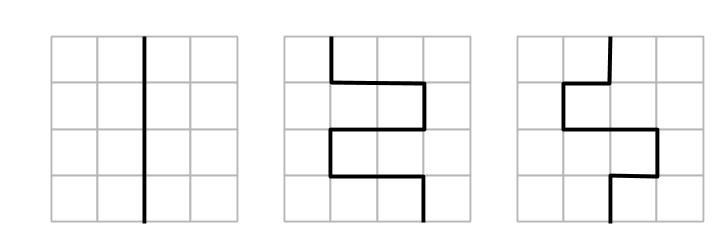
uppdelningar

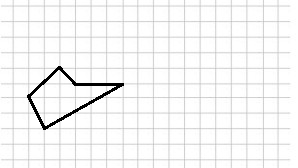
Några av eleverna begränsades inte av tänket ”måste skära längs med rutorna” och gjorde på följande sätt:

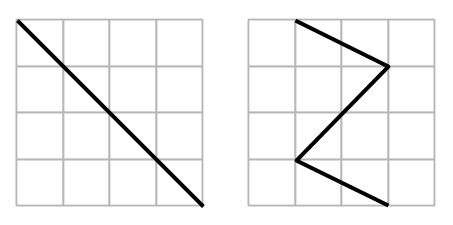
uppdelningar_kreativa

Det stod ju trots allt inte i uppgiften att man var tvungen att skära längs med rutorna (för mig var det underförstått). Det kom lite upprörda röster från vissa som tyckte att det inte räknades, och jag försökte säga att det egentligen blev två olika problem som vi löste. Och att dessa kreativa lösningarna räknades när man löste den ena versionen av problemet, men inte den andra.

(Lärdomen är att vara tydligare i uppgiftsformuleringen.)

Jag visade även att man kunde få alla uppdelningar genom att rita en linje som var symmetrisk kring centrum (eller snarare, några barn greppade vad jag var ute efter när jag frågade om uppdelningslinjen betedde sig på något speciellt sätt). Detta kan man säga även om linjer som inte följer rutgränserna.

Blandade problem, del 2

3. Ett litet barn har 3 röda och 2 blå kuber. Alla kuberna har samma storlek. Hur många 5 kuber höga olika torn kan barnet bygga?

Elev: Det finns ju jättemånga sätt! Jag vet inte om orkar rita upp alla.
Lärare: Försökt att göra det på ett strukturerat sätt. Då är det lättare att få översikt och inte glömma bort något sätt.

4. Det finns 60 trästockar, som alla är 3 meter långa, som ska huggas upp i halvmeterlånga delar. Hur många sågningar måste man göra?

Elev: Det är 6 bitar som varje stock delas upp i, således blir det 60*6 = 360 sågningar.
Lärare: Men är det verkligen 6 sågningar per bit? Hur många gånger skulle vi såga för att dela upp en stock i två bitar?
Elever: En..
Lärare: Och i tre bitar?
Elever: Två..
Lärare: Och i fler bitar?
Elever: Aha… (och man ser en aha-upplevelse i deras ansikten), det behövs 5 sågningar per stock, så svaret blir 60*5.

5. En bit föll ur en gammal tidskrift.
Första sidan hade numret 328 och sista hade ett nummer som bestod av samma siffror, men i en annan ordning. Hur många sidor föll ut ur tidskriften?

magazine

Elever: Sista sidan måste vara udda, alltså är det 823.
Lärare: Varför inte 283 då?
Elever: Men det är ju mindre, det ska vara större! Och då är det 823 – 328 = 495 sidor som ramlade ur.

Här blev det långa diskussioner med många av grupperna om vad som är sidor, vad som är blad (två sidor), om svaret verkligen kunde bli ett udda antal sidor och hur man egentligen ska räkna antalet sidor i en bit. Många hade svårt att förstå att man skulle (och varför man skulle) lägga till 1 efter subtraktionen.

Ladda ner uppgifterna för utskrift

Redovisning, del 2

Här hade vi inte så mycket tid kvar, så redovisningen gick ganska snabbt.

För att lättare föreställa sig tornet från uppgift 3 ritade jag upp det:
undervisar

Sedan frågade jag vilket svar alla hade fått och skrev upp förslagen som sades högt: 20, 10, 11. Grupperna fick förklara från sina egna platser hur de fick just det svaret.

Den tydligaste strategin hade gruppen som hade svaret 10 (vilket också var rätt svar): Att först räkna de 4 fallen då en av de blåa kuber är längst ner. Sedan är det 3 fall kvar när en är näst längst ner (nu är det en röd längst ner, eftersom vi redan har betraktat de andra möjligheterna). Fortsätter man så, får man till slut svaret 4 + 3 + 2 + 1 = 10.

Lustigt nog blev inte alla barnen övertygade om svaret, utan en elev envisades med att svaret var 11 (eleven skrev upp alla möjligheter). Vi lärare föreslog att det antagligen fanns två sätt som sammanföll, men eleven stod på sig. Tyvärr hann vi inte kolla på dessa sätt efter lektionen. Men det är imponerande med sådant matematiskt självförtroende! Den finns i mycket mindre grad hos äldre elever.

På uppgiften om stockar fick en elev gå fram till tavlan och redovisa. Men det blev ett tankefel med antalet skärningar per stock, vilket eleven fick till 3. Tillsammans hjälpte klassen till att korrigera antalet sågningar per stock till 5, vilket till slut gav rätt svar.

Två elever kom fram och redovisade uppgiften om sidorna. De motiverade bra och räknade skillnaden rätt, men de behövde också förklara varför det inte bara är skillnaden, utan skillnaden plus ett som ger det rätta antalet sidor. Eleverna förklarade det med att man ”lägger tillbaka” sidan nummer 328.

Vi var tvungna att avbryta på grund av tiden, men jag tror att några hann förstå att det inte är så enkelt som att bara räkna ut skillnaden mellan två tal, när man ska ta reda på hur många tal det är som ligger mellan dem.

Röd tråd genom blandade uppgifter

Det gemensamma tankesättet för uppgifterna 1, 4 och 5 blev just ”effekten +/-1”, som går ut på att man får ett fel svar eller delsvar, som avviker med 1 från det korrekta. Effekten är ett mycket vanligt tankefel som händer de flesta vuxna och dyker också ofta upp i programmering. När man inte stannar upp och tänker efter så kan man tro att det måste ske 6 sågningar för att dela upp ett stock i 6 delar, men det ska vara 5.

En ännu mer generell idé som används vid lösningen av dessa uppgifter är att ha koll på vad man lägger till och vad man tar bort. Till exempel, i uppgift 1 b) kan man lägga till talen 1 till 999, och sedan ta bort talen 1 till 99. Då är det lättare att se att svaret är 999 – 99 = 900. I uppgiften om sidor kan man först räkna med alla sidor från 1 till 823 (823 stycken) och sedan ta bort 1 till 327 (eftersom 328 ska finnas med) och då få 823 – 327 = 496 sidor.

Den andra idén hade svårare att få fäste hos eleverna, möjligen behöver de öva mer på den i framtiden (medelst något lättare uppgifter, som t.ex. nummer 1). Det var också svårare att greppa tankesättet när de jobbade med så pass stora tal som 823 och 328. De hade ingen intuitiv känsla för talen, och sade ofta att skillnaden de emellan var 505 (800 – 300 = 500, 28 – 23 = 5). Jag ska nog vara försiktig med att använda stora tal i uppgifter som går ut på att upptäcka nya idéer.

Känslan efter lektionen

Trots att vi inte hann med temat, kändes lektionen fullständig. Det blev lite variation i och med leken i början av lektionen, vilken kändes uppskattad av eleverna. Trots att vi var lika många som förra gången, så kändes det mycket lugnare än vanligt, kanske för att alla var vana vid arbetssättet vid det här laget.

Bland det bästa med eleverna i åk 2-4 är att de inte håller sig för att säga sanningen. De kan både öppet kritisera och säga lovord. Denna gång blev jag väldigt glad när en av eleverna sade att Matteklubben-dagar var tillsammans med födelsedagen hennes favoritdagar! Sånt blir man glad av att höra och jag hoppas att flera elever känner något liknande.

Jag ser fram emot nästa träff, den sista före Jul, då vi också kommer att ha en liten utvärdering om höstterminen.

Tredje hemuppgiften från Matteklubben, åk 5-6

Här i kommentarerna kan du diskutera hemuppgiften. Skriv om du har frågor eller förslag på lösning/svar.

• I ett höghus med 100 våningar finns en hiss, som bara har två knappar: ”+7” och ”-9”. Den första knappen får hissen att gå upp sju våningar, den andra får den att flytta sig 9 våningar ner. Går det att åka från vilken våning som helst till vilken annan våning som helst?

• Hästar står på ett litet schackbräde så som det syns på den vänstra bilden. Hästarna följer schackreglerna när de gör drag. Kan de efter några drag ställa sig så som den högra bilden visar?

horses

Tredje träffen med Matteklubben, åk 5-6

Matteklubben är Uppsala kommuns satsning på begåvade elever i matematik. Jag har äran att förbereda aktiviteterna som vi håller på med och vara en av lärarna. Du kan kolla upp var vi gjorde på första träffen och andra träffen innan du läser vidare.

Många lärare

Till Matteklubbens träffar kommer cirka 30 elever och antalet lärare brukar bli ungefär en på 5 elever. Några frågar mig vad alla lärare utom mig gör och jag brukar svara att de verkligen behövs! Det finns alltid saker att göra: Allt från att dela ut pennor och fika till att delta i matematiska diskussioner med de mest envisa eleverna. Det är väldigt bra att vara fler än en lärare, är man ensam så kan man göra något grovt matematiskt fel och det är inte säkert att någon upptäcker det. Det gör ingenting om en lärare har fel, men det är viktigt att reda ut felen. Eleverna måste se att det är sanningen i matematiken som gäller, och inte lärarnas subjektiva (och möjligen något auktoritära) åsikter.

Hemuppgiften

Lektionen började med läxan, precis som förra gången. Den hade ingen gjort så det blev en klassdiskussion.

Först undersökte vi vad som hände med en figur vars sidor blir hälften så stora. Hur många gånger mindre blir arean? En elev förklarade att om man tänkte på en kvadrat, så såg man att den gick från att vara fyra rutor till att bara vara en. Därmed kunde man se att arean blev fyra gånger så liten.

Den andra uppgiften var (är och förblir) riktigt svår, så jag ställde en ledande fråga till klassen. Det var en uppgift vi hade förra gången, om hur man kan rita en kvadrat med dubbel så stor area som en given. Det vill säga, rita en kvadrat på ett rutat papper med arean lika med exakt två rutor.

Många elever föreslog att man skulle förstora varje sida 1,5 gånger. En elev hade kollat upp med sin pappa att sidan i målkvadraten är roten ur 2, det vill säga ungefär 1,4. Båda förslagen vände jag mig emot med argumentet att det då inte blir en exakt bild (och arean blir inte heller exakt 2). Och om sidorna förstoras 1,5 gånger visade min kollega på tavlan att arean faktiskt blir större än 2. Det visade sig i diskussionen med kollegan senare att de gamla grekerna tänkte på precis samma felaktiga sätt som barnen på Matteklubben, de ville också förstora sidorna med 1,5.

Jag gav ledtråden om att en ruta består av två trianglar. Hur kan man rita en figur som består av dubbelt så många trianglar? En eller två av eleverna kunde då rita en korrekt bild på tavlan, det vill säga en vriden kvadrat, där sidorna utgörs av rutdiagonaler. Jag poängterade att denna figur har exakt dubbelt så stor area som en ruta.

För att lösa läxans andra uppgift tipsade jag om att kombinera svaren på uppgifterna vi har diskuterat hittills. Man ska egentligen tänka på samma sätt som i problemet där en kvadrat ska få dubbelt så stor area.

Grafteori

När man är nybörjade på matematisk problemlösning, vet man inte alltid hur uppgifter kan börja lösas. Det gäller då att visa upp många olika verktyg för barnen, för att de ska kunna välja det som passar vid varje tillfälle. Tillsammans med eleverna skapar vi en schweizisk armékniv med problemlösningstekniker. Men det är viktigt att inte behöva övertala dem (vilket ofta sker på vanliga mattelektioner) om att en viss teknik är viktig och kommer troligen att användas ”senare”. Istället väljer jag uppgifter där en viss teknik uppstår naturligt, och man ser direkt hur det underlättar problemlösandet.

En sådan teknik går utt på att rita scheman över objekt som finns i problemet, det som på högnivå-mattespråk kallas ”att rita en graf”.

Uppgifterna

Vi hade bara tre uppgifter på temat, men det var ganska mastiga alla tre. Många hann lösa ettan och börja på tvåan, men trean hann jag knappt diskutera med någon grupp.

Under uppgifterna står vanliga dialoger som skedde på lektionen.

1. I vår solsystem finns 8 planeter och Pluto, som en gång i tiden räknades som planet. Man utvecklade rymdturismen genom att erbjuda följande rutter (både fram och tillbaka): Jorden-Merkurius, Pluto-Venus, Jorden-Pluto, Pluto-Merkurius, Merkurius-Venus, Uranus-Neptunus, Neptunus-Saturnus, Saturnus-Jupiter, Jupiter-Mars, Jupiter-Neptunus, Mars-Uranus.

(a) Går att ta sig från Jorden till Mars?

Vissa elever missade ”fram och tillbaka” och vissa var lite osäkra på vilka planeter man fick åka emellan (det vill säga om man fick ”mellanlanda”). När vi redde ut dessa saker kunde de fortsätta med problemet.

Elever: Svaret är ”ja”….eller ”nej”… kanske… vi vet inte riktigt.
Lärare: Om det går, hur skulle man gå tillväga då? Hur skulle man exakt åka, mellan vilka planeter?

Elever: Svaret är ”nej”, för om man tar sig till Mars måste man komma från Uranus eller Jupiter, och om man ska ta sig till Jupiter så är det från Saturnus eller Neptunus, och till Neptunus kommer man från Jupiter så det går inte.
Lärare: Men ni har inte missat några utvägar då? Har vi verkligen kollat alla möjligheter? För att vara säkra så kan ni rita ett schema lite som scheman nedan.

(b) Vilka av scheman nedan kan representera ruttsystemet?

Uppgifterna (b) och (c) diskuterade jag med hela klassen ståendes framme vid tavlan. Några elever fick komma fram och rita egna scheman, samt säga vilka av scheman på bilden som fungerade för uppgiften. Eleverna kunde även korrekt förklara att man kunde bestämma Saturnus, men inga andra planeter. Rättare sagt, tillsammans kunde de exakt bestämma vilka villkor gällde för Saturnus (kopplad till två planeter, som båda är kopplade till tre planeter). Många kunde även förklara varför det inte gick att bestämma andra planeter med säkerhet.

2. Några barn i klassen kan spela olika musikinstrument: Pia kan spela gitarr och piano, Ville kan spela gitarr och dragspel, Tommy – fiol och cello, Daniel – bas och trumpet, Lena – piano och dragspel, Sara – fiol och trumpet, Solveig – cello och bas. På hur många sätt kan man ge var och en av dem ett instrument (alla instrument måste vara olika) så att alla kan spela samtidigt?

Elever: Vi ritade ett schema och såg att varje barn var kopplad till två instrument och varje instrument spelas av två barn.
Lärare: Kan man rita schemat på något annat sätt så att det ska bli lättare att bestämma svaret i uppgiften?

Elever: Vi gjorde en tabell och skrev upp alla möjligheter. Det blev fyra.
Lärare: Är ni säkra på att ni inte missade några möjligheter?

Även denna uppgift gick jag igenom på tavlan för att visa exempel på hur man ”snyggar till” scheman. Tricket är att inte bara rada upp instrumenten på ena raden och barnen på andra raden och sedan börja koppla ihop dem. Istället kan man börja med ”gitarr-Pia-piano” och sedan fortsätta med nästa person som ska spela piano och vidare göra så tills cirkeln är sluten. Då får man ett mycket tydligare schema. Jag visade att det då var självklart att ena cirkeln kunde fördela instrumenten på två sätt och andra också på två.

Vad blev svaret då? ”Fyra”, svarade barnen. ”Två plus två eller två gånger två?” undrade jag. Många av barnen förstod inte riktigt hur jag menade (”Det är ju samma sak!”). Men när jag förklarade att om det hade varit 2 och 3 sätt i respektive cirkel, skulle jag då addera eller multiplicera dem, så förstod många att det var multiplikation jag var ute efter. Kul att visa att 2+2 och 2*2 inte ”betyder” samma sak. Återigen, att det är hur man tänker, och inte svaret, som räknas.

3. I ett höghus med 100 våningar finns en hiss, som bara har två knappar: ”+7” och ”-9”. Den första knappen får hissen att gå upp sju våningar, den andra får den att flytta sig 9 våningar ner. Går det att åka:
(a) Från första våningen till den andra?
(b) Från den andra våningen till den första?

En del elever hann nosa in på den här uppgiften och lösa (a) och möjligen (b) också. De som var klara fick kika på hemuppgifterna, där de ofta fortsatte med hissuppgiften. Se nästa inlägg för fler detaljer.

Ladda ner för utskrift

Regatta

Andra delen av lektionen genomförde vi en liten tävling, matteregatta. Regattan var planerad i tre omgångar, men vi hann bara med två, och dessutom fick vi korta ner den andra omgången till 10 minuter.

Elevernas delade sig själva upp i par och sedan sattes paren ihop till lag om fyra. Vissa lag fick vara tre personer. Alla lag fick heta någon frukt som till exempel lag Ananas (för att inte slösa bort tid på att hitta på lagnamn gav jag alltså ut lagnamnen). Sedan fick de för första gången öva på att skriva ner lösningar på Matteklubben (och inte bara berätta dem). Juryn, vilket var de andra lärarna, satte poäng på lösningar som de hade fått in.

Efter att eleverna var klara med första omgången, gick jag igenom lösningarna, medan juryn rättade. Därför kan jag inte säkert säga varför poängen blev som det blev, annat än att juryn bedömde fullständighet och korrekthet. När omgången var rättad, fick alla höra poängen samtidigt som att de fick möjligheten att protestera över sin poäng. Då är tanken att juryn går igenom lösningen en gång till och kollar efter om lösningen eventuellt är värd mer poäng.

Tanken med den demokratiska aspekten är återigen att minska auktoritetens betydelse och ta bort eventuell objektiv bedömning från matematiken. Det är som till slut är värt poäng är resonemanget som finns nedskrivet på pappret, och inför det står alla lagen lika.

Vi fick dra över tiden lite grann för att på samma sätt hinna gå igenom andra omgången. Om du är intresserad av riktlinjerna som juryn hade vid rättningen, så kan du ladda ner dem här nedan.

Ladda ner uppgifterna för utskrift

Ladda ner lösningarna och rättningskriterierna för utskrift

Resultat

Här är regattans fullständiga slutgiltiga resultat. Grattis återigen till lag Mango som vann i en jämn kamp!

Tankar efter lektionen

Efter lektionen samlades vi alla lektionsledarna för att diskutera vad som har gått bra och dåligt. Vi var som vanligt imponerade av elevernas förmåga att ta åt sig nya idéer. Det kändes också att lektionens uppgifter blev bra (lagom svåra och roliga).

Det som man hade kunnat göra bättre var att ha ett tydligare schema, som eleverna och lärarna skulle försöka hålla sig till. Det hade varit bra bland annat för att hinna med den inplanerade tävlingen. Lektionen kändes också något stökigare än vanligt och där skulle fasta tider ha hjälpt. Det var bra med rast tyckte alla lärare!

Det ska bli spännande att träffa eleverna en sista gång innan Jullovet. Då blir det också dags för utvärdering!

Andra hemuppgiften från Matteklubben, åk 7-9

På lektionen bevisade vi att vinkelsumman i en godtycklig triangel är 180° och en i fyrhörning 360°. Hur blir det med en femhörning, sexhörning osv.? Och hur bevisar man resultatet?

Det är inte bara månghörningar som har en viss bestämd vinkelsumma, utan andra figurer också. Vad blir vinkelsumman i en stjärna och varför är det alltid så?

Det här är alltså uppgifterna man kan tänka på hemma inför nästa Matteklubben-möte:

• Bestäm vinkelsumman i en n-hörning.

• Bestäm vinkelsumman (av de markerade vinklarna) i en femuddig stjärna.

stjarna

Andra träffen med Matteklubben, åk 7-9

Under andra matteträffen med högstadiet hade vi 19 elever som besökte oss. Vi var 3 lärare plus en till som hjälpte lite grann. Det var alldeles lagom för en grupp med elever som inte så ofta räcker upp handen. Men hade eleverna varit lika aktiva som de i åk 2-4, så hade vi lärare inte räckt till. Men som sagt, det var mycket lugnt i klassrummet.

Det är inte så lätt att börja med matematisk problemlösning sent i högstadiet, då man redan har lärt sig en del metoder och hur man brukar göra i matten. Det finns många uppfattningar om hur man bör göra som vi på Matteklubben försöker ändra lite. Det vill säga, vi vill visa dels att man kan göra matte på många olika sätt, dels vill vi lära ut att vara rigorösa i ens tänkande (annars blir det något annat än matte). Det är extra svårt att lära ut något när man ses så sällan!

Det var därför mycket klurigt att välja tema till lektionerna som är lagom svår, men som också är rätt ny för eleverna, där de inte redan har bestämda sätt att göra uppgifterna på. I andra länder är det vanligt att elever stöter på matematisk stringens först när de läser geometri. Samtidigt har vi i Sverige en mattetävling där eleverna presterar sämst just på geometriuppgifterna (mest för att de inte övat på sådana förut). Därför valde jag ”Vinklar” som tema på dagens lektion.

Men jag vill skriva om lektionen som har varit i kronologisk ordning, därför börjar vi med hemuppgiften.

Hemfrågan

Sist i uppgiftsbladet förra gången stod hemuppgiften. Den gick ut på att, med hjälp av att betrakta rester som tiopotenser ger vid division med talet 11, lista ut en delbarhetsprincip för talet 11.

Det var ungefär 3-4 elever som hade tänkt på uppgiften hemma, vilket är glädjande, det betyder att de tyckte att det var tillräckligt intressant och en lagom utmaning. Självklart förväntar jag mig inte att man ska titta på hemuppgiften, då det finns så mycket annat som kallar på ens uppmärksamhet. Men de som tycker att det är kul att utforska ska givetvis göra det, jag försöker att välja lagom uppgifter för det.

Innan vi tog oss an delbarhetsprincipen med 11 och elevernas teorier, repeterade vi beviset för hur man visar att ett tal och dess siffersumma ger samma rest vid division med 9. Mycket för att påminna om hur rester fungerar (att man kan subtrahera tal som är delbara med 9 och få samma rest) men också för att de som var nya på träffen skulle komma in i vad vi höll på med. Jag gjorde en tydligare uppställning än förra gången, då beviset lite hastigt gicks igenom på slutet av lektionen.

Sedan svarade vi på frågorna om vad det blir för rest när man dividerar 100…00 (jämnt antal nollor) med 11 och när man dividerar 100..00 (udda antal nollor) med 11.

I det första fallet tyckte eleverna att svaret var 1, och för att visa det subtraherade vi talet 99..99. Vi diskuterade dels hur många nior det fanns i talet (lika många som nollorna i tiopotensen), dels vad resultatet av divisionen 99..99/11 blir. Eleverna hade inte helt lätt för att svara på den frågan, förmodligen för att de inte är vana vid att jobba med icke-konkreta (stora) tal. Först fick vi svaret 99..9 (en nia mindre), men efter lite rimlighetskontroll förstod de att vi inte hade räknat rätt. En elev formulerade att svaret faktiskt blev 909090..09 (hälften så många nior). Sedan nämnde jag att det ändå inte var så jätteviktigt vad resultatet blev (men att resultatet är ett heltal är en försäkring om att talet verkligen är delbart med 11).

I det andra fallet tyckte vissa elever att svaret fortfarande var 1, men snabbt insåg vi att svaret var 10 (subtraherade talet 999…90 på samma sätt). Hur skulle vi nu kontrollera delbarheten av ett godtyckligt tal med 11?

Likt fallet med delbarhet med 9 gjorde vi ett konkret exempel med ett tal som bestod av några 10000-tal, 1000-tal, 100-tal, tiotal och ental (t.ex. 30000 + 7000 + 400 + 20 + 1). Varannan siffra gav alltså sig själv i rest (3, 4, 1) och varannan gav sig själv gånger tio (70, 20). Vi har förstås en delbarhetsprincip nu (det är bara att räkna ut summan 3 + 70 + 4 + 20 + 1 och se om resultatet är delbart med 11), men den är ju inte särskilt smidigt.

Skulle vi kunna subtrahera något mer, t.ex. från 70? från 20? Vi vill subtrahera något som är delbart med 11 för att inte förändra resten. En elev föreslog talet 66, och vi provade det och fick 4 som svar. Men det är inte självklart hur man från början skulle få den där fyran från siffran sju. På en förfrågning efter andra förslag sade en elev att man kunde subtrahera 77, och då skulle vi få -7 i summan. En annan elev insåg att det var logiskt att ta bort 22 från 20 (och då få -2 i summan). Tillsamman kom vi fram till att resultatet av 3 – 7 + 4 – 2 + 1 skulle ge ett tal med den sökta resten.

Nu bad jag en elev att formulera delbarhetsprincipen med 11, vilket blev att man räknar ut ”varannan siffra plus och varannan minus”. Vi testade slutsatsen på några exempel. På frågan om man skulle börja räkna med minus eller plus nämnde jag att det inte spelade någon roll. Det är inte trivialt varför det spelar någon roll, men jag gav en snabb förklaring om att resultatet blir precis samma, fast med omvänt tecken. Det spelar alltså roll för den exakta resten, men kvittar om vi bara ska bestämma huruvida ett tal är delbart med 11 eller inte.

Det var roligt att tillsammans bevisa den här riktigt svåra delbarhetsprincipen och se att många hängde med. Frågan är om eleverna kan upprepa det på egen hand, när de till exempel förklarar det för någon annan.

Vinklar

Jag valde vinklar som ett avsnitt i geometri, dels för att eleverna redan har mött dem och vet vad det är för något och dels för att många problem i tävlingen HMT handlar om vinklar. Lär man sig tekniken ”vinkeljakt”, det vill säga har vanan att räkna ut vinklar i olika figurer, så kan man komma ganska långt bara på det.

Tyvärr innebar det att eleverna behövde träffa på många nya begrepp på en gång, men jag försökte poängtera att det inte var lika viktigt att lära sig namnet ”alternatvinklar” som att känna till det faktum att sådana vinklar är lika.

Jag ritade upp en bild med två parallella linjer på tavlan, samt en linje som korsar dem. Det bildas många vinklar (åtta), men vilka av dem är lika? Jag tror eleverna redan hade en känsla för det, men det är ju viktigt i geometri att nämna vad som räknas som ett ”vetertaget faktum” (axiom) och vad som inte gör det. Jag pekade på några par vertikalvinklar och sade att de var lika, förklarade vad likbelägna vinklar var (och att det var lika), samt att det då följde att alternatvinklar var lika.

vertikal

likbelagna

alternat

Jag gjorde genomgången av alla tre begreppen på en och samma bild och dessutom lite för hastigt, eftersom jag var ivrig med att komma igång med problemlösningen. Men i efterhand ser jag att det där med ”vedertagna fakta” inte uppfattades av de flesta eleverna. Vi hade tjänat på att gå igenom dessa typer av vinklar noggrannare, långsammare och inte på en och samma bild.

Jag berättade också hur man brukar markera lika vinklar i en figur. Det spelar inte så stor roll vad man väljer för beteckning, så länge alla likadana vinklar är markerade på samma sätt. Man kan markera lika vinklar med lika många bågar eller med lika många streck på bågen eller med ett hjärta om man så vill.

Geometriuppgifter

Eleverna fick lösa uppgifter om vinklar i kanske 35 minuter. De flesta försökte på egen hand, några samarbetade och var två och två. Efter varje uppgift har jag har skrivit upp några av typiska svårigheter och frågor som eleverna (och lärarna) hade, samt hur det gick för dem att lösa uppgiften.

1. Två linjer skär varandra. En av viklarna som bildas är lika med 41°. Vad är de andra tre vinklarna lika med?

Eleverna tolkade som att bilden ”vertikalvinklar” hörde till den uppgiften (eftersom den fanns direkt bredvid). Till elever, som hade svårigheter med frågan, gav jag ledtrådar av typen ”vilka vinklar är lika på bilden?”, ”vad vet man om summan av de alla fyra vinklarna?”. Efter det hade de flesta inga problem med att lösa uppgiften.

2. Markera så många lika vinklar som möjligt i a) en kvadrat c) ett parallellogram:

kvadrat_vinklar

b) en rektangel

rektangel_vinklar

c) ett parallellogram

parallellogram_vinklar

Eleverna hade inga problem med att markera de parvis lika vinklarna (förutom en överanvändning av streck i vissa fall, en vinkel med fem överstrykningar gick inte att skilja från en vinkel med sex överstrykningar, och där gav jag rådet att använda en annan beteckning). Men nästan ingen kunde motivera varför de markerade vinklarna var lika. ”Eftersom de är lika stora”, fick jag höra några gånger. Det var helt nytt med motivering inom geometri för de flesta eleverna. Därför krävde vi inte någon rigorös förklaring på alla egenskaper hos figurerna, men stannade och diskuterade gärna om sätt att dra slutsatser på. Helt enkelt visade vi hur problemen kunde angripas strikt matematiskt.

Till exempel kunde vi fråga varför alla vinklar i mitten av kvadraten (där diagonalerna skär varandra) var lika stora och nöja oss med svaret ”kvadraten består av fyra likadana trianglar”. Men ingen refererade till ”likbelägna” eller ”alternatvinklar”, antagligen på grund av ovanan vid axiomatiskt resonerande (eller min hafsiga genomgång). Skönt i alla fall att eleverna höll med Euklides om att dessa axiom gäller :)

3. Vad är vinkelsumman i a) en triangel? b) en fyrhörning?

Här skrev de flesta eleverna ner rätt svar, men nästan ingen hade någon som helst motivering till det. På grund av detta stannade vi upp i den enskilda problemlösningen och hade en gemensam slutledning om varför vinkelsumman i en triangel alltid är 180° (ALLA visste det, men INGEN hade sett något bevis för det). Eleverna hittade på ett spännande sätt som gick ut på att kopiera triangeln och lägga den upp och ner ett par gånger. Vi behövde fortfarande använda ”alternatvinklar”-axiomet, men det sjönk nog ändå inte in att vi använde det. Det kommer ta ett tag innan gruppen är vana vid bevis!

Vad gäller förhyrningen så hade ett par elever bra idéer som gick ut på att en fyrhörning består av två trianglar (vilket ju egentligen räcker för att bygga ihop ett riktigt bevis). Vi gick igenom det på slutet av geometrimomentet och då tog jag även upp icke-konvexa fyrhörningar.

4. En linje skär två andra parallella linjer. Bestäm vinkeln mellan de mostående inre vinklarnas bisektriser.

bisektris

mostaende_inre

Eleverna som satte sig in i uppgiften kunde hitta lösningen genom att kombinera dessa två definitionsbilder. Jag kan tänka mig att om uppgiften skulle ha tagits upp på någon annan träff, så skulle en del inte kunnat lösa den. Men i samband med temat ”vinklar” och ett par ledande bilder blir den tvärtom ganska lätt.

5. Går det att rita fem strålar från en punkt så att det bildas exakt fyra spetsiga vinklar mellan strålarna? Vinklar mellan varje par av strålar räknas, inte bara mellan grannstrålarna.

Det behövdes några förtydliganden för vad som gäller i den här uppgiften, men de flesta hade en intuitiv känsla för vad strålar och spetsiga vinklar är för något. Under genomgången fick en elev komma fram och visa sitt exempel (som för övrigt inte är trivialt att konstruera). Totalt var det kanske 5 elever som hade löst uppgiften (och velat gå fram till tavlan).

6. Yttervinklarna för triangel ABC vid hörnen A och C är lika med 115° respektive 140°. En linje, som är parallell med AC, skär sidorna AB och AC i punkterna M och N. Bestäm vinklarna hos triangeln BMN.

En fråga som många av eleverna (och till med någon av lärarna!) inte visste svaret på, var vad ”yttervinkel” är för något. En av lärarna läser inte uppgifterna i förväg av pedagogiska skäl, det vill säga för att titta på uppgifterna med samma nya ögon som eleverna på lektionen. Men kanske är det inte en strategi som håller. Det var hur som helst det ordet eleverna fastnade på. Men ett par elever hann ändå klara uppgiften, med det var inte jag personligen som lyssnade igenom lösningarna.

Ladda ner för utskrift

Allt som allt var geometri och vinkeljakt ett svårt ämne, framförallt för att eleverna var så ovana. Fördelen är att alla då är på samma villkor, ingen hade mycket mer förkunskaper än någon annan. Jag hoppas att eleverna gillade att upptäcka nya saker om vinklar och bevisföring. Om någon inte gjorde det, så kan det bero att det var ett för stort kognitivt steg att direkt hoppa in i bevisens värld eller så gillade kanske inte personen att hålla på med helt nya saker (och kanske hellre ville syssla med något bekant). I det senare fallet tror jag inte Matteklubben är en rätt aktivitet för personen, då vi kommer att hålla på med nya tankesätt varje träff.

Bevis

Som jag har nämnt ovan, att motivera sina lösningar från grunden (använda sig av axiom) var någonting som var helt nytt för eleverna. När man pluggar matte möter man ofta olika typer av bevis (till exempel beviset för Pythagoras sats), men man ombes inte alltid att konstruera bevis själv. Egentligen är en motiverad lösning till vilken uppgift som helst ett bevis i sig, men brukar inte kallas för det. Därför är många universitetsstudenterna rädda för att hitta på bevis, de förstår inte hur man går till väga.

Tanken är att eleverna på Matteklubben så småningom inte ska bli rädda för att motivera saker så utförligt som möjligt. Det handlar dels att lära sig om vad som är allmänt vedertaget fakta (t.ex. behöver man inte bevisa att 1 + 1 = 2, trots att det egentligen går att motivera), med också vad som inte är det. Och dels om att bli säker på att man inte missat några möjligheter i sitt bevis. Den känslan utvecklas när man blir bra på logik och kombinatorik, vilket vi ofta övar på när vi löser blandade uppgifter.

Jag har bloggat om bevis tidigare: Vad är ett fullständigt bevis?, Att bevisa. Ett exempel på ett bevis hittar du här: Klassiska bevis: roten ur 2 irrationellt.

HMT

I samband med att tävlingen HMT hålls den 11:e november ville jag lägga ner en del av lektionen på att informera om den och att träna inför den genom att lösa gamla problem. Bara några stycken i gruppen hade hört talas om Högstadiets Matematiktävling, vilket kanske inte är så konstigt, eftersom få skolor i Uppsala har deltagit de senaste åren. (En elev som var med på första träffen hade dock gått till final förra året och presterat bra!)

Eleverna som går i Matteklubben är de mest lämpade att delta, men för att de ska kunna göra det, behöver deras lärare vara delaktiga. Därför fick alla ett informationsblad som de kunde ge till sina respektive lärare. Sista anmälningen är den 4:e november och det går att läsa mer om tävlingen på HMT:s hemsida.

Jag hoppas att några elever vill delta, de har en god chans att ta sig vidare till final! Oftast behöver man lösa ungefär 4 problem (av 6) för att gå vidare. Men det är förstås frivilligt och man ska bara tävla om man tycker att det är kul.

Övning inför tävlingen

Vi hade bara någon halvtimme kvar av lektionen för att öva på gamla HMT-problem. Men klassen hann lösa alla uppgifter en minut innan lektionen skulle sluta! Det vill säga varje uppgift löstes av åtminstone en elev. Även om jag sade att uppgifterna inte var ordnade i svårighetsgrad, så försökte de flesta ändå att lösa uppgifterna i ordningen de stod, det är ju svårt att avgöra svårighetsgraden innan man har ett hum om uppgiften.

Utvärdering

Som det märks från mängden material som vi hinner ta upp under en lektion, så kan eleverna ta in en hel del kunskap. Men de har inte riktigt lärt sig att tillämpa allt vi pratar om. Det är inte så konstigt. Det är ganska lätt att visa häftiga saker för intresserade elever, kanske berätta om sitt eget sätt att se på matte eller visa en naturvetenskaplig grej som någon annan har kommit på (sådant som förekommer på tekniska museer). Men det är svårt att lära ut genomförande, det vill säga förmågan att komma på egna häftiga saker. Det tar många år av arbete och träning.

Det är dock väldigt viktigt att ta vara på intresserade elever, eftersom de i framtiden kommer att kunna bli riktigt bra ingenjörer eller forskare (eller något annat häftigt). Målet är ju att de ska komma på nya saker och därför behöver de att träna på den förmågan. Däri ligger Matteklubbens styrka och utmaning! Det finns hur mycket som helst i matematiken som bjuder in till upptäckter, men det gäller att välja sådan material som passar eleverna. De ska ha en chans att både göra upptäckter som någon annan har gjort före dem, men också ha möjligheter för att hitta på helt nya lösningar!

Andra träffen med Matteklubben, åk 2-4

Minsta eleverna som går i Matteklubben är de i åk 2-4. Du kan också läsa om den första träffen med gruppen här på bloggen.

På den andra träffen kom färre elever, men de var precis lagom många för att vi skulle hinna prata med alla. Barn i årskurser upp till 4 är mycket aktiva och berättar gärna sina lösningar. Vi var 6 lärare och 29 elever. Ju yngre barnen är, desto lägre måste elev/lärare-kvoten vara, enligt min erfarenhet ungefär 4-5 för yngre barn och 6 (absolut högst 7) för äldre barn.

Blandade problem

Lektionen började med att eleverna satt två och två och löste blandade problem, precis som vi brukar göra med de äldre grupperna. Under varje uppgift står vanliga dialoger som jag och de andra lärarna hade med eleverna.

1. Andreas skrev upp talen i ordning tills siffran 2 skrevs upp 10 gånger. Han började med talet 1. Vilket tal slutade Andreas på?

Elev: 92, för att han började på 2, sedan är det 12, sedan 22, 32, 42, 52, 62, 72, 82, 92. Tio tal ger tio tvåor!
alternativt:
Elev: 82, för att han började på 2, sedan är det 12, sedan 22 (två tvåor), 32, 42, 52, 62, 72, 82. Tio tvåor!
Lärare: Måste tvåorna som skrivits upp alltid vara den sista siffran? (Pekar på 22.) Här är det en tvåa som talet börjar med. Finns det inte fler sådana tal?
Elev (efter en liten tankestund): Ja, just det, det är så på 20, 21, 22… Räknar snabbt fram till talet 26 (eller 27 om den andra tvåan i 22 glöms bort).

2. Så fort deltagarna ankom till Matteklubben bildades det en lång kö till fikat. Precis bakom Adam står Linda, precis bakom Linda står Hjalmar. Om man räknar från köns början, står Hjalmar som nummer tjugo. Om man räknar från slutet, står Adam som nummer trettio. Hur många personer står i kön till fikat?

Elever: Är svaret 46?
Lärare: Kanske, berätta hur ni tänkte!
Elever: Om Adam är nummer 30 från slutet, så är det 27 personer bakom Hjalmar i kön. På samma sätt är det 17 framför Adam. Mellan Adam och Hjalmar är det 2 (personer). Tillsammans blir det 27 + 17 + 2 = 46.

(Det fanns också andra förklaringar till 46 som jag måste erkänna att jag inte riktigt förstod. Det var inte helt lätt att fånga upp felet i resonemang där man är slarvig med att räkna med/inte räkna med personer som står på ändarna)

Lärare: Vilka personer har vi räknat in och vilka har vi inte räknat in? Har vi räknat någon två gånger?
alternativt:
Lärare: Om det är 27 personer bakom Hjalmar, hur många är resten? Alltså från nummer 1 till Hjalmar som är nummer 20? (Det var inte helt självklarat för vissa barn att det var 20.)

3. Med hjälp av siffrorna 0, 5 och 9 bilda det största möjliga samt det minsta möjliga tresiffriga talet. Siffrorna i talet måste alla vara olika.

Elev: Det är 905 och 059.
Lärare: Men 059 räknas inte som tresiffrigt.
Elev: Aha, då är det 509.

4. Tre ekorrar hittade 90 nötter. De delade upp nötterna på så sätt att den äldsta ekorren fick 10 nötter mer än mellanekorren och så att den yngsta ekorren fick 10 nötter mindre än mellanekorren. Hur många nötter fick varje ekorre?

ekorre

Elever: Vi tänkte först att alla skulle få lika många nötter, 30 stycken. Men sedan skulle den minsta ge 10 till den största, så det blev 40, 30, 20.

alternativt:

Elever: Vi testade med 30, 20, 10, men då blev det för lite. Det saknas 30 nötter. Då lade vi på 10 till varje ekorre.

5. På en idrottslektion ställde sig hela klassen på en rad. Först skulle var sjunde barn göra två steg fram. Sedan skulle var tredje barn (av de som var kvar i ledet) göra ett steg fram, och till sist skulle var femte barn (av de som var kvar) göra ett steg bakåt. Hur många går i klassen om 15 barn stod kvar på sina platser i slutändan?

Elever: Är svaret 30?
Lärare: Låt oss kontrollera!
(Vi kontrollerar för 30 genom att rita upp 30 pinnar/saker, stryker dem en i taget och ser att det fungerar.
Lärare: Finns det fler svar?

Ladda ner för utskrift

Några av elevparen blev klara med uppgifterna snabbt, och då fick de lösa ett par extra uppgifter från träffen med åk 5-6.

Sedan var det dags att presentera lösningarna på tavlan. Många av eleverna/grupperna var ivriga att få gå fram. För att fler skulle få komma fram fick de göra det två och två. De som var bekväma med att prata inför gruppen fick presentera lösningen, de andra agera som stöd (ibland turades båda om att prata).

Eleverna hade snygga (förfinade efter diskussion med läraren) lösningar på uppgifterna. Till exempel, på uppgift 1 skrev de bara upp talen från 1 till 26 som innehöll siffran 2 (eftersom de andra var irrelevanta). På uppgift 2 ritade eleverna upp hur de tänkte, vilket nästan påminde om Venn-diagram, man kunde lätt följa deras resonemang. Efter att uppgift 3 hade presenterats frågade jag hur man i allmänhet bildade största möjliga och minsta möjliga tal med en given mängd siffror. Barnen kunde svara på det utan problem, även om vissa först tänkte att 0 kunde stå på första plats i ett tal (även någon enstaka lärare trodde att det var ok).

Fixering vid svar

Det jag har märkt både under diskussionerna med eleverna och i sättet de presenterar lösningarna på tavlan är att de lägger stor vikt vid att formulera svaret. De tycker att det absolut ska stå ”Svar:” någonstans på pappret (eller när man presenterar på tavlan). Eller så glömmer de ibland bort att skriva det, men när de är färdiga med lösningen kommer de ihåg att avsluta med ”Svar: 30 elever” till exempel.

Detta läggs förstås vikt på i skolan, för att läraren lätt ska få en överblick över om uppgiften gjorts rätt eller inte. Under Matteklubben försöker jag skifta fokus från svar till själva lösningar. På frågan ”Är __ rätt svar” svarar jag alltid ”Hur tänkte ni?” för att visa att det är tanken och inte vad man räknade ihop på slutet, som räknas. Extra roligt är det att ta med uppgifter där det finns flera svar på lektionerna. Då förstår eleverna bättre när läraren ställer frågorna ”Finns det fler svar på uppgiften? Varför/varför inte?”. De börjar undersöka mer för att själva försäkra sig om att de verkligen har betraktat alla möjligheter. Vi straffar inte elev för att hen har gissat sig fram till ett svar, för det är också en slags strategi (som kan ge rätt svar), men vi försöker säga att det inte räknas som en fullständig lösning förrän man är säker på att det inte finns fler svar.

Det var det som hände vid diskussionen av uppgift 5, då vi kom fram till att det finns ett ytterligare svar än det som presenterades på tavlan. Men därefter kunde vi också förklara varför antalet elever i raden inte kunde bli större eller mindre.

Experiment med utvikningar

Nu fick eleverna vara i gruppen om 3-5 och undersöka olika utvikningar. Varje grupp fick en sax och en linjal, samt papper för att klippa ut och testa utvikningar. Till uppgift 2 tog jag med en Rubiks kub som fick stå framme på katedern. Om man ville testa sin utvikning, fick man alltså komma fram och göra det. Till uppgift 3 tog jag med några tändsticksaskar (därav måtten) som eleverna också kunde testa utvikningar på. Men det var nästan ingen som hade kommit så långt.

Eleverna var lite mer trötta vid det här laget och hade svårigheter med att läsa igenom och skilja på de olika uppgifterna. Jag sade till många att de skulle komma på egna utvikningar, men då läste ju inte eleverna uppgift 2 så noga (eftersom de antog att de redan hade fått det förklarat) och många missade att sidan skulle vara 6 cm. Inte för att det gör särskilt mycket. Men nästa gång ska jag ha tydligare gräns mellan uppgifterna, kanske till och med ge ut dem en i taget.

1. Vilka av figurerna på bilden kan vecklas ihop till en kub?
kuber1

Vissa elever föreställde sig hur det skulle bli i huvudet (och då gjordes såklart också några fel) och kunde utesluta eller godkänna några former. De flesta klippte ut och testade med papper när de var osäkra. Den metoden fungerade perfekt. Några av eleverna sade att de redan hade gjort liknande uppgifter tidigare på lågstadiet och då kan man ju bara glädjas åt att de verkar ha haft roligt då i skolan. Jag hoppas dock att alltid lära ut något extra med uppgifterna på Matteklubben, så som diskussionen nedan.

2. Hitta på en annan utvikning till en kub och tillverka den. Kubens sidor är 6 cm långa. Klipp ut din utvikning och testa den på kuben.

kub

Några grupper gjorde en egen utvikning i rätt storlek, några gjorde mindre utvikningar. Det bästa med stora utvikningar var att vi kunde testa dem på Rubiks kub och alla kunde se att det passade. Många grupper hittade den utvikningen, som är lik den första, fast man flyttar två av rutorna (så att formen ser ut som bokstaven ”T”). Då uppmanade jag dem att hitta på en till.

3. Kom på en utvikning till ett rätblock som är 1,5 cm hög, 4 cm bred och 5,5 cm lång. Klipp ut och testa utvikningen!
Under tiden någon klipper ut utvikningen, försök att komma på fler annorlunda utvikningar till samma rätblock. Du behöver inte rita dem snyggt, bara på ett ungefär.

En grupp tillverkade utvikningen och vi testade den sedan på tändsticksasken. Möjligen hade de flesta grupper inte hunnit komma så långt, då vi inte hade så mycket tid för det här momentet.

Ladda ner för utskrift

Diskussion

Vi ritade upp alla utvikningar (inklusive de falska) från uppgift 1 på tavlan och gick igenom dem en och en och klassen fick skandera ”ja” eller ”nej” som svar på frågan huruvida de var möjliga eller inte. De flesta hade alla rätt. Vi markerade även vilka rutor som var tvungna att överlappa ifall man skulle klippa ut figuren och försöka vika en kub utav den.

Sedan var det dags för grupperna att lämna in utvikningar som de själva hade kommit på. Det blev tre annorlunda former totalt och de ritade vi upp (och visade upp de stora). Jag berättade att det totalt finns 11 utvikningar så om man ville, kunde man försöka hitta de 2 vi saknade. Här bifogar jag en bild över alla ifall man är nyfiken:

11nets_cube

Sedan visade vi upp utvikningen för ett rätblock som en grupp hade gjort (som var korrekt och inspirerad av standardformen (”plus”) på kubutvikningen). Då ställde vi en fråga till barnen: ”Tror ni att finns fler utvikningar för en rätblock än för en kub eller färre?”. ”Färre!” skanderade barnen. De tänkte att det var svårare att rita upp en utvikning för ett rätblock (svårare att passa in sidor), alltså måste det finnas färre sådana.

Då försökte vi diskutera fram till att om en utvikning för ett rätblock kan göras av en kub-form, skulle en inte då kunna göras av andra kubformer också? Långsamt blev barnen mer och mer övertygade om detta. ”Lika många, lika många!” skrek de då.

Sedan ritade jag och en annan lärare upp flera olika former för rätblock som egentligen hade samma underliggande standardutvikningsform för kuben. Vi kunde variera den på minst tre olika sätt, genom att välja form och riktning på ”sidoflärparna” (det finns ju tre olika rektangelytor). Då började fler och fler barn långsamt bli övertygade om att de faktiskt fanns fler former för rätblock (som inte är kuber) än för kuber. Jag avslöjade att det fanns ungefär 50 utvikningar för rätblock. ”Och vi ska hitta de alla!” sade en elev med uppspärrade ögon. Kul tänkt, men matte ska ju helst inte var plågsamt :) Så det behövde de förstår inte göra, men jag bifogar de ändå här:

block

Hemuppgift

Det fanns extrauppgifter på bladet som de flesta inte hann komma till. Därför fick de ta dem med sig hem och tänka över dem i lugn och ro. Hemuppgiften är förstås frivillig.

Konstig nog går även den här formen att vika ihop till kub (testa hemma)!

utv0

Kan följande former också vikas ihop till kuber?

utv1

utv2

Jag berättade om vad den första uppgiften gick ut på (att man skulle klippa ut den delen som var i färg). Barnen blev väldigt förvånade över att det var en utvikning (”hur ska man vika ihop den då?”). Då tipsade jag om att det fanns en ritning över kuben, som var sned och att man kunde ta den som grund. Då förstod en av eleverna att de bitarna som stack ut passade ihop precis med det som saknades på rutorna bredvid. Får se om någon tar sig an de sista tre formerna och lyckas vika ihop dem till en kub. Det är inte särskilt lätt ens för vuxna!

Utvärdering

De 29 eleverna som kom till lektion kände sig motiverade och trivdes bra (förutom för en elev som var där för första gången och inte hade roligt), så gruppen är rolig att arbeta med. Nivån var till och med enkel för många, så det gäller att ha ett förråd med svårare uppgifter, ifall någon blir klar väldigt fort (t.ex. uppgifter från åk 5-6 kan passa). Barnen blev fortfarande trötta mot slutet, men eftersom uppgifterna var mer tillgängliga än första gången, orkade nästan alla jobba hela vägen fram.

En annan lärare påpekade, efter att han på en rast hjälpt en elev att fatta lösningen på uppgiften om fikakön, att det viktigaste med matten är inte att fatta, utan att försöka fatta. Kloka ord tycker jag, Har man nyfikenheten och ihärdigheten, så kan man komma hur långt som helst!

Andra hemuppgiften från Matteklubben, åk 5-6

Här i kommentarerna kan du diskutera hemuppgiften. Skriv om du har frågor eller förslag på lösning/svar.

• En viss figur hade arean 12 cm². Om den figuren förminskas så att alla dess sidor bli hälften så stora, vad kommer dess area att bli då?

• Rita figur som har 2 gånger så stor area som figuren på bilden, men har samma form.

rutat_papper04

Ladda ner för utskrift

Andra träffen med Matteklubben, åk 5-6

36 elever och 6 lärare

Denna gång var det 36 elever som var närvarande, vilket är närmare ett lagom antal än förra gångens 41. Vi var sex stycken lärare och jag tror att vi räckte till det mesta av tiden. Om uppgifterna hade varit för lätta, så skulle vi inte ha så mycket att diskutera med barnen, förutom att de skulle berätta hur de tänkte (och vi skulle förmodligen inte hinna lyssna på allas lösningar). Och om uppgifterna hade varit för svåra så skulle vi inte lärarna ha så mycket att göra annat än att tipsa eleverna om hur de kan tänka. Det är lagom nivå på uppgifter om eleverna löser några, tänker fel på några andra (så att de lär sig något nytt!) och kanske har svårt för att lösa de allra svåraste problemen på egen hand, så att de börjar utbyta idéer med varandra. Vi kunde även lyssna på några elever som inte hittade någon att samarbeta med (eller inte ville samarbeta, vi tvingande ingen att vara i grupp, bara uppmanade). Jag hann i alla fall själv att prata med nästan alla grupper åtminstone en gång, vilket borde betyda att de flesta grupper har hunnit bolla var och en av sin idéer med åtminstone någon av lärarna.