Kategori: Problemlösning

Lösningen till problemet för de äldre vecka 47

Mattegåta

I tio likadana kannor finns lite mjölk: varje kanna är full till max 10%. En tillåten operation är att ta en valfri kanna och hälla av en del av mjölken till de andra kannorna (lika mycket till varje övrig kanna).

Visa att 10 operationer räcker för att få kannorna att innehålla exakt lika mycket mjölk.

Diskussion

För det första kan kannorna innehålla väldigt ojämna mängder av mjölk, så det, att kannorna är fulla till max 10%, säger är att vi alltid kan hälla över mjölk, det blir alltså aldrig för fullt i någon kanna.

Vi ska få till lika mycket mjölk i varje kanna. Det känns inte som om vi kan hoppas på den sista överhällningen. Om det är ojämnt i många kannor, kan inte en enda överhällning (som ju häller lika mycket i varje icke-vald kanna) få alla kannorna att innehålla lika mycket. Alltså måste vi börja fixa kannor med lika mycket mjölk redan i början.

Börjar man på ett smart sätt får man att 9 operationer räcker.

Lösning (av Erik Svensson)

För att fördela mjölken jämnt mellan kannorna, låt oss använda följande algoritm:

Om alla kannorna har lika mycket mjölk i sig, då är vi klara. Annars kommer någon kanna ha mest mjölk och någon annan ha minst mjölk (om flera har mest eller minst väljer vi godtyckligt bland dessa), och mellan dem finns en viss skillnad i hur mycket mjölk de innehåller. Från den med mest mjölk häller vi till varje annan kanna en tiondel av denna skillnad. På det viset kommer den mest mest mjölk förlora nio tiondelar av skillnaden, och den med minst mjölk ökar med en tiondel av skillnaden, och således kommer de efteråt att innehålla lika mycket mjölk. Alla kannor, utom den vi häller ifrån, ökar sitt mjölkinnehåll lika mycket, vilket innebär att den kanna som hade minst mjölk innan operationen fortfarande kommer ha minst mjölk, tillsammans med den som nyss hade mest mjölk.

Sedan upprepar vi detta. För varje iterering tar vi den kanna som har mest mjölk och ser till att den jämnställs med alla kannor som har minst mjölk. Dessa kannor ändras inte i förhållande till varandra, och alltså kommer vår algoritm på detta vis att öka antalet såna jämnställda kannor med ett vid varje iterering. Efter högst tio itereringar kommer således alla kannor innehålla minst mjölk, det vill säga, de innehåller alla lika mycket mjölk.

Lösningen till problemet för de yngre vecka 46

Mattegåta

När Dag tog studenten, fick han en klocka som hade en timvisare, en minutvisare och en sekundvisare. Hur många gånger per dygn sammanfaller alla tre visarna? (Förklara varför.)

Diskussion

Det här var ett svårt problem. Ett förvirrande faktum är vi måste studera tiden i dubbel bemärkelse. Problemet hade egentligen varit densamma ifall tre löpare hade sprungit med olika hastigheter runt en bana. Vi undrar när alla tre träffas, så vi kommer betrakta visarna som löpare.

Hur snabba är de då? Sekundvisaren är snabbast och ”springer” med hastigheten ett steg per sekund (stegen är de 60 markeringarna på klockan). Sedan kommer minutvisaren som tar en sextiondedels steg per sekund och långsammast är timvisaren, som ”promenerar” med hastigheten 1/720 steg per sekund (5 steg per timme eller 60 steg på 12 timmar). Nu kan vi pilla med hastigheterna om vi vill för att se när de olika visarna träffar varandra.

Lösning

Vi kan börja med att undersöka när två av visarna, minutvisaren och timvisaren, träffar på varandra under ett dygn. De börjar klockan 0:00 på samma ställe, på tolvan, och sedan rycker minutvisaren iväg. Eftersom minutvisaren klarar av 60 steg på en timme, medan timvisaren tar 5 steg, kommer de att träffas nästa gång efter mer än 1 timme. Mer exakt tar det faktiskt 12/11 av en timme. Minutvisaren drar iväg sedan och kommer gå om timvisare med jämna mellanrum.

Så minut- och timvisaren träffas:
1. efter 0 timmar (de börjar på samma ställe)
2. efter 1 och 1/11 timme
3. efter 2 och 2/11 timme
4. efter 3 och 3/11 timme
5. efter 4 och 4/11 timme
6. efter 5 och 5/11 timme
7. efter 6 och 6/11 timme
8. efter 7 och 7/11 timme
9. efter 8 och 8/11 timme
10. efter 9 och 9/11 timme
11. efter 10 och 10/11 timme
12. efter 11 och 11/11 timme = 12 timmar
13. efter 13 och 1/11 timme
14. efter 14 och 2/11 timme
15. efter 15 och 3/11 timme
16. efter 16 och 4/11 timme
17. efter 17 och 5/11 timme
18. efter 18 och 6/11 timme
19. efter 19 och 7/11 timme
20. efter 20 och 8/11 timme
21. efter 21 och 9/11 timme
22. efter 22 och 10/11 timme
23. efter 23 och 11/11 timme = 24 timmar, vilket är ett nytt dygn, så det räknas inte!

Så minutvisaren och timvisaren träffas 22 gånger per dygn, men vilka av gångerna hakar sekundvisaren på?

Vi kan kolla på vilka positioner sekundvisaren hamnar efter perioder på 1 och 1/11 timme. Sekundvisaren har hastigheten 3600 steg per timme, så totalt kommer den gå en massa varv plus 3600/11 steg som är lika med 327 och 3/11 steg som är lika med 5 varv och 27 och 3/11 steg. Så på klockan kommer visaren att hamna mellan femman och sexan nånstans. Vi kollar alla situationer då timvisaren sammanföll med minutvisaren:

1. sekundvisaren är på 0 steg = prick på klockan 12!
2. sekundvisaren är på 27 och 3/11 steg = mellan kl 5 och kl 6
3. sekundvisaren är på 54 och 6/11 steg = mellan kl 10 och kl 11
4. sekundvisaren är på 21 och 9/11 steg = mellan kl 4 och kl 5
5. sekundvisaren är på 49 och 1/11 steg = mellan kl 9 och kl 10
6. sekundvisaren är på 16 och 4/11 steg = mellan kl 3 och kl 4
7. sekundvisaren är på 43 och 7/11 steg = mellan kl 8 och kl 9
8. sekundvisaren är på 10 och 10/11 steg = mellan kl 2 och kl 3
9. sekundvisaren är på 38 och 2/11 steg = mellan kl 7 och kl 8
10. sekundvisaren är på 5 och 5/11 steg = mellan kl 1 och kl 2
11. sekundvisaren är på 32 och 8/11 steg = mellan kl 6 och kl 7
12. sekundvisaren är på 59 och 11/11 steg = 60 steg = 0 steg = prick på klockan 12!
Sedan upprepar historien sig!

Ingenstans, förutom klockan 12 på natten och på dagen hamnar sekundvisaren ens mellan rätt siffror (t.ex. i situation 8 är sekundvisaren mellan kl 2 och kl 3, medan minut- och timvisaren är mellan kl 7 och kl 8). Detta betyder att alla tre visarna träffas exakt två gånger per dygn!

Lösningen till problemet för de äldre vecka 46

Mattegåta

Visa att varje andragradspolynom kan skrivas som en summa av två andragradspolynom, vars diskriminanter är lika med 0.

Diskussion

Vad var en diskriminant? För ett polynom Ax²+Bx+C är det talet B²-4AC.

Ifall diskriminanten är positiv, så har ekvationen Ax²+Bx+C=0 två reella rötter. Ifall den är negativ, så har ekvationen inga reella rötter. Om diskriminanten är 0, har ekvationen exakt en reell lösning.

Bilden illustrerar hur graden för ekvationen kan se ut i de olika fallen (D betecknar diskriminanten).

Nu när vi har koll på diskriminanten, kan uppgiften lösas grafiskt eller algebraiskt, vilken man nu föredrar. Nedan är en algebraisk lösning presenterad.

Lösning (av Benjamin Fayyazuddin-Ljungberg)

Låt P(x) vara polynomet vi vill skriva som summan av två andra polynom. Om P(x) = Q(x) + R(x) är kP(x) = kQ(x) + kR(x). Om Q(x) har diskriminant noll har kQ(x) också det. Därför kan vi utan inskränkning anta att P(x) har koefficienten 1 framför x²-termen.

Nu betraktar vi tre fall:

1) P(x) har diskriminant noll. Då har vi inga problem: P(x) = P(x)/2 + P(x)/2

2) P(x) har negativ diskriminant, det kan skrivas som (x-a)² + k² för någon konstant k. Låt z=x-a, så P(x) = z² + k². Då kan vi skriva P(x) som (z+k)²/2 + (z-k)²/2 = (x-a+k)²/2 + (x-a-k)²/2. Det är tydligt att de här polynomen bara har ett nollställe var, alltså är diskriminanten noll.

3) P(x) har positiv diskriminant, det kan skrivas som (x-a)² – k² för någon positiv konstant k. Låt z = x-a igen. Då är P(x) = z² – k². Vi skriver P(x) som 2(z-k/√2)² – (z-k√2)² = 2(x-a-k/√2)² – (x-a-k√2)². Dessa har också bara ett nollställe var, så de har diskriminant noll.

Lösningen till problemet för de yngre vecka 45

Mattegåta

En chokladtårta är rektangelformad och sju personer ska dela på den. På tårtan finns 7 marsipanrosor:

Hur kan man dela tårtan i sju delar så att det finns en ros i varje del, om man bara får skära tårtan tre gånger och skärningarna måste vara raka linjer? Observera att delarna inte behöver vara lika stora.

Diskussion

Om det till en början inte verkar gå med tre linjer, tänk på vad tre linjer kan bilda för konfigurationer vid sidan av tårtan. Tre linjer som inte korsar varandra i en och samma punkt och som inte är parallella bildar en triangel och sex oändliga delar om de ritas på ett oändligt plan.

Sju är det maximala antalet delar, så linjerna på tårtan ska bilda någon liknande figur (det ska vara en ros i varje del).

Ett annat sätt att komma fram till svaret är att rita en linje i taget. Om man tänker från slutet, måste varje del på tårtan innehålla högst två rosor innan sista linjen ritas (så att den eventuellt skär på dessa delar). På samma sätt, måste varje del innehålla högst fyra rosor innan den andra linjen ritas. Så den första linjen som ritas måste dela tårtan i två delar: en med tre rosor och en med fyra.

Lösning (av Nicklas Yttergren)

Så här till exempel:

Lösningen till problemet för de äldre vecka 45

Mattegåta

Ett biljardbord har en långsida som är dubbelt så lång som kortsidan. I varje hörn finns det ett hål, samt två hål till finns på varje långsidas mitt.

Vilket är det minsta antalet bollar som man kan placerat ut på bordet så att varje hål befinner sig på samma linje som ett visst par av bollar? (Bordet är rektangulärt, hål och bollar antas vara lika stora som punkter.)

Diskussion

Eftersom det frågas efter det minsta antalet i uppgiften är det underförstått att resultat skall bevisas. Det vill säga det måste finnas ett exempel med x bollar (om x är svaret), samt bevis för att det inte går med färre än x bollar.

Ett sätt att jobba på är att börja underifrån (till exempel med 1 eller 2 bollar) och för varje antal antingen visa att det inte går eller att det går. Fallen är oftast svårare närmast svaret. Lite som i fyrfärgsproblemet!

Fyrfärgsteoremet

Sats. För en platt ”karta” räcker det alltid med fyra färger för att måla ”länderna” på kartan så att inga två länder med gemensam gräns har samma färg (gränser utgörs av raka eller krokiga linjesegment).

Det var länge känt att det räckte med fem färger och att det finns kartor som inte går att färga med tre färger. Men fallet fyra tog lång tid tills den äntligen bevisades med hjälp av datorberäkningar.

Lösning (av Erik Svensson)

Till att börja med kan vi uppenbart utesluta att det går med bara en boll (och förstås även med noll bollar).

Det finns ej heller någon lösning för två bollar, ty vi vet att två bollar (punkter) entydigt bestämmer en linje, så om samtliga hål ska ligga i linje med två bollar, då måste alla hålen ligga på samma linje. Men hålen på biljardbordet ligger inte på en linje.

Det är inte heller möjligt med tre bollar, vilket vi ser om vi försöker konstruera en. Om vi har tre bollar, då finns det två möjligheter: Att de ligger på en linje eller att de inte gör det.

Ifall de ligger på en linje, då får vi en motsägelse med samma resonemang som för två bollar, och ifall de inte ligger på en linje så bildar de en triangel. I så fall utgör varje linje med två bollar en sida i denna triangel, och bollarna är hörnen.

Vi börjar med att konstatera att ingen sida i denna triangel kan täcka tre hål, ty de enda linjerna på bordet som täcker tre hål är långsidorna. Ens om vi antar att frågeformuleringen tillåter bollar längs med sidorna innebär detta att två bollar måste ligga på en av långsidorna, vilket innebär att den tredje bollen måste ge upphov till två linjer som täcker samtliga tre resterande hål, vilket medför att någon av dessa två linjer måste täcka två hål på den andra långsidan och ändå korsa den första långsidan, vilket är omöjligt.

Att täcka fyra eller fler hål med en linje är förstås också omöjligt som biljardbordet är uppbyggt.

En linje kan ej heller passera genom bara ett hål, eftersom detta lämnar fem hål att täckas med de resterande två linjerna, och alltså måste någon av dessa linjer täcka minst tre hål, vilket motsäger det vi just kom fram till. Även en linje som inte täcker några hål kan vi utesluta, eftersom denna linje i så fall kan tas bort och därmed ge en lösning för två hål, vilket vi visat inte existerar.

Således måste vi ha tre linjer som täcker exakt två hål, och de måste täcka två bollar vardera. Eftersom varje boll är ett hörn i den triangel som bildas ligger varje boll på två sådana linjer.

På bilden ser vi alla möjliga linjer som täcker två hål, samt alla skärningspunkter mellan dem. Dessa punkter är de enda kandidaterna till var en boll kan ligga. Vi ser emellertid att det inte finns någon triangel av sådana punkter (med de utmarkerade linjerna som sidor), och den minsta slutna figur vi kan bilda är en fyrhörning. Alltså finns det ingen lösning för tre bollar, men det finns en för fyra, till exempel genom att välja fyra punkter som bildar en fyrhörning i bilden och lägga bollarna där.

Lösningen till problemet för de yngre vecka 44

Mattegåta

Fem fotbollslag spelade en turnering, där alla lag mötte alla en gång. För en vinst tilldelades 3 poäng, för oavgjort 1 poäng och för förlust gavs inga poäng.

Fyra av lagen fick 1, 2, 5 och 7 poäng respektive. Hur många poäng fick det femte laget?

Diskussion

I alla för mig blir det lättare att lösa turneringsproblem, om man ritar en graf eller en tabell över resultaten.

Till exempel vet vi att ett av lagen fick 1 poäng, då kan man utan inskränkning anta att det är Lag 1. Då ser deras rad i tabellen ut som nedan.

Kolonnen är på sätt och vis motsatsen, alla förluster byts mot vinster (Lag 3, 4 och 5 vann ju mot Lag 1). Problemet går ut på att ta reda på sista radens poängsumma!

Lösning (av Nicklas Yttergren, kompletterad)

Observera hur många matcher har förlorats och hur många vunnits, de måste ha varit lika många. Totalt var det 7 förluster och 3 vinster utan att man räknat med med det femte laget (det ser man på poängen 1=1+0+0+0, 2=1+1+0+0, 5=3+1+1+0, 7=3+3+1+0).

Då måste det femte laget vunnit alla sina matcher, eftersom de spelade fyra och det är precis så många vinster som saknas. Därför fick de 12 poäng.

tabellresultat
Så kan det se ut

Lösningen till problemet för de äldre vecka 44

Mattegåta

Martin samlar på ovanliga mynt. Mynten i hans samling alla har en diameter på högst 10 cm. Samlingen förvarar han i en låda som har storlek 30 cm x 70 cm (i ett lager, inga mynt ligger ens delvis ovanpå varandra).

Men nyss fick Martin ett nytt mynt med en diameter så stor som 25 cm. Visa att den nya samlingen får plats i en låda som är 55 cm x 55 cm stor (också nu i ett lager).

Diskussion

Uppgiften handlar lite om att optimera. Om vi har eventuell platsbrist i den nya lådan, så är det nog lite dumt att lägga det stora 25 cm x 25 cm-myntet i mitten utav den. Mycket smartare är det att lägga det i ett hörn.

Mynt kan även ligga på krångliga sätt, de är ju cirklar av olika storlekar. I varje mellanrum går det att stoppa in ett pyttelitet mynt till. Därför är det omöjligt att uppskatta antalet mynt och även hopplöst att försöka omplacera mynten för mycket.

Så gissningsvis ska mynten ligga ungefär som de gjorde i första lådan. Och det stora myntet ska ligga i ett hörn. Dessa två antaganden leder fram till lösningen nedan.

Lösning (av Benjamin Fayyazuddin-Ljungberg)

Rita ett rött streck 15 cm in på Martins ursprungliga låda, så att den delas in i två delar av storlek 30cm*55cm och 30cm*15 cm. Rita ett parallellt blått streck, 10 cm längre in än det röda, så att vi får två delar av storlek 30cm*45cm och 30cm*25cm.

Dela in lådan två (överlappande) rutor, ett som begränsas uppifrån av överkanten på lådan och nedifrån av det blåa strecket (storlek 30cm*25cm), och ett som begränsas uppifrån av det röda strecket och nedifrån av nederkanten på lådan (storlek 30cm*55cm).

Eftersom mynten högst har diameter 10 cm kan det inte finnas något mynt sådant att det röda strecket och det blåa strecket båda passerar genom det. Därför kan vi säga att varje mynt tillhör den rutan som helt innefattar det myntet. Alla mynt tillhör då någon ruta, och får plats i den. Det kan finnas mynt som hamnar i båda rutorna, då kan man godtyckligt välja vilken ruta de ska tillhöra.

Nu flyttar vi runt rutorna, med alla tillhörande mynt, och placerar dem i Martins nya låda. Vi ser då att vi får plats med en gul ruta i hörnet med storlek 25cm*25 cm. Alltså får det nya myntet plats också.

Sonja Kovalevsky-dagarna i Stockholm 2010

Sonja

För tredje gången i rad var jag med och ordnade problemlösning (tillsammans med Dag Jonsson, Magnus Carlson och min pappa) på Sonja Kovalevsky-dagarna. Tredje gånget gillt verkar det som.

Dessa dagar har som syfte att visa varför det är bra att läsa matematik och vad matematik kan användas till. Massa gymnasieungdomar från hela Sveriges samlas på något universitet (Stockholms i år) och får gå på föreläsningar och workshops.

En tradition (kanske 8 år tillbaka, nåt sånt) är att ha en liten tävling under de här två dagarna. På fredagen får eleverna en lista med problem och både under fredagen och lördagen får de lösa dem i små lag och lämna in dem.

De lag som utmärkt sig mest får priser, i år fick de en problemlösningsbok. Det visade sig att en av pristagarna redan hade boken .. med sig .. kanske därför vann han.

Annorlunda för i år jämfört med de tidigare två åren var att vi hade 1,5 timmars sessioner med varje grupp (som bestod av 4-6 lag) då de fick redovisa uppgifterna muntligt. Problemlösningsdelen på Sonja Kovalevsky-dagarna brukar ändå vara uppskattad (för att den står ut lite från det övriga programmet), men de mutliga redovisningarna tror jag gjorde det ännu bättre.

Även om det hela var lite kaotiskt ordnat, vilket hör dagarna till, så fick vi massor med bra direktrespons. Eleverna tyckte att uppgifterna var roliga och annorlunda, de fick tänka på nytt sätt. Samtidigt fick de träna i mutlig redovisning av slutledningar och tankar, något som inte alltid förekommer på vanliga mattelektioner.

Det var helt enkelt något nytt och svårt, men överkomligt för många av dem, de var trots allt de mest matematikintresserade eleverna i Sverige.

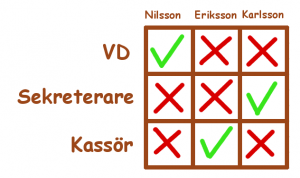
Testa själv att lösa problemen från Sonja Kovalevsky-dagarna 2010.
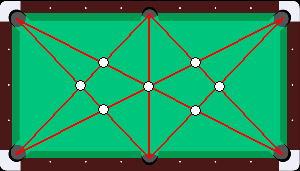
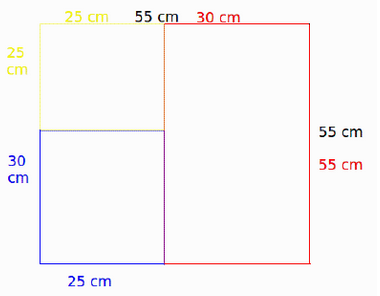
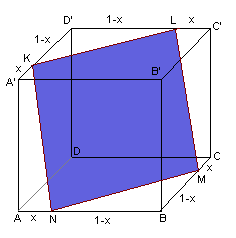
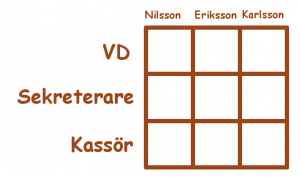
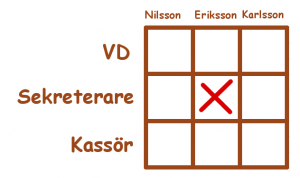
Ni känner kanske igen det första problemet, det har varit med på bloggen förut.

Antingen tävlar du på medelsvår nivå, då ska du lösa minst ett kvalproblem och så många medelsvåra problem som möjligt. Eller så tävlar du på svår nivå och då ska du lösa minste ett problem från varje föregående del. Observera att de svåra problemen verkligen är svåra!

Lösningarna kommer att läggas upp så fort de redigerats klart. Än så länge kan jag kontrollera era lösningar om ni skickar de till mig.

Lösningen till problemet för de yngre vecka 43

Mattegåta

Tre vänner har ett företag ihop. Deras efternamn är Eriksson, Karlsson och Nilsson. En av dem är VD, en är sekreterare och en är kassör. Sekreteraren har inga syskon och han är den yngste på företaget. Nilsson är äldre än kassören och är gift med Erikssons syster.

Bestäm VD:ns, sekreterarens och kassörens respektive efternamn.

Diskussion

Problemet är ett typiskt exempel på en mysteriegåta. Det kanske inte är särskilt stor mystik över vem som verkligen är VD på företaget, men det är i vilket fall okänt för oss.

Om du inte vet var du ska börja, rita en tabell över alla möjligheter:

Målet att vi ska välja exakt en ruta i varje rad och varje kolonn. Då kommer precis en person bli kassör, en sekreterare och en VD.

Men först måste några rutor uteslutas.Till exempel sekreterare-Eriksson-rutan (tänk på varför).

Fortsätter du på detta vis får du fram vilka rutor som är fel och vilka som är rätt. Lösningen med svaret finns längst ner.

Gillar du sådana här problem rekommenderar jag ett beroendeframkallande spel Sherlock – The Game of Logic. På sidan kan ni ladda ner ett demo och prova att spela.

Spelet går ut på sammaställa en unik person med en unik frukt, ett hus, en siffra och lite andra grejer. Till sin hjälp har man massa olika ledtrådar på den högra sidan av skärmen. De kan säga vilka saker som finns bredvid varandra (till exempel kolumnen med R måste vara bredvid kolumnen med det röda huset), ifall något är till vänster om något annat, ifall tre saker inte ligger efter varandra (åt något håll). Det finns alltid en unik lösning på slutet!

Lösning (av Toomas Liiv)

Sekreteraren har inga syskon och är yngst. Nilsson är äldre än kassören och kan därför inte vara yngst. Nilsson är gift med Erikssons syster. Eriksson har alltså minst ett syskon. Sekreterarens kriterier passar inte in på vare sig Eriksson eller Nilsson och måste därför vara Karlsson.

Nilsson är äldre än kassören och kan därför inte vara kassör, förutsatt att han inte är äldre än sig själv. Den enda kvarvarande möjligheten är VD, vilket han då också måste vara.

Kvar finns Eriksson och kassören som då måste vara samma person.

Alltså har vi att:

• VD:ns namn är Nilsson

• Sekreterarens namn är Karlsson

• Kassörens Eriksson

© 2009-2024 Mattebloggen