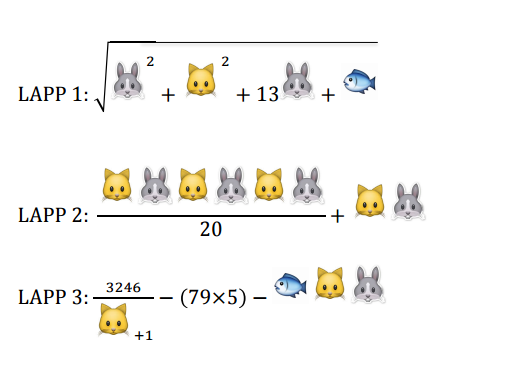Jämn siffra efter udda
Vanda skrev talen från och med 1000 till och med 2000 i ordning på en rad som ett enda långt tal:
1000100110021003….19992000
Hur många gånger skrev hon en jämn siffra direkt efter en udda siffra?
(Jämna siffror är 0, 2, 4, 6, 8; udda siffror är 1, 3, 5, 7, 9).
Bussar på vägen
Bussar på vägen
Lars går längs med en väg med konstant hastighet. Var 6:e minut ser han en buss som åker förbi honom och var 3:e minut möter han en buss som åker åt andra hållet. Bussarna åker med samma fart åt båda håll och startar från ändhållplatserna med jämna mellanrum. Hur långa är dessa mellanrum?
Ihoplimmad kub
Ihoplimmad kub
Av 27 kuber av storleken 1x1x1 limmade man ihop en kub av storleken 3x3x3 genom att alla kontaktytor limmades. För att limma ihop två sidor använde en droppe lim varje gång. Hur många droppar lim använde man totalt?
Skolsteg
Skolsteg
Maria, Jakob och deras pappa går till skolan tillsammans. Under tiden som pappa tar 3 steg, så tar Maria 5 steg. Under tiden som Maria tar 3 steg, så tar Jakob 5 steg. Maria och Jakob räknade till att de tog 400 steg till skolan tillsammans. Hur många steg tog deras pappa till skolan?
Glassbekymmer
Glassbekymmer
Valentina ville köpa en glass, men saknade 7 kronor. Robert ville köpa samma sorts glass, men saknade 1 krona. Då bestämde de sig för att lägga ihop sina pengar, men även då räckte de inte för att köpa en sådan glass. Hur mycket kostar glassen de ville köpa?
Matematik i Genikampen – fjärde och femte avsnittet
Första, andra och tredje avsnittet av Genikampen innehöll en hel del matte, medan avsnitt fyra och fem var mycker mer fysikinriktade. Jag har inte så bra förståelse för fysik, så jag ska försöka framlägga hur jag försökte göra mitt bästa genom att tänka logiskt och matematiskt i tävlingarna. Samt hur man skulle kunna gjort för att prestera ännu bättre!
Avsnitt 4: Robottävlingen
Tävlingen handlade om att sätta sig in i ett drag-and-drop programmeringsspråk för att skriva program som fick en Lego-robot att utföra uppdrag. Man kunde bygga ut roboten med några Lego-bitar för att underlätta uppdragsutförandet.
Det fanns många saker man kunde göra på banan, men lite tid. Det mest tricksiga var att programmet är kopplat till en verklig fysisk händelse, till skillnad från många ”vanliga” datorprogram. Till exempel innebär det att svänging på 90 grader i programmet inte innebar svängning på 90 grader i verkligheten, utan lite mer om roboten precis hade varit i rörelse. Jag antar att det beror på att den har lite rörelseenergi/intertia/eller vad det heter. Vi fick exempel på hur dessa värden kunde motsvara de verkliga, men inte riktigt någon formel, så det handlade om att prova sig fram helt enkelt, som i många andra tävlingar. Tyvärr fick man bara två försök på själva banan.
Om det inte var trivialt att anpassa speglar från avsnitt 2, där vinklarna faktiskt var mer eller mindre exakta, så var det otroligt mycket svårare här; oexaktheterna ställde till det.
Därför lyckades båda lagen bäst med det enklaste programmet, som körde roboten fram och sedan tillbaka. Jag tror att tävlingen hade blivit roligare, ifall man inte hade fått dubbla poäng för att köra tillbaka roboten. Då skulle man ha vågat sig på någon svårare bana tror jag, och det laget som hade kommit längst i sina eskapader skulle ha vunnit.
Men alla snitsiga planer och programmeringskunskaper hjälper inte, när man inte ens kan stoppa in USB:n på rätt sätt för att det nya programmet ska laddas över till roboten :)
Hur som helst hade det gula laget kommit längre med sitt projekt, så det var en välförtjänt vinst. Men det hade varit spännande att se hur det skulle ha gått till ifall vi ”genier” hade fått öva på Lego-programmering innan. Annars var det lite som att vi skulle ha slängts i vatten i våtdräkter och behövt dyka utan att ha provat på det först!
Avsnitt 4: Bron
I den här tävlingen gällde det att vara stabil! De vinnande taktikerna gick ut dels på att två personer på bron samtidigt stabiliserar varandra och dels på att två plankor under en person stabiliserar personen bättre.
Så hur ska man såga i plankorna? För rakar rep är svaret självklart: såga skårorna på samma avstånd som repen är! För korsade rep är det lite svårare, det beror på var man fick ha plankan! Jag tror att Johan vill ha en kort planka en tredje del in (dvs förhållandet mellan avståndet bryggkant-planka skulle vara dubbelt så stort som planka-kryss). Då skulle avståndet mellan skårorna på grund av likformighet vara en tredje del av avståndet mellan repen. Vi hade ingen linjal eller måttband, men vi visste dessa avstånd. Därför kunde vi på ett ungefär räkna ut (med halveringsmetoden) var man skulle göra skårorna. Vinkeln gissade vi på :) Och det funkade!

Avsnitt 4: Pusselduellen
Svårt att skriva om en tävling som man inte fick testa på! Den första pyramidpusslet hade jag sett förut, den är icke-trivial! Ett sätt att lösa det på är att få till en bit att ligga med ”rätt” vinkel, dvs en vinkel som känns vettig med tanke på slutresultatet. Då blir det tämligen rätt att fylla i slutresultatet, med tanke på att pusslet dessutom är spegelsymmetriskt.
Angående andra pusslet säger Theres att det är fyra likadana bitar. Det är lite svårt att se på videon, men jag tycker att de bara nästan är likadana. Det underlättar enormt om bitar är exakt likadana: Då vet man att en sådan bit måste innhålla översta kulan t.ex. och så börjar man testa sätt som den biten kan ligga på. Man ser också att Theresa behövde bygga ihop bitarna ”alla samtidigt”, det gick inte att sätta in dem en i taget. Detta är något av det svåraste att komma i pussel. Lättare pussel, liksom matteproblem, löses ett steg i taget (och man förstår vilka steg det är som ska tas). I de svårare måste man däremot komma på en följd av steg som löser det, vilket i mitt tycke är exponentiellt mycket svårare!

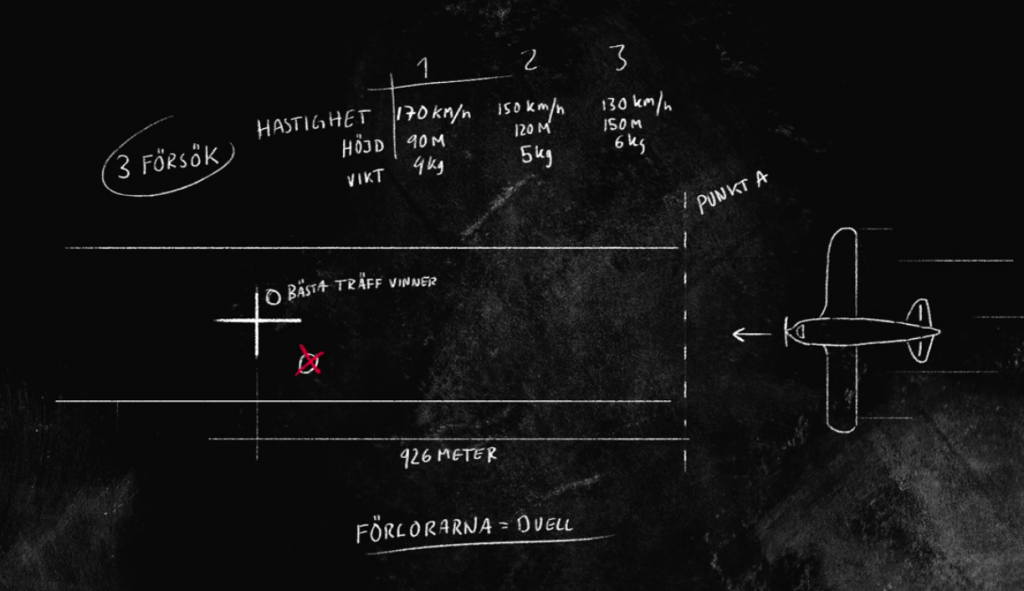
Avsnitt 5: Flygplansbomben
I flygplanstävlingen skulle vi räkna ut tiden att släppa en kalkbomb på för att den skulle åka ett visst avstånde. Så som Axel säger är det en vanlig uppgift från fysikböcker. Vad händer då när ”genier” ska räkna på det på riktigt?
Msn sätter upp en modell, som tar hänsyn till hastighet och acceleration och sätter in de kända värden. Varför blir det så fel? Dels är luftmotståndet tydligen svår att beräkna exakt, men dels tror jag det skedde missförstånd. Vi fick planets hastighet relativt marken trodde vi, men det var nog relativt luften. Det borde vi kanske ha insett när det blev så mycket fel, men jag hade ingen intuition för fysik, så tyckte inte det var så värst dåligt resultat att hamna 65 m bakom. Hade jag gjort det själv skulle det inte gått lika bra tror jag! Jag skulle iofs använt en enklare modell.
Poängen är att om modellen inte fungerar perfekt handlar inte om att hitta en bättre modell snabbt, utan att modifiera svaren utefter hur fel de var. Detta är precis vad gula laget gjorde och de vann på det! Fredrik lade fram ett hypotetiskt värde genom att ställa upp ett linjärt samband ”x sekunder = y meter”. Det var lite tur att det fungerade, men det var ju helt rätt tänkt tänkt. Det berodde på att hastigheterna på planet ökade linjärt (170 km/h – 150 km/h – 130 km/h) och samma sak gällde höjden (och vikten). Allt som allt tror jag det borde blir ett linjärt samband för tid-avstånd också, i alla fall för små förändringar. Kul att det fungerade!
Avsnitt 5: Tryckluftkanoner
Jag kunde i stort sett ingenting om tryck när jag gick in i tävlingen, men efteråt berättade Axel om hur man modellerar skottkurvan utefter tryck och storlek och sådär. Vi räknade ut lite vinklar efteråt i lugn och ro, det var roligt!
När det gällde att komma på vinklar snabbt och bygga finns det ingen tid för räkning tyvärr. Det handlar mer om praktiska erfarenheter och tänk (hur fixar man läckande kanon). Där är en matematisk hjärna till ingen nytta!
Övningen med vattenmelonerna kunde man däremot tänka lite på. Fredrik har återigen rätt i att om uppgiften ska lösas med empiri så är det bara en parameter i taget som man tjänar på att ändra på.
Hur kunde man räkna ut den ungefärliga vinkeln? Jag gjorde det genom att rita en triangel på tavlan som var likformig med vår skjutbana (vi antog att kanonen skulle skjuta rakt uppåt om vi hade maximalt lufttryck) och sedan lägga på likadana vinklar (egentligen fördubbla dem) tills det skulle bli 90. Sedan kan man gå baklänges och räkna ut den ursprungliga vinkeln. Då fick vi 10.
I verkligheten beter sig inte saker perfekt, alltså inte som i modellen. Kanonen skjuter inte rakt uppåt och inte rakt framåt heller för den delen (som man ser blev det fler skott till vänster om målet än till höger). Återigen löser man uppgiften bäst genom att titta på det som faktiskt hände (här var referensskottet jätteviktigt att tänka på) och sedan anpassa sina värden därefter. Modeller är bra när man inte har någon aning, men har man något att utgå ifrån så borde man göra just det. Ännu än vinst för empiri!
Avsnitt 5: Stavningsduell
Inte särskilt mycket matte här, men bra att hålla reda på en regel för att skilja på enkelbokstav och dubbelbokstav. Överensstämma = överens + stämma (haha, lite matte blev det ändå), så det ska vara två ”s”. Kom dock ihåg att det kan aldrig bli tre ”s” (eller någon annan bokstav för den delen), utan de förkortast alltid till två i svenskan. Exempel: tuggummi = tugg + gummi.
Matematik i Genikampen – kluringar från tredje avsnittet
Det tredje avsnittet av Genikampen var sprängfyllt med matte! Det var så pass mycket matte att jag behöver dela upp inlägget om det i två delar. I första delen vill jag presentera problemen som ingick i den andra lagtävlingen, samt lösningar till de alla.
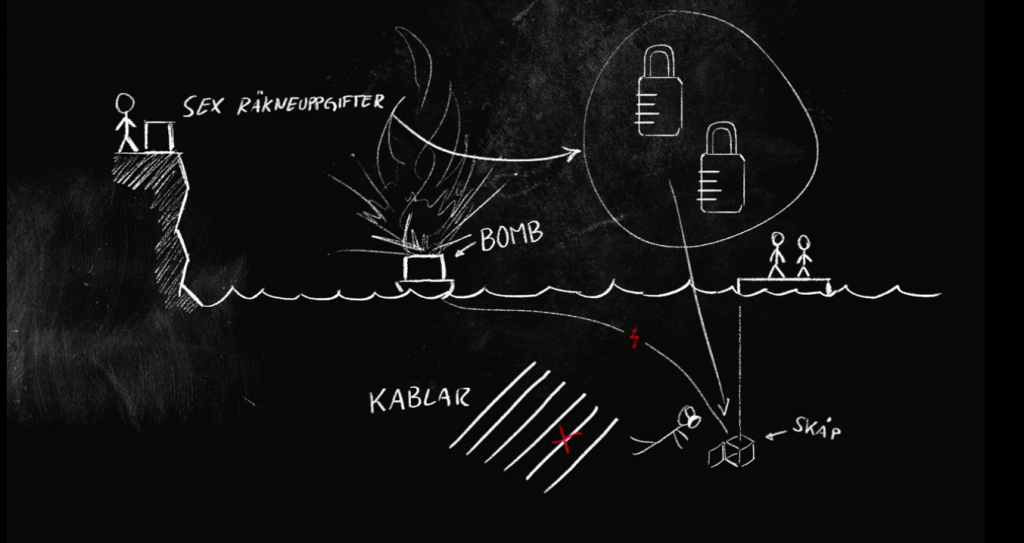
Kodlås 1 bestod av tre uppgifter, där varje uppgift gav en siffra. Den tresiffriga koden skulle låsa upp det första låset under vatten.
Kodlås 2 gav på samma sätt ett tresiffrigt kod till andra låset.
Kablar 5 uppgifter gav 5 siffersvar, där 0 stod för A, 1 stod för B och så vidare till 9 som stod för J. Bokstäverna var kopplade till kablar som var safe att klippa av.
Kodlås 1
sifferkod 1
Sofie och Maria är syskon. För deras åldrar gäller följande samband: Summan är lika stor som produkten. Hur gamla är Sofia och Maria?
Addera talen.
Det här var enda uppgiften vi först gjorde fel på!
Den går ut på lista ut åldrarna S och M sådana att S+M = S·M.
Ekvationen S·M − S − M = 0 beskriver en hyperbel, som har oändligt många punkter. Men eftersom vi frågas efter heltalslösningar (och det bara ska vara en lösning som funkar), så funkar det bra att gissa.
Vi gissade på 0+0 = 0·0, men 2+2 = 2·2 funkar också. Det senare betraktas troligare som ålder (kanske säger man aldrig att någon är 0 år gammal), så svaret var 4 (och inte 0 som vi först trodde).
Första kodlåssiffran är 4.
sifferkod 2
En tjuv stal en säck med guldmynt i ett slott. För att komma ut ur slottet måste han passera tre vakter. Den första mutade han genom att ge vakten hälften av guldmynten. Vakten gav dock tillbaka 100 guldmynt av ren medkänsla. Den andra vakten fick hälften av tjuvens pengar men gav sedan tillbaka 50 guldmynt. Den tredje vakten fick hälften av pengarna men gav sedan tillbaka 25 guldmynt. Tjuven hade då 100 guldmynt kvar. Hur många mynt hade han från början?
Dividera svaret med 40.
Här är det lättast att gå baklänges. Tjuven hade 100 guldmynt i slutet.
Nu kollar vi hur mycket han hade innan varje händelse:
Innan tredje vakten gav honom 25 mynt hade han alltså 75 mynt (100-25).
Innan tredje vakten fick hälften av pengarna hade tjuven 150 mynt (75*2).
Innan andra vakten gav honom 50 mynt hade han 100 mynt (150-50).
Innan andra vakten gick hälften av pengarna hade han 200 mynt (100*2).
Innan första vakten gav honom 100 mynt hade han 100 mynt (200-100).
Innan första vakten fick hälften av pengarna hade han 200 mynt (100*2).
200/40 = 5.
Andra kodlåssiffran är 5.
sifferkod 3
Ett tåg består av ett lok och fem vagnar (A, B, C, D och E). På hur många sätt kan vagnarna ordnas så att vagn A kommer närmare loket än vagn B kommer?
Dividera svaret med antalet konsonanter i det svenska alfabetet.
Det går att ställa vagnarna på rad på 5! sätt. 5! står för uttrycket 5*4*3*2*1 = 120.
Detta beror på att en av de fem vagnarna kan ställas längst fram, en av de fyra kvarstående kan ställas på andra plats, en av de tre kvarstående på tredje plats, en av de två som är kvar kan ställas näst sist och ett alternativ har vi kvar för den vagnen som ska stå sist.
Exakt hälften av de ordningarna är sådana att A kommer närmare loket än B (och exakt hälften är tvärtom). Det beror på att alla ordningar kan paras ihop: varje ordning är i par med nästan samma ordning, fast där A och B har bytt plats. Till exempel är CADEB i par med CBDEA. Därför ska vi dela svaret med 2.
(Det här är för övrigt i stort sett samma uppgift som 2(a) här: LÄNK http://mattebloggen.com/wp-content/uploads/2014/09/Lektion2Permutationer.pdf)
120 / 2 = 60.
I det svenska alfabetet finns det 20 konsonanter (29 bokstäver totalt, varav 9 är vokaler).
60 / 20 = 3.
Tredje kodlåssiffran är 3.
Kodlås 2
sifferkod 1
Sofie satt på balkongen och gjorde sin matteläxa. Hon hade just skrivit svaret på en uppgift, när en duva kom flygande och lämnade sitt ”visitkort”, så att sista siffran (= entals siffran) i svaret inte syntes. Skillnaden mellan det ursprungliga svaret och det svar som nu syntes var 276. Vilket var det ursprungliga svaret?
Addera svarets siffror.
Om det ursprungliga slutsiffra var A, så kan talet skrivas som 10*X + A (oavsett hur många siffror talet har kan de skrivas som ett visst antal tiotal plus en slutsiffra).
När duvan har varit framme och busat hade Sofie talet X framme (antalet tiotal i det ursprungliga talet).
Det betyder att 10*X + A – X = 276
Det vill säga 9*X + A = 276.
Talet 276 är inte med i nians tabell, utan ger rest 6 när man dividerar med 9. Det betyder att A måste ha varit 6 och X i sin tur måste ha varit 30 (=270/9).
Så talet som stod där från början var 306 (=10*30+6). Detta är det enda svaret.
3+0+6 = 9
Första kodlåssiffran är 9.
sifferkod 2
Tre positiva heltal (naturliga tal) är så beskaffade, att om vart och ett multipliceras med de två övrigas summa, får man produkterna 120, 133 och 169. Bestäm talen.
Addera dessa tre tal och subtrahera det med det tal som kommer efter 13 i Fibonaccis talföljd.
Vi har tre tal som vi kan beteckna med a, b och c. Då vet vi att:
a*(b+c) = 120
b*(a+c) = 133
c*(a+b) = 169
Sen ska man bestämma talen står det, men det struntade vi i! Man skulle nämligen addera dessa tre tal senare, så vi fokuserade på att bestämma a+b+c (så man behöver inte bestämma vart och ett av talen).
c*(a+b) = 169. Eftersom 13*13 = 169 och 13 är ett primtal, går det bara skriva 169 som en produkt av tåv positiva heltal på två sätt:
169 = 13*13
169 = 1*169.
I det första fallet får vi att a+b+c = 13+13 = 26
I det andra fallet får vi att a+b+c = 1+169 = 170
Resan nu inser man att det är det första som är rätt (eftersom vi ska subtrahera 21 och få en siffra, men vi bevisar det korrekta svaret ändå utan att använda det).
133 = 7*19 och 7 och 19 är primtal, därav a+b+c är antingen 7+19=26 eller 1+133=134, så det måste vara 26!
(Detta stämmer även med faktoriseringen av 120 = 20*6 till exempel. Nu kan vi bestämma a, b och c för sig men det är för mycket jobb).
Fibonaccis talföljd är 1,1,2,3,5,8,13,21,34 och så vidare. Varje tal från och med det tredje är lika med summan av de två talen innan. Läs coola grejer om Fibonaccitalen
26 – 21 = 5
Andra kodlåssiffran är 5.
sifferkod 3
((√256 x 20 − 252 + 152 + 34) x 10) / 5 =
Det här är bara en vanlig uträkning. Men man kan ändå räkna ut det lite smart:
Då 256 är 2 upphöjt till 8, så är roten ur det 2 upphöjt till 4, det vill säga 16.
Multiplicerar man den stora parentesen med 10 och sedan dividerar med 5, så är det samma sak som att multiplicera parentesen med 2.
Sedan räknar man ut potenserna.
Då får man följande uttryck och du kan följa lite hur man kan tänka för att räkna snabbare:
(16*20 – 625 + 225 + 81)*2 =
(320 + 225 + 81 – 625)*2 =
(320 + 306 – 625)*2 =
(26 – 25)*2 =
1*2 = 2
Tredje kodlåssiffran är 2.
Kablar
Kabel 1
(6y-7)/4 + (3y-5)/7 = (5y+78)/28
Vad är y?
Detta är en vanlig ekvation, dessutom ser man att 28 är en minsta gemensam multipeln till 4 och 7, så det lättaste är att få bråken till gemensam nämnare:
7*(6y-7)/28 + 4*(3y-5)/28 = (5y+78)/28
Nu kan vi glömma bort 28:
7*(6y-7) + 4*(3y-5) = (5y+78)
Multiplicerar in talen:
42y – 49 + 12y – 20 = 5y + 78
Förenklar:
42y + 12y – 5y = 78 + 49 + 20
49y = 147
7y = 21
y = 3
Första kabeln ska ha bokstaven (3=)D.
Kabel 2
I herrtruppen till VM i cykel hade lagledare Hjulström tagit ut cyklister från enbart två klubbar – lika många från varje klubb. När det var dags för lagtempo, visade ett testlopp att alla åkarna i stort sett var jämngoda.
Hjulström beslöt därför att ta med två cyklister från vardera klubb i lagtempolaget. Ändå gav detta inte mindre än 36 tänkbara lagsammansättningar! Hur många cyklister bestod truppen av?
Den här uppgiften var inte det lättaste att tolka, så vi försökte tolka på ett sätt som skulle ge ett ensiffrigt svar.
Vi vet att det finns n cyklister i var och en av de två klubbarna. Om man ska räkna hur många sätt det finns att välja två stycken ur en klubb får man det från uttrycket n*(n-1)/2 (n sätt att välja den första, n-1 sätt att välja den andra, dela med två för att ordningen på de inte spelar roll, precis samma idé som i vagnuppgiften).
För att få antalet sätt att sätta ihop laget måste man multiplicera sätten att välja två från första klubben och två från andra klubben, vilket ska ge 36. Då n är densamma för båda klubbarna, innebär det att det ska finnas 6 sätt att välja två pers från en av klubbarna (för att 6*6=36).
Nu får vi uppställningen n*(n-1)/2 = 6, vilket betyder att n*(n-1)=12, så n måste vara lika med 4.
Så då är frågan om vi ska svara 8 eller 4. Troligen 8 eftersom det verkar som att man räknar in båda klubbarna i truppen.
Andra kabeln ska ha bokstaven (8=)I
Kabel 3
(15 – 7)(1500 – 25) – 2200 x 3 – 84 – 210 – 79 =
En vanlig uträkning till! Tur att man kan sina tvåpotenser:
210 = 1024
84 = (23)4 = 212 = 4096
(15 – 7)(1500 – 25) – 2200 x 3 – 84 – 210 – 79 =
8*1475 – 6600 – 4096 – 1024 – 79
Egentligen kan man bryta ut 8:an på tre ställen för att slippa räkna en stor multiplikation:
8*1475 – 8*825 – 8*512 – 8*128 – 79 =
= 8*(1475 – 825 – 512 – 128) – 79 =
= 8*(650 – 512 – 128) – 79 =
= 8*(138 – 128) – 79 =
= 8*10 – 79 =
= 80 – 79 =
= 1
Tredje kabeln ska ha bokstaven (1=)B
Kabel 4
Lille Micke sålde två fotbollskort för 21 kronor.
På det ena kortet tjänade han 10 % och på det andra kortet förlorade han 10 %.
Allt som allt tjänade han 5 %. Hur mycket hade varje fotbollskort kostat i inköp?
Svar: Addera dessa två tal och dividera summan med
den fjärde decimalen i pi.
Ett av de (till synes) svårare problemen! Lätt att virra ihop sig med procent. Men precis som i kodlåsproblemet med primtal behöver man inte lösa hela uppgiften. Vi ska ju använda summan av ursprungspriserna sedan, därför behöver vi egentligen inte ta reda på vart och ett av priserna, utan på vad det var tillsammans.
Om korten hade kostat A och B från början kan vi skriva villkoren som
21 = 1,1*A + 0,9*B = 1,05*(A + B).
Men om det är A+B vi är ute efter är uppgiftens andra rad helt onödig! Vi har:
21 = 1,05*(A + B)
A + B = 21/1,05 = 2100/105 = 300/15 = 100/5 = 20.
Och tur att man kan lite pidecimaler! 3,14159… Så svaret ska divideras med 5. 20/5 = 4.
Fjärde kabeln ska ha bokstaven (4=)E
Kabel 5
Då ett visst fyrsiffrigt tal multipliceras med fyra, får man ett nytt fyrsiffrigt
tal, där sifferföljden är omvänd jämfört med det första talet,
dvs. 4*ABCD = DCBA
Vilket är det ursprungliga talet?
Subtrahera svaret med 2004 och dividera den summan
med det tionde primtalet.
Här berättar jag en stor del av lösningen i tv. Men nu har jag chansen att kortfatta lösningen.
A = 1 eller 2, annars blir inte talet DCBA fyrsiffrigt. Då HL är jämnt, måste A = 2.
Då är D = 8 eller 9, annars är HL för litet (VL är minst 4*2000). Då 4*D ska sluta på A måste D = 8.
Vi har då 4*2BC8 = 8CB2.
Om vi fortsätter uträkningen med tiotal måste 4*C + 3 sluta på B. Samtidigt får inte B vara för stort (måste vara mindre än 3) för att multiplikationen 4*B00 inte ska ge ett till tusental.
Vi testar med olika C (i uppgiften är det inte givet att siffrorna A,B,C och D är olika även om det brukar vara så i sådana rebusar):
4*C + 3 = (”slutar på”) B
4*0 + 3 = 3 – för stort
4*1 + 3 = 7 – för stort
4*2 + 3 = 1
4*3 + 3 = 5 – för stort
4*4 + 3 = 9 – för stort
4*5 + 3 = 3 – för stort
4*6 + 3 = 7 – för stort
4*7 + 3 = 1 –
4*8 + 3 = 5 – för stort
4*9 + 3 = 9 – för stort
Då vet vi att B måste vara 1 och C är antingen 2 eller 7. Vi testar med båda:
4*2128 = 8512 – passar inte.
4*2178 = 8712 – passar!
Nu räknar vi ut kabelbokstaven:
2178 – 2004 = 174
Tur att man kan lite primtal: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31…
Det tionde primtalet är alltså 29.
174/29 = 6 (egentligen hade man kunnat gå från slutet och testat de tio olika ursprungstalen 2004+0, 2004+29, 2004+29*2 och så vidare, men det är lätt att vara efterklok).
Fjärde kabeln ska ha bokstaven (6=)G
Vi var klara med uppgifterna lite innan motståndarbomben smällde (men höll på att kontrollräkna)!
Gillade du för övrigt sifferrebusen, kan du kolla upp några lite svårare här på bloggen: Granrebus, Sifferrebus, Palindromrebus och Trigonometrisk rebus.
Matematik i Genikampen – andra avsnittet
Andra avsnittet innehöll kanske inte lika mycket matte som första avsnittet, men det betyder ju inte att man inte skulle vara smart för att klara tävlingarna. Och allt som har med kreativt tänkande att göra kan jag om jag vill koppla ihop med matte så nu tänker jag göra det.
Flottbygge: Planering och materielinköp
Vi fick 3000 kronor för att handla materiel till vår flotte. Tävlingsledarna skulle kopiera både gula och blå lagets inköp och lagen skulle få de andras inköpta material först. Men i andra omgången skulle lagen få eget material, så det gällde att inte köpa sjukt dåliga saker. Framförallt gällde det att köpa något som man själv skulle ha mer nytta av än motståndaren i samma situation.
Enligt tävlingsreglerna behövde man antingen vinna båda omgångarna för att vinna hela tävlingen eller vinna en av omgångarna med bäst vinsttid (det vill säga, bara tiden för den vinnande omgången räknades). En grej som är lätt att se i efterhand och lite svårare att tänka på innan tävlingen är att det är bara den andra omgången som spelar roll. Givet erfarenhet och att man bygger med eget material tar den andra omgången med störst sannolikhet kortare tid för båda lagen. Det gällde alltså att samla erfarenhet i första och ge järnet i andra omgången.
Under tidspress kunde vi inte vara så värst smarta och planerade en konstruktion som skulle bli alldeles för tidskrävande i andra omgången (så den övergavs). Inne i affären fokuserade vi på att göra beräkningar av typen ”hur mycket volym måste flotten ha för att bära allas vikt?” (blå laget räknade detsamma verkar det som). Fysik i all ära, men ingenjörskonsten med höftning snarare än exakta beräkningar tar ändå alltid priset när det är snabba puckar och inte forskning som gäller.
Andra beräkningar som vi kunde göra skulle då vara hur många hinkar sand flotten skulle kunna bära (förutom oss själva då). Jag kom tyvärr inte ihåg att vi hade fått hinkmått eller mått på lådan vi skulle fylla också, så jag fokuserade på att räkna på kostnaden istället. Tog lite i överkant på varje vara för att inte hamna över (samt för att räkna snabbt) och det slutade med att vi verkligen inte hamnade i överkant, utan hade kunnat köpa typ ett halv toasits till.

Att köpa toasitsar som åror var en briljant idé utav Nina som sparade gula laget mycket tid som annars skulle behövs till åror-tillverkning. Synd att de var så dyra!
Flottbygge: Första omgången
Första omgången gick för båda lagen ut på att samla erfarenhet, framför allt om en bra form på flotten samt om hur många omgångar fram och tillbaka som skulle behövas för att fylla lådan med sand. Vi hade nio hinkar tillgängliga, om jag minns rätt (dock sänkte vi i gula laget en hink i sjön i första omgången). Gula laget hann dumpa sand två gånger, medan blå fyllde hinken på tre gånger! Det betydde att två eller tre gånger skulle behövas i andra omgånger för att vinna hela tävlingen.

Om man skulle åka två omgångar långsamt istället för tre snabbt skulle man ändå vinna tävlingen då tiden att åka fram-tillbaka-fram är tre intervall, medan fram-tillbaka-fram-tillbaka-fram är fem intervall, alltså tar det andra fallet mer än 50% mer tid än det första, om man nu åker med samma hastighet. Tiden det tar att dumpa sand är försumbart i jämförelse med tiden det tar att åka. I programmet hör man att vinsttiden är mer än femtio minuter. Skulle gissa på att max 15 min gick ut på att bygga för blå laget, medan allt annat var rodd (i snitt 7 min per sträcka fram eller tillbaka).
Flottbygge: Andra omgången
Vi i gula laget satsade på att fylla lådan på två rundor, det vill säga åka fram-tillbaka-fram och vinna. Blå laget satsade på samma sak. Viktiga skillnaden för gula laget var att istället för att lägga de 12 frigolitbitarna i fyra lager lägga dem i tre lager. Det betyder att flotten blev till ytan större (4 plattor iställer för 3) och mer stabil (lägre). Det var helt klart den största förbättringen för gula laget gentemot första omgången. En eloge till blå laget som körde på den utformningen av talet 12 redan från omgång ett! I slutändan som det syns i avsnittet var det inställning och småsaker som avgjorde och inte matten. Men utan de idéer som jag nämnt skulle det gula laget varit körda. Tur att det är hög lägstanivå på lagen, så att det inte blir jätteskämmigt när vi spelar genier!
Laser och speglar
Andra tävlingen gick ut på att rikta en laserstråle med hjälp av speglar. Strålen skulle förbi en massa hinder och träffa en ”prisma” (jag tyckte det mera såg ut som en halvklot ihopsatt med en halvikosaeder eller nåt, en prisma ska ha två kongruenta parallella sidor vad jag vet). Tävlingen gick i omgångar; varje omgång bestod av en planeringsfas och en resultatfas. Under planeringen fick man mäta på banan, ställa om och flytta på speglar, göra eventuella beräkningar. Sedan fick man se laserstrålen tändas och en person fick springa fram och göra högst en markering på banan.
Detta syns inte i tv men tävlingen tog hela 14 (!) omgångar. Första omgången träffade gula laget sin första spegel, medan blå laget gjorde inte ens det. Till andra omgången flyttade vi i andra laget andra spegeln lite för att strålen skulle träffa den, men tydligen flyttade vi den lite för mycket! Det var bara på tredje omgången som andra spegeln blev träffad. Och detta var bara speglarna i början, som sattes ut på samma höjd allihopa och med enklar vinklar på 45 grader. Om det var så små marginaler på dem skulle spegelinställningarna i tre dimensioner bli exponentiellt mycket svårare!
Vilket de också blev. Beräkningarna kunde man kasta i papperskorgen och vårt lags strategi var att köra på empiri, det vill säga testa och sedan göra små ändringar. Sedan kan man göra empiri olika bra ocskå. Säg att du ska gissa ett tal mellan 1 och 100 och får veta om din gissning är mindre eller större än det korrekta talet. Då är det bäst att fråga om talet 50 (eller 51). Om det tänkta talet är större, frågar du om 75 och så vidare. På liknande sätt var det för oss när vi ställde in spegelvinklar (både plattformens vinklar och spegelns vinkling): Börja med en gissning, gå sedan ganska långt åt andra hållet (för att definiera en gissningsintervall), sedan någonstans i mitten om man ser att den korrekta vinkeln är mellan de två gissningar, sedan fokusera på rätt halva av intervallet för att få rätt fjärdedel och så vidare.
Detta funkar bra med småvinkeländringar, eftersom, som jag säger i programmet, ”sinus är linjär vid 0”. Det kommer från att
.
Och då även
.
Om markavståndet (dvs avståndet projicerat ovanifrån) från spegelns mittpunkt till nästa spegel är given, så kommer alltså vinkeln bero linjärt på avståndet i den andra ledden (just det vi försöker gissa). Dubblas vinkeln, så dubblas avståndet alltså.
Så för små vinklar funkar det då med samma genomsökningsstrategi som med talen från 1 till 100. T.ex. testar vi med 5-graders vinkeln, sedan med 7 och om strålen ska vara däremellan testar vi med 6 grader (istället för att vara smarta och försöka beräkna att vi ”borde” testa 6,5 eller nåt sånt). Sånt kan ”inte ens jag” beräkna snabbt utan miniräknare och dessutom är det massa felmarginaler på mätningar, så det hade varit meningslöst ändå.
Vi fick instruktioner om att skriva lite smarta saker på tavlan, speciellt under första omgången. Det finns inte jättemycket att skriva när man kör på empiri annat än små anteckningar, så vi roade oss lite istället:
Så klart fanns det annat att tänka på än att bara höfta och ändra inställningar. En viktig sak är hur många speglar man bestämde sig för att använda (man behövde inte använda alla). Ju färre speglar, desto färre lyckade steg man behövde göra. Men å andra sidan skulle varje steg vara något svårare om man skulle försöka ställa in speglarna i 3D (vi kunde ju inte ställa de var som helst, utan bara på några av hindren). Vi körde på strategin ”better be safe than sorry” och jag blå laget gjorde det också, det vill säga använda många speglar med mindre avstånd/svårighetsgrad mellan varje intilliggande par.
En annan sak som jag kom på och var ganska stolt över var att använda flera av de lediga speglarna att ställa på rad för att chansa på att strålen skulle råka träffa nästa spegel också. Lasern bana var mycket värdefull att se och får man se ett steg till ”gratis” var det mycket värt.
Blå laget körde på att titta i speglarna och försöka se prisman i första spegeln. I programmet är jag skeptisk till hur de kunde låta ögat vara så stabilt, men det funkade ju hyfsat bra för dem. Så kanske är det en hållbar strategi ändå! Problemet är att med många speglar multipliceras felet för varje steg. Tänk på när du är i ett rum med massa speglar. Om du flyttar ögat, flyttar de mer avlägsna spegelbilderna mycket snabbare!
Svår tävling var det och krävde mycket tid och energi. Men det var nog min favorittävling i hela Genikampen. Jag gillar att lösa problem när man har ganska god tid på sig. För varje steg fram man kommer får man en kick och vill fortsätta. Dessutom kan man komma på fler och fler strategier som kan testa och föra en fram bättre och snabbare!

Pentago
Duellen gick ut på att spela några omgångar av spelet Pentago, bäst av tre. Duellanterna fick veta reglerna lite innan och provspela ett par gånger. Det finns ju stor risk för missuppfattning, även när man kommunicerar med oss genier ;) Det vore tråkigt om någon gjorde ett olagligt drag i tv eller nåt, även om det såklart svårt att göra det i just det här spelet.
Som i många spel med ett litet spelplan finns det redan beräknat hur man ska spela optimalt. I det här fallet har första spelaren en vinnande strategi, detta behövde dock beräknas med hjälp av en superdator! I massa andra sådana spel är det bevisat att första spelaren har i alla fall en icke-förlorande strategi, som t.ex. i schack (vit kan aldrig förlora om hen gör rätt!) i ”fem i rad” på ett oändligt bräde, men i många sådana spel finns det så många möjligheter att man inte har räknat ut den konkreta strategin. Pentago är rätt litet så det går att beräkna.
Testa att spela och vinna Pentago
Frågan är om man kan lära sig den vinnande strategin utantill, det har jag ju inte försökt mig på. Även om datorn kan göra det på några sekunder, kanske kan det ta en människa veckor för att ”plugga öppningar”. Det hade inte duellanterna. De hade kunnat fokusera på att plugga hur man ”inte gör fel”, t.ex. att man inte ska lägga i hörnen som första spelare och hur man i så fall ska svara som andra spelare. Men jag tror inte det skulle ha hjälpt för att garanterat vinna. Jag tror man kan jämföra Pentago med Othello: Det tar ett tag att bemästra och att lära sig se mönster, men när man väl gjort det så kan man spöa vilken nybörjare som helst. Det var skönt att duellanterna inte hade spelat spelet förut, så att de tävlade på samma villkor.
Jag och Axel fick senare låna spelet och vi försökte komma fram till en vinnande strategi ”för hand” genom att testa olika möjligheter, men jag tror inte vi hann göra det på en halvtimme :)
Matematik i Genikampen – första avsnittet
I höst är jag en av deltagarna i SVT:s program Genikampen. Programmet går i åtta avsnitt och jag tänkte beskriva händelserna i avsnitten ur ett matematiskt perspektiv.
Själv är jag matteintresserad och har övat mycket i problemlösning. Jag tror att detta har gjort mig smart på flera sätt, inte bara bra i huvudräkning. Matte för mig är så mycket mer än att räkna och därför vill jag visa nedan hur man kan tänka på ett matematiskt sätt även när man inte ”räknar”. Matte för mig handlar om att tänka.

Orientering på sträcka
Tävling ett börjar med att vi blir uppdelade i lag med 6 personer i varje. Uppgiften är att orientera i skogen, det vill säga passera 4 kontrollpunkter innan man kommer fram till målet. Laget får en karta, men ingen kompass. Det gäller att göra detta inte på kortast tid, utan på kortast sträcka! Två personer i laget har GPS-sändare, som sträckan mäts på, men även de andra 4 personerna i laget ska hålla ihop med personerna med GPS, ingen får ”scouta” framme. (Överlag fick deltagarna veta reglerna i detalj och även fick ställa förtydligande frågor, vilket inte visas i tv.)
Jag antar att man tar medelvärdet av de två GPS-positionerna för att få fram banan för att sedan mäta avståndet. Vi fick veta att om avståndet skiljde sig med mindre än 50 m, så var det tiden som gällde. 50 m var så pass lite i sammanhanget (man gick kanske i 35 minuter), så det rätta valet var att strunta totalt i tiden och fokusera på att gå precis kortast.
Hur hjälper matten här då? Jo, man bestämmer att personerna med GPS-sändarna måste gå så rakt som möjlig (DUH!). Detta löser man genom att de inte går först, utan i mitten eller sist. Då kan de personerna som går först gå lite fel (och på så vis ”scouta”). Om personerna som går först går längs med kateterna i en rätvinklig likbent triangel med kateterna 3 m, så kommer personen med GPS:en gå ”bara”
4,24 m istället för 6 m alltså! En vinst på 1,76 m! Sker detta 100 ggr, vilket var rimligt för banan, så vinner man redan 176 m på att gå så. Pythagoras sats ftw!
Givetvis är detta egentligen en försumbar optimering i jämförelse med att ”gå rätt”, vilket sätter orienteringsskills över matten i det här fallet. Så är det ibland, men lite bidrag från olika sätt att tänka här och var är sånt som avgör tävlingarna.

Orientering på tid
Andra delen av första tävlingen gick ut på att orientera på ett fabriksområde och hitta halvgömda kontoller. I kontrollerna fanns ledtrådar, mer om dem senare. Här hade gula laget 3 minuters försprång, vilket visade sig inte bara hjälpa, utan stjälpa.
Det fanns nämligen i princip två optimala sätt att ta kontroller (med kortast sträcka): medurs eller moturs (ordningen för kontrollerna blev ganska naturlig), eftersom man skulle tillbaka till samma ställe. Gula laget började, men eftersom blåa laget följde samma riktning, kunde de spara tid på att inte leta efter kontroller, utan observera det gula laget när de var precis ikapp, men lite efter. Det hade blivit annorlunda ifall det blåa laget hade valt motsatt riktning, då skulle förmodligen inget lag få fördel (eller i alla fall är den förväntade fördelen lika) av att vara ”efter”. Banorna skulle korsa varandra i ungefär mitten och då skulle det blivit mer ”rättvisst”. Lite kul ändå att slumpen påverkar!
Uträkningar
Sista delen av första tävlingen gick ut på att göra uträkningar (Genikampen kallar det ”lösa ekvationer”, men jag håller inte med om den termen, eftersom ”ekvationer” för mig förutsätter ett närvaro av ett ”lika med”-tecken och någonting okänt.) Om uppgifterna görs i fel ordning (det vill säga, man försöker få ett resultat utan att veta att KATT = 2 och HARE = 5), så kan man inte få ett svar, men man kan förenkla uttrycken. Gula laget öppnade just ett uttryck med okända först (och visste ju inte vad som väntade), så det enda som fanns i början var att förenkla, vilket gjorde att man kunde räkna ut resultatet av det uttrycket snabbare efteråt.
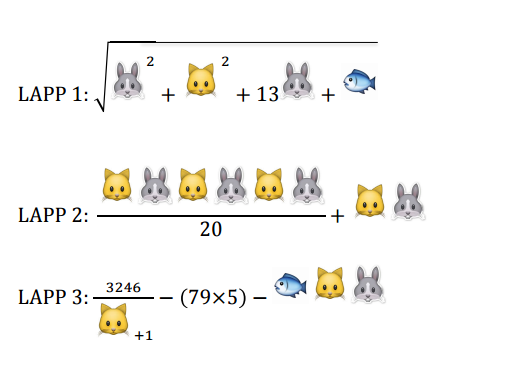
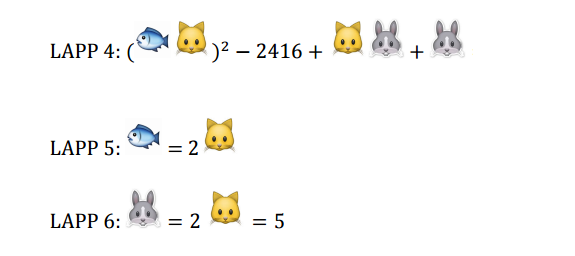
Som sagt, beräkningar är inte allt som matte är. Nu råkar jag vara snabb på att göra aritmetiska beräkningar, men kanske hälften av de verksamma matematiker jag träffar är inte bra på snabba beräkningar alls. Det är lite som att vara bra på Rubiks kub: Man har antingen lärt sig det eller inte. Man kan vara smart på knep & knåp utan att vara bra på Rubiks kub. Jag skulle inte heller säga att de som är bra på huvudräkning är automatiskt bra på matte, även om man förmodligen är bra på att se mönster, vilket hjälper en att räkna snabbare. Överlag, de som är bra på räkning är personer som är så pass lata att de vill göra det snabbt :)
Testa dig själv på tid om du tycker att det är kul att räkna.
Paintball-quiz
Andra tävlingen gick ut på att ha paintball-dueller med frågesport. Inte jättemycket matte, men man kan fundera över taktiken matematiskt. Det gäller att bedöma sina chanser att träffa vid skjutningen samt chanser att svara rätt på frågan. Om du inte är säker alls på att träffa (t.ex. Valentina som aldrig har sjutit/träffat i sitt liv) bör du skjuta snabbt om det är liten sannolikhet om din motståndare träffar. Med stor sannolikhet missar båda och då har du i alla fall första tjing på frågan. Men det kan också vara dumt att svara först om du t.ex. funderar mellan två alternativ: Då kan det vara bra att motståndaren eventuellt kan utesluta ett av alternativen genom att svara fel. Men den situationen händer typ aldrig.
Om man däremot är bra på att träffa bör man förmodligen börja med att undvika skottet från motståndaren och sedan skjuta själv i lugn och ro. Detta kan ge en säkra poäng, samt chansen att svara först!
Givetvis kan motståndare av liknande ”typ” träffar varandra, vilket resulterar i symmetrisk strategi och en Nash-jämvikt, men det är inget man hinner tänka på när man står där framme :) Då blir det lite kaotiskt och återigen slumpen som avgör.
Ordbygge
Duellen gick ut på att forma ord. Ser man inte färdiga ord så är det brute force som gäller (dvs testa alla möjligheter: Vilken kub är först, vilken är tvåa, hur ska tvåan vara vriden, etc.). Under antagandet att alla bokstäver är unika får vi
uppställningar av tre kuber, eftersom kuberna kan ordnas på 6! = 3 sätt och roteras på 4^3 sätt. Men sedan kan varje uppställning ”visas upp” på 4 sätt (genom att ha ett av de fyra orden framme), så därför delar man med 4. Tycker du sånt här med att räkna sätt är skoj, kolla upp en lektion i kombinatorik som jag har lett.
På samma sätt kan man räkna ut att fyra kuber kan ordnas på
sätt och fem kuber på
sätt (under förutsättningen att alla bokstäverna är unika). Antalet sätt halveras ungefär för varje par av likadana bokstäver, men den storleksordningen blir det i alla fall.
Såklart är det mänsikligt omöjligt att testa alla sätt på begränsad tid, men lyckligtvis behöver man det inte, eftersom man kan utesluta massa fall, för att det ska ju bildas ord. Till exempel, om ordet börjar på ett ”T”, så kan inte andra bokstaven vara ”N” och den insikten sparar en 3!*4^3 = 384 fall. Så det var ju mänskligt att lösa det sista pusslet, även om det tog lång tid. Tricket är ändå att se ett ord som är med och anpassa kubuppställningen efter det. För mig var det att se början ”AO” som fick mig att tänka på ”AORTA”, som då senare gav två möjliga uppställningar av kuben, vara den ena var rätt (gav ord även på de andra sidorna: ”LIVET”, ”KENYA” och ”TITAN”).
HMT-final 2015
Finalresultat
För en dryg vecka sedan hölls finalen i Högstadiets Matematiktävling i Stockholm! 49 skarpa hjärnor var med och löste 6 matematiska problem på tid och en kom ut som vinnare. Grattis Björn Magnusson från Lund som fick fullpoäng på alla uppgifter!
På delad andraplats kom två Lundabor också, nämligen Anna-Lisa Rathsman och Hugo Eberhard. Hela resultatlistan kan du se på HMT:s hemsida.

Finalproblemen
Prova att lösa uppgifterna själv!
1. Lotta väljer slumpmässigt två olika tal bland talen 1, 2, 3, 4, 5, 6, 7, 8 och 9. Hon beräknar därefter deras produkt. Hur stor är sannolikheten att produkten är ett ensiffrigt tal?
2. Parken Parc des Mathématiques är formad som ett kvadratiskt rutnät med 5×5 trädgårdar. Två trädgårdar anses vara grannar om de har en gemensam sida (men inte om de bara har ett gemensamt hörn). Om man placerar en vakt i en trädgård så kan den vakta den parterren samt alla grannar.
a) Placera ut sju vakter i parken så att alla 25 trädgårdarna är vaktade.
b) Visa att det inte går att vakta hela parken med fem vakter.
3. I kvadraten ABCD dras fyra linjer: från hörnet A dras en linje till mitten av sidan CD, från B till mitten av sidan AD, från C till mitten av sidan AB och från D till mitten av sidan BC. Hur stor är fyrhörningen som bildas i mitten i förhållande till hela kvadraten?
4. I 3×3-rutnätet är vissa radprodukter och kolumnprodukter utsatta. Finn alla möjliga sätt att placera samtliga siffror från 0 till 8 i rutnätet så att produkterna blir korrekta.
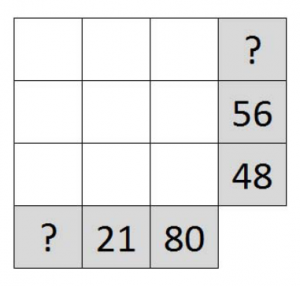
5. En oändlig talföljd a1, a2, a3,… har egenskapen att för alla positiva heltal m och n gäller
Vidare vet vi att a3 = 2015. Bestäm a2015.
6. Aladdin önskar sig tre böcker med sagor. Varje bok skall ha två tusen och fjorton sagor. Var och en av sagorna kan vara antingen spännande eller romantisk. Dock kommer hans käresta att ta en av böckerna eftersom hon också vill läsa sagor.
Aladdin förklarar för anden att han kommer läsa två sagor varje natt, en från varje bok som han har kvar. Självklart läser han dem i den ordning de står i böckerna. ”Men”, förklarar Aladdin, ”jag vill ha omväxling, så ibland vill jag ha två olika typer av sagor och ibland två lika typer, och jag kräver att vid precis hälften av nätterna få en romantisk och en spännande saga”.
Kan anden ge Aladdin tre böcker så att alla Aladdins önskemål är uppfyllda, oavsett vilken bok hans käresta tar bort?
Statistik
Tävlingen innehöll flera svåra problem. Som mest kan man få 7 poäng på ett problem, men man kan också få delpoäng. Snittresultaten blev sådana:
* Problem 1: 5.18
* Problem 2: 5.98
* Problem 3: 2.76
* Problem 4: 3.70
* Problem 5: 2.64
* Problem 6: 1.08
Så det var problem 2 som var lättast och inte problem 1 som vi i juryn trodde.
På graden kan du också se hur många finalister (y-axeln) som fick ett visst antal poäng på respektive problem.
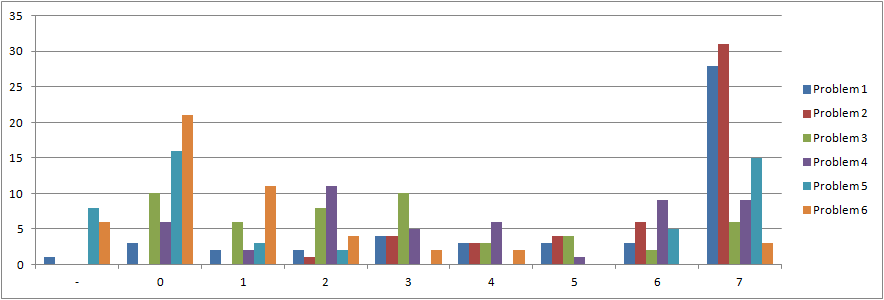
Arbetet i jurygruppen
I år var jag en av medlemmarna i jurygruppen och hjälpte till att ta fram problemen. Jag tror att juryn kan vara stolta över resultatet, då vi fick en tävling med roliga varierande problem. De flesta av dem innehöll någon twist och det var inte självklart hur man skulle lösa dem. Ändå är de möjliga att lösa eller vad tycker du? Är det något speciellt problem som du tycker är extra snyggt?
Själv gillar jag problem nummer 6 väldigt mycket. Från början hade den en annan formulering:
”Aladdin önskar sig ett rutnät med 2014 rader och 3 kolumner, där varje ruta är färgad antingen turkos eller gredelin. Han önskar sig specifikt ett rutnät som är sådant att vilka två kolumner han än väljer så är antalet rader där rutorna i de två kolumnerna har samma färg lika stort som antalet rader där rutorna har olika färg. Går det att uppfylla Aladdins alla önskningar?”
Vi valde att formulera om det till en mer konkret situation med sagoböcker. Olika människor föredrar olika formuleringar, men i slutändan ska det ju inte spela någon roll. Välj vilken formulering du vill och försök lösa Aladdin-problemet!
© 2009-2025 Mattebloggen