Lösningen till problemet för de yngre vecka 44
Mattegåta
Fem fotbollslag spelade en turnering, där alla lag mötte alla en gång. För en vinst tilldelades 3 poäng, för oavgjort 1 poäng och för förlust gavs inga poäng.
Fyra av lagen fick 1, 2, 5 och 7 poäng respektive. Hur många poäng fick det femte laget?
Diskussion
I alla för mig blir det lättare att lösa turneringsproblem, om man ritar en graf eller en tabell över resultaten.
Till exempel vet vi att ett av lagen fick 1 poäng, då kan man utan inskränkning anta att det är Lag 1. Då ser deras rad i tabellen ut som nedan.
Kolonnen är på sätt och vis motsatsen, alla förluster byts mot vinster (Lag 3, 4 och 5 vann ju mot Lag 1). Problemet går ut på att ta reda på sista radens poängsumma!
Lösning (av Nicklas Yttergren, kompletterad)
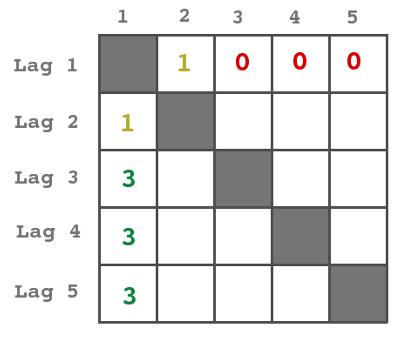
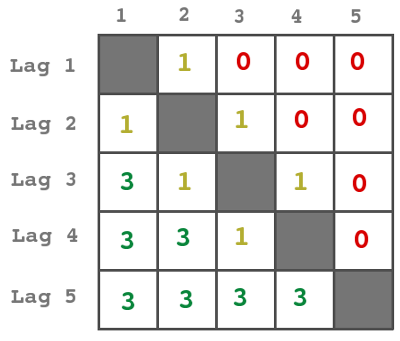
Observera hur många matcher har förlorats och hur många vunnits, de måste ha varit lika många. Totalt var det 7 förluster och 3 vinster utan att man räknat med med det femte laget (det ser man på poängen 1=1+0+0+0, 2=1+1+0+0, 5=3+1+1+0, 7=3+3+1+0).
Då måste det femte laget vunnit alla sina matcher, eftersom de spelade fyra och det är precis så många vinster som saknas. Därför fick de 12 poäng.
Matteproblem för de äldre vecka 46
Mattegåta
Visa att varje andragradspolynom kan skrivas som en summa av två andragradspolynom, vars diskriminanter är lika med 0.
Diskriminant
En diskriminant för ett andragradspolym Ax2+Bx+C är lika med
B2 – 4AC
Diskriminanter används för att bestämma ifall det finns lösningar för en given andragradsekvation och sedan beräkna dessa lösningar. Diskriminanten större än 0 ger två unika reella lösningar, lika med 0 ger en unik lösning, medan om diskriminanten är mindre än 0 så har ekvationen inga reella lösningar.
Lösningen till problemet för de äldre vecka 44
Mattegåta
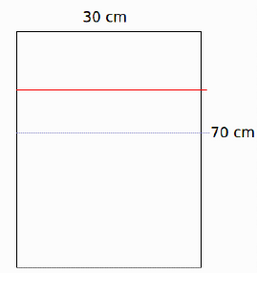
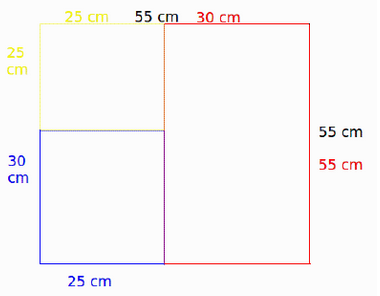
Martin samlar på ovanliga mynt. Mynten i hans samling alla har en diameter på högst 10 cm. Samlingen förvarar han i en låda som har storlek 30 cm x 70 cm (i ett lager, inga mynt ligger ens delvis ovanpå varandra).
Men nyss fick Martin ett nytt mynt med en diameter så stor som 25 cm. Visa att den nya samlingen får plats i en låda som är 55 cm x 55 cm stor (också nu i ett lager).
Diskussion
Uppgiften handlar lite om att optimera. Om vi har eventuell platsbrist i den nya lådan, så är det nog lite dumt att lägga det stora 25 cm x 25 cm-myntet i mitten utav den. Mycket smartare är det att lägga det i ett hörn.
Mynt kan även ligga på krångliga sätt, de är ju cirklar av olika storlekar. I varje mellanrum går det att stoppa in ett pyttelitet mynt till. Därför är det omöjligt att uppskatta antalet mynt och även hopplöst att försöka omplacera mynten för mycket.
Så gissningsvis ska mynten ligga ungefär som de gjorde i första lådan. Och det stora myntet ska ligga i ett hörn. Dessa två antaganden leder fram till lösningen nedan.
Lösning (av Benjamin Fayyazuddin-Ljungberg)
Rita ett rött streck 15 cm in på Martins ursprungliga låda, så att den delas in i två delar av storlek 30cm*55cm och 30cm*15 cm. Rita ett parallellt blått streck, 10 cm längre in än det röda, så att vi får två delar av storlek 30cm*45cm och 30cm*25cm.
Dela in lådan två (överlappande) rutor, ett som begränsas uppifrån av överkanten på lådan och nedifrån av det blåa strecket (storlek 30cm*25cm), och ett som begränsas uppifrån av det röda strecket och nedifrån av nederkanten på lådan (storlek 30cm*55cm).
Eftersom mynten högst har diameter 10 cm kan det inte finnas något mynt sådant att det röda strecket och det blåa strecket båda passerar genom det. Därför kan vi säga att varje mynt tillhör den rutan som helt innefattar det myntet. Alla mynt tillhör då någon ruta, och får plats i den. Det kan finnas mynt som hamnar i båda rutorna, då kan man godtyckligt välja vilken ruta de ska tillhöra.
Nu flyttar vi runt rutorna, med alla tillhörande mynt, och placerar dem i Martins nya låda. Vi ser då att vi får plats med en gul ruta i hörnet med storlek 25cm*25 cm. Alltså får det nya myntet plats också.
Lösningar till Sonja Kovalevsky-dagarnas problem 2010
Äntligen är de här, lösningarna till problemen som eleverna tävlade i under Sonja Kovalevsky-dagarna 2010!
Sonja Kovalevsky-dagarna i Stockholm 2010
För tredje gången i rad var jag med och ordnade problemlösning (tillsammans med Dag Jonsson, Magnus Carlson och min pappa) på Sonja Kovalevsky-dagarna. Tredje gånget gillt verkar det som.
Dessa dagar har som syfte att visa varför det är bra att läsa matematik och vad matematik kan användas till. Massa gymnasieungdomar från hela Sveriges samlas på något universitet (Stockholms i år) och får gå på föreläsningar och workshops.
En tradition (kanske 8 år tillbaka, nåt sånt) är att ha en liten tävling under de här två dagarna. På fredagen får eleverna en lista med problem och både under fredagen och lördagen får de lösa dem i små lag och lämna in dem.
De lag som utmärkt sig mest får priser, i år fick de en problemlösningsbok. Det visade sig att en av pristagarna redan hade boken .. med sig .. kanske därför vann han.
Annorlunda för i år jämfört med de tidigare två åren var att vi hade 1,5 timmars sessioner med varje grupp (som bestod av 4-6 lag) då de fick redovisa uppgifterna muntligt. Problemlösningsdelen på Sonja Kovalevsky-dagarna brukar ändå vara uppskattad (för att den står ut lite från det övriga programmet), men de mutliga redovisningarna tror jag gjorde det ännu bättre.
Även om det hela var lite kaotiskt ordnat, vilket hör dagarna till, så fick vi massor med bra direktrespons. Eleverna tyckte att uppgifterna var roliga och annorlunda, de fick tänka på nytt sätt. Samtidigt fick de träna i mutlig redovisning av slutledningar och tankar, något som inte alltid förekommer på vanliga mattelektioner.
Det var helt enkelt något nytt och svårt, men överkomligt för många av dem, de var trots allt de mest matematikintresserade eleverna i Sverige.
Testa själv att lösa problemen från Sonja Kovalevsky-dagarna 2010.
Ni känner kanske igen det första problemet, det har varit med på bloggen förut.
Antingen tävlar du på medelsvår nivå, då ska du lösa minst ett kvalproblem och så många medelsvåra problem som möjligt. Eller så tävlar du på svår nivå och då ska du lösa minste ett problem från varje föregående del. Observera att de svåra problemen verkligen är svåra!
Lösningarna kommer att läggas upp så fort de redigerats klart. Än så länge kan jag kontrollera era lösningar om ni skickar de till mig.
Matteproblem för de yngre vecka 45
Mattegåta
En chokladtårta är rektangelformad och sju personer ska dela på den. På tårtan finns 7 marsipanrosor:
Hur kan man dela tårtan i sju delar så att det finns en ros i varje del, om man bara får skära tårtan tre gånger och skärningarna måste vara raka linjer? Observera att delarna inte behöver vara lika stora.
Lösningen till problemet för de yngre vecka 43
Mattegåta
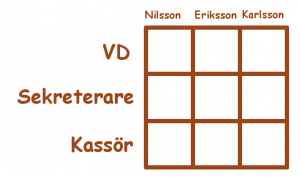
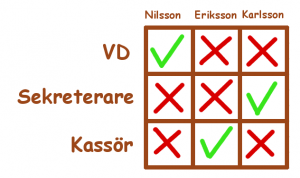
Tre vänner har ett företag ihop. Deras efternamn är Eriksson, Karlsson och Nilsson. En av dem är VD, en är sekreterare och en är kassör. Sekreteraren har inga syskon och han är den yngste på företaget. Nilsson är äldre än kassören och är gift med Erikssons syster.
Bestäm VD:ns, sekreterarens och kassörens respektive efternamn.
Diskussion
Problemet är ett typiskt exempel på en mysteriegåta. Det kanske inte är särskilt stor mystik över vem som verkligen är VD på företaget, men det är i vilket fall okänt för oss.
Om du inte vet var du ska börja, rita en tabell över alla möjligheter:
Målet att vi ska välja exakt en ruta i varje rad och varje kolonn. Då kommer precis en person bli kassör, en sekreterare och en VD.
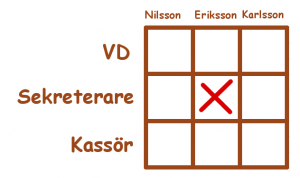
Men först måste några rutor uteslutas.Till exempel sekreterare-Eriksson-rutan (tänk på varför).
Fortsätter du på detta vis får du fram vilka rutor som är fel och vilka som är rätt. Lösningen med svaret finns längst ner.
Gillar du sådana här problem rekommenderar jag ett beroendeframkallande spel Sherlock – The Game of Logic. På sidan kan ni ladda ner ett demo och prova att spela.
Spelet går ut på sammaställa en unik person med en unik frukt, ett hus, en siffra och lite andra grejer. Till sin hjälp har man massa olika ledtrådar på den högra sidan av skärmen. De kan säga vilka saker som finns bredvid varandra (till exempel kolumnen med R måste vara bredvid kolumnen med det röda huset), ifall något är till vänster om något annat, ifall tre saker inte ligger efter varandra (åt något håll). Det finns alltid en unik lösning på slutet!

Lösning (av Toomas Liiv)
Sekreteraren har inga syskon och är yngst. Nilsson är äldre än kassören och kan därför inte vara yngst. Nilsson är gift med Erikssons syster. Eriksson har alltså minst ett syskon. Sekreterarens kriterier passar inte in på vare sig Eriksson eller Nilsson och måste därför vara Karlsson.
Nilsson är äldre än kassören och kan därför inte vara kassör, förutsatt att han inte är äldre än sig själv. Den enda kvarvarande möjligheten är VD, vilket han då också måste vara.
Kvar finns Eriksson och kassören som då måste vara samma person.
Alltså har vi att:
• VD:ns namn är Nilsson
• Sekreterarens namn är Karlsson
• Kassörens Eriksson
Matteproblem för de äldre vecka 45
Mattegåta
Ett biljardbord har en långsida som är dubbelt så lång som kortsidan. I varje hörn finns det ett hål, samt två hål till finns på varje långsidas mitt.
Vilket är det minsta antalet bollar som man kan placerat ut på bordet så att varje hål befinner sig på samma linje som ett visst par av bollar? (Bordet är rektangulärt, hål och bollar antas vara lika stora som punkter.)
Lösningen till problemet för de äldre vecka 43
Mattegåta
Nina har tre tal: 2, √2 och 1/√2.
Hon får utföra endast en operation: nämligen välja två av talen, låt oss kalla dem a och b, och ersätta dem med talen (a+b)/√2 och (a-b)/√2.
Kan Nina med hjälp av endast dessa operationer få talen 1, √2 och 1+√2 (i någon ordning)?
Diskussion
En god start är att testa och så småningom inse att man inte lyckas att få de där talen 1, √2 och 1+√2 allihop på samma gång.
För en eventuell motsägelsebevis för ett problem som handlar om någon sorts operation vore det väldigt praktiskt att hitta en invariant.
Invariant
En invariant är någonting som inte förändras under en viss given operation.
Exempel: den givna operationen är en löpares schackdrag, färgen på rutan löparen står på är då en invariant. Var rutan svart från början kommer löparen att alltid stå på en svart ruta (för den går bara diagonalt) Om rutan var vit från början kommer den alltid att stå på vitt.
Ifall vi hittar någonting som inte ska förändras även när Nina bytt ut två tal enligt regeln, så ser vi att det som frågas efter inte går att genomföra om egenskapen skiljer sig mellan start- och slutposition.
Det svåra består i att hitta rätt invariant!
Lösning (av Johan Björklund)
Antag att de tre talen är a, b, c.
Efter en operation så är de tre talen (a-b)/√2, (a+b)/√2, c.
Undersök summan av kvadraterna på talen. Innan så är den a2+b2+c2.
Efteråt så är den 0.5(a-b)2+0.5(a+b)2+c2=a2+b2+c2. Summan ändras alltså inte under operationen.
I vårt fall så har vi 22+√22+(1/√2)2 ≠ 12+ √22+(1+√2)2 (uppenbart då √2 inte är rationellt). Motsägelse.