Mattegåta
Hitta två äkta bråk, det ena med nämnaren 8 och det andra med nämnaren 13, så att differensen mellan det största och det minsta av dem är så liten som möjligt.
Diskussion
Vad menas med att ett bråk är äkta? Det är ett bråk vars täljare är mindre än dess nämnare (och båda är positiva heltal). Exempel på äkta bråk är  och
och  . Ett äkta bråk har alltså alltid ett värde mellan 0 och 1!
. Ett äkta bråk har alltså alltid ett värde mellan 0 och 1!
Nu har vi ett lite fuskigt sätt att lösa problemet, de äkta bråken med nämnare 8 respekrtive 13 är ju inte så många! För att gissa svaret kan man sätta ut alla äkta bråks värden på tallinjen. Tag nämligen sträckan mellan 0 och 1 och dela in i åtta lika stora delar. På markeringarna har vi bråken  och
och 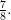

Samma sak kan göras med trettondedelar, men det är lite för plottrigt att göra det på samma bild, eller hur? Det vore smidigare att rita en exakt bild, där  och så vidare är utsatta, om sträckan hade en naturlig uppdelning i just 13 delar. Med andra ord, om antalet markeringar kan delas både med 8 och med 13, så är det ganska lätt att se skillnaden mellan bråken också.
och så vidare är utsatta, om sträckan hade en naturlig uppdelning i just 13 delar. Med andra ord, om antalet markeringar kan delas både med 8 och med 13, så är det ganska lätt att se skillnaden mellan bråken också.
Därför söker vi talens minsta gemensamma multipel, med andra ord det minsta positiva heltalet som både är delbart med 8 och med 13. Minsta gemensamma multipel betecknas också MGM. Och den största gemensamma delaren betecknas SGD, det behövs för att bestämma MGM av 8 och 13.
Lösning (av Toomas Liiv)
SGD(8,13)=1. Nämnarna är relativt prima.
MGM(8,13)=8*13=104, vilket också är minsta gemensamma nämnare till bråken.
Differensen av det största och minsta bråket kommer också att kunna skrivas med nämnaren 104 som ett äkta bråk. Det minsta sådana bråket är  , vilket uppnås med bråken
, vilket uppnås med bråken  och
och  , men dessa är olyckligtvis inte äkta bråk.
, men dessa är olyckligtvis inte äkta bråk.
Det näst minsta bråket med nämnaren 104 är  , vilket ger oss ekvationerna
, vilket ger oss ekvationerna

och

som efter division med 104 kan skrivas som

och
 .
.
Den första ekvationens minsta positiva lösning är 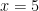 och
och  . Den andra ekvationens minsta positiva lösning är
. Den andra ekvationens minsta positiva lösning är 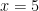 och
och  .
.
Detta ger oss att

och att

Lösningen till problemet är alltså 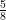 och
och  eller
eller  och
och  .
.