kval – Mattebloggen

Lösningar till SMT-kvalet 2014

Detta är de inofficiella (dagen-efter) lösningar till SMT-kvalet som hölls den 30:e september på gymnasieskolorna över hela Sverige. De officiella lösningarna kommer att komma upp på SMT:s hemsida.

Problem 1

Ett tåg kör fram och tillbaka dygnet runt mellan Aby och Bro med lika långa uppehåll vid ändstationerna, och med samma tidtabell alla dagar i veckan. Under varje resa stannar tåget endast en gång, vid Mo.

Jens åker med tåget från Aby, stiger av i Mo för att handla och återvänder till Aby när tåget nästa gång stannar i Mo. Hans uppehåll i Mo har då varat i 50 min. Jenny åker från Bro till Mo, och åker sedan hem nästa gång tåget stannar på väg mot Bro. Hennes uppehåll i Mo blir 30 min.

Hur många gånger stannar tåget i Mo under ett dygn? Vi bortser från den tid det tar för tåget att stanna till i Mo, samt antar att tåget är i rörelse vid midnatt.

Lösning

Puh, den första uppgiften testar om du kan läsa mycket text! :)

Vi noterar att under tiden Jens är i Mo, så hinner tåget åka från Mo till Bro, stå i Bro och sedan åka tillbaka från Bro till Mo precis. Under tiden som Jenny är i Mo, så hinner tåget att göra precis rester, det vill säga åka från Mo till Aby, stanna i Aby och sedan åka tillbaka från Aby till Mo. Eftersom vi antar att tåget inte spenderar tid i Mo, så utgörs hela cykeln av de två tiderna. Det vill säga, det tar 80 minuter för tåget att göra sin rutt.

Under dygnets 24*60 minuter hinner tåget göra rutten 24*60/80 = 18 gånger. Under varje rutt stannar tåget i Mo två gånger. Således blir det 36 stopp i Mo under ett dygn.

Problem 2

Medelvärdet av 12 reella tal är 20. Medelvärdet av de tal som är större än 20 är 27, medan medelvärdet av de tal som är mindre än 20 är 17. Visa att minst ett av de talen måste vara lika med 20.

Lösning

Vi antar motsatsen: Det finns inget tal bland de 12 som är lika med 20. Då utgörs talen av k stycken som är större än 20 och 12-k stycken som är mindre än 20.

Talens medelvärde är 20, alltså är alla talens summa lika med 20*12 = 240. De som är större än 20 har på samma sätt summan k*27 och de som är mindre har summan (12-k)*17. Således har vi:

20*12 = 27*k + 17*(12-k) = 17*12 + 10*k

3*12 = 10*k

3,6 = k

Motsägelse, eftersom k var ett antal. Alltså måste det finnas som minst ett tal som är exakt 20.

Problem 3

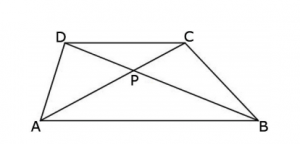
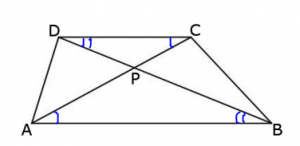
Pukterna P, Q, R, S väljs på sidorna av kvadraten ABCD, så att P ligger på AB, P på BC, R på CD och S på DA, och så att sträckorna AP, BQ, CR, DS är lika långa. Punkten M inuti kvadraten ABCD är sådan att arean av fyrhörningen SDRM är 24 cm², arean av RCQM är 41 cm² och arean av QBPM är 70 cm². Bestäm arean av fyrhörningen PASM. (Du kan ta för givet att det finns en punkt M som uppfyller villkoret.)

Lösning

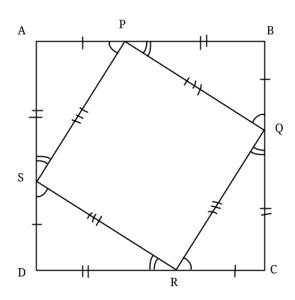
Om AP = BQ = CR = DS, så är PB = QC = RD = SA, då kvadratens sida är lika med AP + PB = BQ + QC = CR + RD = DS + SA. Därför får vi, om vi drar linjerna PQ, QR, RS, SP, fyra kongruenta rätvinkliga trianglar på bilden (kongruensfall SVS till exempel).

Det betyder att PQ = QR = RS = SP, samt att alla vinklar i PQRS är räta, då de komplementerar två vinklar, vars summa är 90^°. PQRS är således en kvadrat.

SMT_k14_3_1

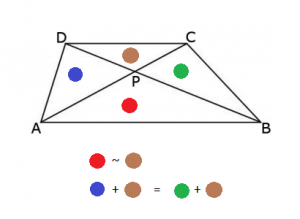
Låt oss betrakta fallet då punkten M hamnar inuti kvadraten PQRS. Dra då de fyra höjderna från M mot den lilla kvadratens sidor. Höjdernas respektive längder betecknar vi med a, b, c, d. Notera att a + c = b + d, då dessa höjder bildar sträckor, parallella med kvadratens sidor. Alltså har summorna samma värde som längden av den inre kvadratens sida.

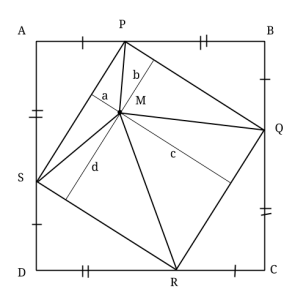
SMT_k14_3_10

Låt oss beteckna den inre kvadratens sida med x. Det betyder att vi kan uttrycka areorna av trianglarna MSP, MPQ, MQR, MRS:

$\displaystyle S_{MSP} = \frac{a\cdot x}{2}$
$\displaystyle S_{MPQ} = \frac{b\cdot x}{2}$
$\displaystyle S_{MQR} = \frac{c\cdot x}{2}$
$\displaystyle S_{MRS} = \frac{d\cdot x}{2}$

Då a + c = b + d får vi att:

$\displaystyle S_{MSP} + S_{MQR} = S_{MPQ} + S_{MRS}$

Då måste även

$\displaystyle S_{PASM} + S_{RCQM} = S_{QBPM} + S_{SDRM}$

då vi lägger på areor av två av de kongruenta trianglarna på båda sidor (gula på bilden).

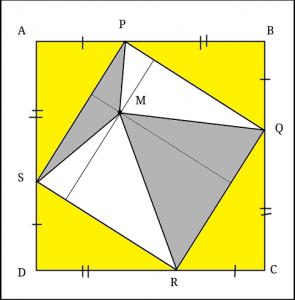
SMT_k14_3_2

Alltså är arean av fyrhörningen PASM lika med 24 + 70 – 41 = 53cm².

Men vad händer om punkten M ligger utanför den inre kvadraten? Egentligen fungerar exakt samma lösning, men man måste tillåta att vissa areor är negativa. Till exempel om M ligger inuti triangeln APS ligger, så betraktar vi längden av höjden a som ett negativt värde, liksom arean av triangeln MPS. Alla andra påståenden i vår lösningen gäller även med den modifikationen, alltså blir svaret i vilket fall densamma. Det vill säga 53cm².

Problem 4

Sträckorna AP och BQ är höjder i triangeln ABC. Triangelns vinkel vid hörnet C är 100^°. Punkten M är mittpunkt på sidan AB. Bestäm vinkeln PMQ.

Lösning

Eftersom triangeln är trubbvinklig går höjderna AP och BQ utanför triangeln och skär förlängningen av BC respektive AC.

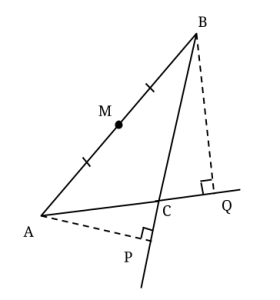
SMT_k14_4_1

Om man ritar ut cirkeln med mittpunkten M och diametern AB, så kommer punkterna P och Q hamna på cirkelns rand, eftersom de står på diameter med räta vinklar. (Se randvinkelsatsen.) C hamnar inuti cirkeln, eftersom ACB > 90^°

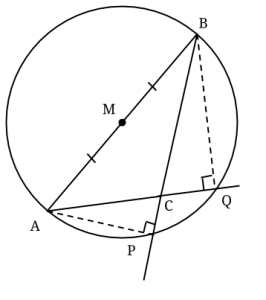
SMT_k14_4_2

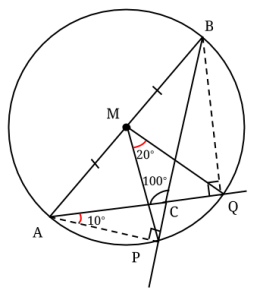
Eftersom vinkeln ACB är 100^°, så är komplementvinkeln ACP lika med 80^°. Det betyder att vinkeln CAP är lika med 10^°, då vinkeln APC är rät. På samma sätt är CBQ = 10^°, fast det kommer vi inte att använda.

SMT_k14_4_3

Dags att använda radvinkelsatsen igen! Då vinklarna PAQ och PMQ står på samma båge, men den första är en randvinkel medan den andra är en centralvinkel, så följer det att PMQ är dubbelt så stor, det vill säga lika med 20^°.

SMT_k14_4_4

Problem 5

I en skolklass får en elev en påse med 2014 enkronor från läraren medan de övriga eleverna inte har några pengar alls. Varje gång två elever träffas delar de pengarna de har tillsammans lika om det är ett jämnt antal kronor, medan de lägger en krona i klasskassan och delar lika på resten om de har ett udda antal kronor tillsammans. Efter lång tid har detta hänt många gånger och det visar sig att alla pengarna ligger i klasskassan. Hur många elever måste det minst ha varit i klassen?

Lösning

Det gäller att komma på ett svar, visa att händelsen var möjlig vid det svaret, samt förklara varför ett mindre antal elever aldrig skulle fungera.

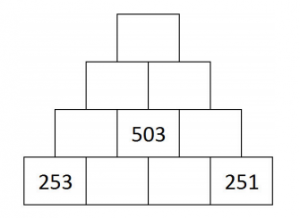
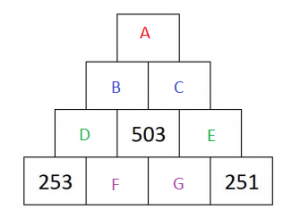
Mitt svar är 12 elever. Låt oss ställa dem på rad, med eleven med 2014 kronor först. Därefter delar första och andra eleven på pengarna, andra och tredje, tredje och fjärde och så vidare upp till att tionde och elfte delar på pengarna. Vi får efter det följande mängder hos eleverna (och några kronor ligger i klasskassan):

1: 1007 kr
2: 503 kr
3: 251 kr
4: 125 kr
5: 62 kr
6: 31 kr
7: 15 kr
8: 7 kr
9: 3 kr
10: 1 kr (precis innan hade hen 3 kr)
11: 1 kr (precis innan hade hen 0 kr)
12: 0 kr

I denna situation kan elev 10 och elev 11 bli av med pengar genom att dela dem med elev 12, en i taget.
På så vis ”försvann” 3 kr från en elev med hjälp av två andra elever som hade 0 kr. Därför är det möjligt, att i flera steg få bort 3 kr från elev 9 (eftersom det finns minst två elever med 0 kr). Notera att elev 9 hade 7 kr innan hen delade med sig för första gången vidare i raden. Därför har vi ett sätt att bli av med 7 kr med hjälp av tre ”tomma” elever. Därför kan vi bli av med elev 8:as 7 kr också.

Vi fortsätter på samma sätt tills elev 1 är den enda som har pengar (1007 kr) kvar. Hen kan bli av med dem (mha av de andra tomma eleverna), eftersom elev 2 kunde göra det. Alltså kan man bli av med alla pengar i det här fallet.

Varför räcker det inte med 11 elever?

Notera att i en situation då vi har en mängd elever som kan göra operationerna med varandra, och då alla har åtminstone m mynt, kommer ingen nånsin att kunna få färre än m mynt. För det skulle krävas att man delade som mest på 2(m – 1) + 1 = 2m – 1 mynt, men det är mindre än vad två godtyckliga personer i mängden har tillsammans.

Om klassen hade haft två personer skulle de bara kunna ha 1007 mynt var och inte kunna minska på den mängden. Vi ska visa att om tre personer får byta så kommer var och en att ha som minst 503 kr, om fyra personer får byta så kommer de ha som minst 251 kr var och så vidare. Om 11 personer får byta kommer de alltid ha som minst 1 kr var. Då kommer vi att ha visat att inte alla pengar kan hamna i kassan.

I fallet med tre personer, titta på när den sista personen blir involverad för första gången. Hen delar då pengar med en person som har minst 1007 kr (enligt vad vid visade om två personer). Den själv har 0 kr, alltså kommer de efter delningen att få minst 503 kr var. Nu har alla tre personerna minst 503 kr (den som inte var med om den sista delningen har minst 1007) och kan inte få färre.

På samma sätt går vi steg för steg (eller med induktion) och betraktar då k+1 personer får vara involverade. När den sista av dem gör sin första delning så blir dess minimum hälften av minimum för k personer, avrundat neråt. Ingen annan har mindre än det minimivärdet. Således har vi visat att minsta antal kronor hos varje person bland 11 är 1 kr (och med färre personer ännu större), det vill säga de fallen fungerar inte för att bli av med hela kassan.

Problem 6

Låt a och b vara två positiva heltal sådana att 8a² + 2a = 3b² – b . Visa att både 2a + b och 4a – 2b + 1 är kvadrater av heltal.

Lösning

Min lösning var inte världens snyggaste från början, men här en så kallad ”kammad” lösning. Det vill säga onödiga steg har tagits bort. Låt dig inte luras av att lösningen är kort, det tog några försök att komma fram till den.

Låt oss multiplicera de talen vi ska visa vara kvadrattal:
(2a + b)(4a – 2b + 1) = 8a² – 2b² + 2a + b = (8a² + 2a) + (- 2b² + b)

Den första termen kan vi ersätta med 3b² – b så som det är givet av villkoret i uppgiften:
(2a + b)(4a – 2b + 1) = (3b² – b) + (- 2b² + b) = b²

Så vi vet att produkten av talen är ett kvadrattal i alla fall.

Notera att ett kvadrattal har alltid ett jämnt antal av samma primfaktorer i sin primtalsfaktorisering, så det lönar sig att titta på något primtal p, ta något sådant som ingår i faktoriseringen av både 2a + b och 4a – 2b + 1. Det implicerar att b² är delbart med p ocskå. Eftersom p är ett primtal, så måste även b vara delbart med p.

Om både 2a + b och b är delbara med p, så är 2a det också. Låt oss nu titta på 4a – 2b + 1 igen: 4a är delbart med p, b är delbart med p, alltså ger talet rest 1 vid division med p. Detta ger motsägelse, alltså kan inte 2a + b och 4a – 2b + 1 har gemensamma primfaktorer. De är alltså relativt prima.

Det innebär att varje primfaktor som b² har i faktoriseringen (ett jämnt antal gånger) antingen ingår helt i ena talet eller det andra. Det innebär att vart och ett av talen har alla primfaktorer i jämna potenser och alltså är kvadrater av heltal.

HMT-kval 2013

För circa en månad sedan hölls kvalomgången i Högstadiets Matematiktävling. Det är en tävling i problemlösning som riktar sig till årskurs 6-9, men självfallet lyckas eleverna i årskurs 8-9 få bäst resultat. Därför är det mest elever från dessa årskurser som går vidare till finalomgången.

Därmed inte sagt att de inte kan gå bra för elever i åk 6-7! Det de eventuellt saknar är några kunskaper om geometri samt delbarhet, vilket ett par av årets kvaluppgifter gick ut på. Däremot kunde man klara sig riktigt bra även om man ”bara” hade löst fyra uppgifter av sex. 10 poäng räckte nämligen för att gå till final (3 poäng tilldelas för varje korrekt löst uppgift). Du kan läsa mer om årets omgång på HMT:s hemsida, medan vi tittar närmare på själva uppgifterna.

Problem 1

Det går att skriva tal i rutorna i ﬁgur 1 så att om man följer pilen från en ruta och
använder räkneoperationen som står vid pilen så får man talet i nästa ruta.

Vilket tal är då X? Ange även en möjlig räkneoperation att ersätta frågetecknet med.

Lösning

Strategin är att gå baklänges från 13 till X på vägen gjord av pilarna till vänster. Till 13 kommer vi genom att dela med 2, så talet innan måste vara 26. Till 26 kommer vi genom att subtrahera 1, så talet innan är 27. Innan dess multiplicerade vi talet med 3, så talet innan måste ha varit 9. Och från X kom vi till 9 genom att subtrahera 11, så X måste ha varit 20.

På samma sätt kan vi bestämma talen på högra pilvägen. Till 13 måste vi ha kommit från 18, till 18 från 12, till 12 från 6. Om vi ska komma från 20 till 6 så kan operationen under frågetecknet vara -14 till exempel.

Kommetarer

Det här en typiskt uppgift nästan alla tävlande klarar av. Man hoppas ju innerligt att ALLA elever i åk 9 ska kunna klara av en sådan uppgift. Men så är tyvärr inte fallet, vilket bara beror på att dessa elever antagligen skulle missförstå uppgiften.

En grej man inte tänker på när man är van vid ekvationer är att ”x2” och ”x3” skulle kunna misstolkas att handla om ”X”. Bokstaven ”X” står i mitten för att göra uppgiftsformuleringen tydligare, men kan tvärtom skrämma elever som inte gillar ekvationer. Man skulle kunna ställa upp lösningen på första halvan av uppgiften såhär:

((X – 11)*3 – 1)/2 = 13

Men hur kul formulering är det? Vilken av formuleringarna uppmanar till någorlunda kreativt tänkande och vilken till att ”komma ihåg och tillämpa inlärd metod”? Just det, olika formuleringar på samma uppgift blir pedagogiskt sett helt olika uppgifter! De flesta elever tror jag skulle lyckas lättare på den första formuleringen. Något att tänka på när man introducerar ekvationer i skolan.

Problem 2

Om talet A vet vi följande:
- Talet A ger resten 5 när det delas med 11.
- Talet A ger resten 4 när det delas med 9.
- Talet A ger resten 5 när det delas med 7.
- Talet A ger resten 4 när det delas med 5.
Vilken rest får man när man delar A med 3?

Lösning

Svaret kan vara antingen 0, 1 eller 2, eftersom inga andra rester förekommer när man dividerar med 3. Talet A kan vara hur stort som helst, men vi försöker ”få plats” med så många 3:or i talet som det bara går.

För det kan vi använda att talet A har rest 4 när det delas med 9. Det betyder att man får plats med ett antal 9:or och det blir 4 över. Men en 9:a är ju tre 3:or, därför vet vi att talet A innehåller ett ännu större antal 3:or, men det viktigaste är att det blir 4 över. Där får det plats en 3:a till och det blir 1 över. Därför är resten lika med 1.

Kommetarer

Svårigheterna med att lösa den här uppgiften består av att man inte vet vad division med rest innebär, eftersom man inte fokuserar så mycket på just rester i skolan. Och även om man vet vad resten är, så kanske man försöker bestämma talet A, vilket inte ger ett heltäckande resultat (det finns flera tal A som har de nämnda egenskaper, till och med oändligt många sådana tal finns det). Och så är det förstås vilseledande att det bara villkor två som är viktigt.

Tar man sig igenom de hindren, så är inte uppgiften svår.

Problem 3

På Skänkvägen står elva hus på rad, numrerade från 1 till 11. Eftersom sämjan bland
grannarna är god, så bjuds det ofta på middag. När man bjuder på middag bjuder man
in de två närmaste grannhusen på båda sidor. Om man inte har två grannar på någon
sida bjuder man alltså in färre grannar, till exempel bjuder hus 2 in grannarna i hus 1, 3
och 4.

En dag ärver familjen i hus 2 en riktigt, riktigt ful tavla. När familjen nästa gång blir
bjuden på middag bestämmer man sig därför att ge bort tavlan till kvällens värd. Men
tavlan är så ful att ingen på gatan vill behålla den, så vid första möjlighet ger man därför
bort den till den middagens värd. Av artighetsskäl kan man såklart inte ge tillbaka tavlan
till någon man själv fått den av, och inte heller till någon man själv redan en gång givit
bort den till.

Vem kommer till slut att vara tvungen att behålla tavlan?

Lösning

Vi hoppar vilt i svårighetsnivån! Vi ”finkammar” uppgiften lite först, för att senare lättare kunna formulera lösningen.

Man kan bara ge bort/ta emot tavlan av hus som ligger 1 eller 2 steg bort ifrån ens eget. Om hus A gav bort tavlan till hus B så är den förbindelsen A-B ”förbrukad” eftersom tavlan inte får ges på samma sätt och inte heller ges tillbaka från hus B till hus A. Således kan vi rita ut alla förbindelser och tänka oss att tavlan vandrar längs med dem och ”förbrukar” dem (husen ligger på rad, men att vi ritar dem på en cirkel spelar ingen roll, det är förbindelseschemat som är det viktiga):

tavlan

Låt oss för en stund strunta i var tavlan börjar sin väg (hus 2). Vi tänker istället på var tavlan kan sluta (någon annanstans i hus 2?). Kanske slutar tavlan i hus 4, så vi tittar på förbindelser som har med hus 4 att göra:

tavlan_hus

Om hus 4 är huset som inte kan skicka tavlan vidare, så betyder det att tavlan kom till dem och i och med det var alla förbindelser förbrukade. Hur förbrukades förbindelserna? Varje gång hus 4 fick tavlan så förbrukades nästa förbindelse genom att de gav bort den, och tvärtom. Så eftersom tavlan inte började där, måste förbindelserna förbrukats i ordningen: fick – gav bort – fick – gav bort. Därför kunde inte hus 4 fått tavlan på sin sista förbindelse.

Husen 3, 5, 6, 7, 8, och 9 befinner sig i samma situation. De har fyra förbindelser var och därför följer samma schema, om nu alla fyra förbindelserna skulle förbrukas: fick – gav bort – fick – gav bort.

Samma sak är det egentligen för husen 1 och 11 som har två förbindelser var. Får de tavlan, så har de ju möjlighet att ge bort den.

Därmed är det bara hus 2 och 10 kvar. Hus 2 har tavlan från början och därför följer schemat ”gav bort – fick – gav bort”, OM vi är säkra på att alla förbindelser förbrukas. Därför är hus 10 det enda huset som kan ha kvar tavlan utan att kunna ge bort den.

En möjlig väg för tavlan kan vara 2 -> 4 -> 6 -> 8 -> 10 -> 11 -> 9 -> 10. Nu kan hus 10 inte ge bort tavlan.

Kommetarer

Läsaren som är bekant med grafteori förstår att så fort vi har ”kammat” problemet så handlar det om i princip Eulerstigar. Men enkel formulering kan man säga att en figur, som man ritar utan att lyfta pennan från pappret, har som mest två punkter, varifrån det utgår ett udda antal linjer. En av punkterna kommer då vara startpunkten och den andra slutpunkten.

Problem 4

I parallelltrapetset ABCD är sidan AB 50% längre än sidan CD. Punkten P
är diagonalernas skärningspunkt. Arean av triangeln ADP är 12. Bestäm arean av hela
parallelltrapetset.

Lösning

Parallelltraps är en figur med två parallella sidor (det syns på bilden att det är AB och CD som är parallella). Om man ritar ut diagonalerna bildas det flera alternatvinklar, varav två par är inbördes lika. Det följer då att trianglarna APB och CPD är likformiga.

alternatvinklar

Vi färgkodar de fyra små trianglarna som syns på bilden:

parallelltrapets_slutsatser

Vi kom fram till att brun och röd var likformiga. De är dessutom likformiga med koefficienten 1,5 (eftersom röds motsvarande sida var 50% länge än bruns).

Vi vet även att blå+brun har samma area som grön+brun, eftersom båda dessa stora trianglar har samma bas DC och lika lång höjd (avståndet mellan de parallella linjerna). Därför har blå och grön samma area och vi vet från uppgiften att det är 12.

Blå och röd har samma höjd om vi tar DP pch PB som baser. Med DP och PB är motsvarande sidor hos den bruna och den röda triangeln. PB är alltså 1,5 gång större och då han även röd 1,5 gånger större area än blå, 12*1,5 = 18.

Blå och brun delar höjd om man nu väljer AP och PC som baser. Även här är PC 1,5 gånger mindre än AP. Så arean för brun är även den 1,5 mindre än arean för blå, det vill säga 12/1,5 = 8.

Därmed har vi bestämt alla de små trianglarnas areor. Arean för hela parallelltrapetser är
röd + brun + grön + blå = 18 + 8 + 12 + 12 = 50 (areaenheter)

Kommetarer

Måste erkänna att jag försökte lösa den här uppgift snabbt och misslyckades! Hade en alldeles för avancerad lösning och räknade fel någonstans på vägen. Så här ska man kunna ”lagom” mycket geometri :)

”Lagom” mycket geometri innebär bland annat: parallellitet, alternatvinklar, vertikalvinklar, likformiga trianglar, likformighetskoefficient, arean för en triangel, val av bas/höjd i en triangel. Inte så lite man ska kunna!

Framför allt ska man vara skolad för att genomföra bevis för att redovisa uppgiften på ett korrekt sätt. Geometriundervisningen som bygger på axiom/bevisföring har i princip försvunnit från svenska skolor, därför lyckades nästan ingen av deltagarna lösa (eller ens få poäng) på den här uppgiften. Jag tvivlar på att särskilt många gymnasister skulle kunna lösa den här uppgiften heller.

Problem 5

Genom att ﬂytta om siffrorna i talet 2013 kan man få 18 olika fyrsiﬀriga tal. På hur många
sätt kan man välja två olika av dessa 18 tal så att deras summa är precis lika med ett av
de återstående 16 talen?

Lösning

Provar man lite så ser man att det här aldrig går. Hur förklarar vi det här på ett allmängiltigt sätt?

Om två tal som bara består av siffrorna 0, 1, 2 och 3 adderas, så kommer entalen, tiotalen, hundratalen samt tusentalen adderas var för sig, eftersom siffrorna är så pass små. Men det betyder att siffersumman för resultatet av additionen kommer vara lika med siffersumman för det första talen adderat med siffersumman för det andra talet.

Detta kan ju inte hända, eftersom siffersummorna för alla talen är 6. Därför kommer siffersumman för resultatet att bli 12 och det kan inget av talen i uppgiften ha.

Kommetarer

Den här uppgiften kan lösas på mängder av olika sätt, jag angav det kortaste jag kunde komma på. Sätter eleven in sig i uppgiftens formulering, så är resultatet mer eller mindre uppenbart. Hur man ska förklara resultatet är däremot inte lika uppenbart.

Jag tror att många elever känner intuitivt att det har med siffersumman att göra, men de är inte vana vid att formulera lösningar på det sätt, med bevarande av siffersumma och dylika termer. Därför gissar på att de använde mer krångliga förklaringar. Det kan vara frustrerande att försöka förklara något som är så pass uppenbart, men en bra övning om man vill bli bättre på att förstå och formulera egna bevis.

Problem 6

Rutnätet i ﬁguren skall fyllas med tal. I varje ruta (utom i understa raden) står summan
av de två talen i rutorna direkt under den. Vilket tal skall stå i den översta rutan?

Lösning

Den här uppgiften kan både lösas baklänges (nerifrån och upp) och framlänges (uppifrån och ner). Istället för att bara införa två variabler inför vi jättemånga, det vill säga betecknar varje okänt tal med en bokstav.
talpyramid_variabler

Talet A består av talen B och C.

Talen B och C består av talen D och 503 och 503 och E.

Talen D och 1006 och E består av talen 253 och F och 1006 och G och 251. Totalt alltså 1510 och F och G.

Inte har vi kommit fram till svaret än, men vet att pyramidegenskapen även gäller talet 503: att det består av talen F och G.

Så vi vet att talet A består av 1510 och F och G, med andra ord av 1510 och 503, det vill säga lika med 2013. Klart!

Kommetarer

Även här tror man kanske att hela pyramiden måste bestämmas för att avgöra det översta talet, men så är inte fallet. Det finns flera olika pyramider som ser ut på det sättet och alla måste då ha 2013 i toppen. Notera att det är på samma sätt som i uppgift 2 och uppgift 4 – flera olika konstruktioner uppfyller uppgiftsvillkoren, men ger ändå ett och samma svar i slutändan.

Ibland (eller kanske alltid) går matematik ut på att dra korrekta och allmängiltiga slutsatser i situationer där vi inte har tillgång till fullständig information.

Öva på geometri inför SMT-kval

Kvalomgången i Skolornas matematiktävling sker imorgon. Om du vill fräscha upp era geometrikunskaper inför tävlingen
här står det korfattat vad du behöver plugga på. Notera att minst ett av problemen på tävlingen är ett klassiskt geometriproblem.

Tyvärr har de flesta deltagare nackdelen att inte ha gått igenom så mycket geometri i skolan. Har man övat på geometriproblem åtminstone några gånger, har man en stor fördel där, eftersom geometriproblemen är inte särskilt svåra (de algebraiska problemen på SMT kräver oftast fler icke-triviala insikter).

Några användbara geometrisatser har jag samlat i en cirkellektion i geometri. Vi pratade om följder av randvinkelsatsen och användningen utav dessa följder i problem om figurer som kan skrivas in i cirklar.

Kan du göra rätt på övningarna samt på de första fem problemen så har du fått hum om hur geometriproblem skall bevisas. Då kan du gå över till de svårare problem, som jag har hämtat från riktiga SMT-kvalomgångar. Notera dock att lektionen inte täcker geometriska tekniker som likformighet, areor, samt sinus- och cosinussatsen. Det finns så pass mycket användbar geometri, så att det inte får plats i enda lektion.

Lycka till på tävlingen! Skriv gärna i kommentarerna hur det har gått för dig och om tipsen har hjälpt :)

Öva på delbarhet och ekvationer inför SMT-kval

Skolornas matematiktävling närmar sig med stormsteg, nu är det bara en vecka kvar! Jag har skrivit tips inför tävlingen förut, men om du träna på verkliga problem, rekommenderar jag att kolla på vår cirkellektion, som handlade just om delbarhet, ekvationer och olikheter.

Under lektionen bevisade vi alla de viktiga fakta man använder inom de områden när man löser tävlingsproblem och diskuterade kontrollfrågor. För att lyckas bra i tävlingen bör du kunna svara på i princip alla kontrollfrågor!

Försök sedan att lösa problem 1-4. De första tre problemen kommer från riktiga SMT-tävlingar, men jag skulle rekommendera att börja med problem 2 eller 4, eftersom de är lättast att lösa. Sedan ta dig an 1:an och till sist 3:an.

Tips inför SMT-final

Som vanligt lite sent kommer det några tips inför morgondagens tävling! De allmäna tävlingstipsen gäller förstås fortfarande.

Saker som är bra att kunna inför finaltävlingen utöver det man ska kunna inför kvaltävlingen:
– Triangelolikheten
– Största sida ligger mittemot största vinkeln i en triangel, minsta mittemot minsta
– Bisektrissatsen och förhållandet i vilken medianernas skärningspunkt delar medianerna
– Homoteti och inversion (om du är proffs och kan allt annat :))
– Linjens ekvation
– Vad polynom är för något, faktorisering och division med rest
– Grundläggande sannolikhetsteori
– Diofantiska ekvationer
– Grundläggande kombinatorik

Bevistekniker som är bra att kunna inför tävlingen:
– Induktion
– Insättning av specialfall i funktionalekvationer och härledning av fukntionens egenskaper (jämn, udda, linjär, kvadratisk etc.)
– Invarianter och halvinvarianter

Problemen i finalen är svåra, men det handlar framför allt att komma på finurliga lösningar och inte särskilt mycket om att kunna matematiska termer. Mitt största råd är att koncentrera sig på problemen där man har fullt koll på matematiken. Försök på alla problemen litegrann, men försök seriöst på ungefär fyra av problemen. Ibland krävs helt enkelt en timmes koncentration för att komma på en lösning!

Och sist men inte minst: lycka till!!!!!

Tips inför SMT-kval

Nu är det bara några timmar kvar till SMT-kval och jag tänkte dela av mig med mina tävlingstips.

Allmänna tävlingstips:
– Ha skoj! Det här är bara en tävling.
– Slösa inte bort tiden, fem timmar kan gå väldigt fort! Gör ett gott försök att lösa varje problem, men spendera inte mer än en halvtimme om du inte kommer nånvart.
– Läs problemtext noga. Det är bättre att ställa en fråga till läraren än att försöka lösa ett annat problem än det som står.
– Om du tror att du har löst uppgiften, läs texten noga igen. Skriv ner lösningen direkt. Eventuella fel eller obevisade påståenden brukar dyka upp först när du skriver ner resonemanget.
– Bara ett svar ger oftast 0 poäng, men en ofullständig lösning kan ge upp till 6. Skriv alltså ner alla idéer du har på problemen tydligt. Om du har en plan för lösningen, men inte kan bevisa alla stegen, skriv ner planen.

När du inte har någon aning om hur du ska lösa uppgifterna, finns det några olika tekniker du kan prova:
– Undersök ett enkelt fall av problemet. T.ex., om det handlar om en 8×8-kvadrat, prova att göra samma sak med en 4×4-kvadrat eller även 2×2.
– Kolla specialfall. Svaren kan t.ex. vara olika för jämna och udda n. Prova att sätta in några tal och se om du upptäcker samband eller mönster. Om det är en funktionalekvation, stoppa in 0 iställer för x och sedan ocskå 1, -1, 2, -2, -x.
– Är det en geometriuppgift, rita figuren så nogrannt som möjligt! Då kan du t.ex. ”se” vad svaret ska bli för något. Och om du vet svaret, t.ex. att en vinkel ska vara lika med 45 grader, blir det lättare att bevisa det.
– Kom ihåg att olika bilder kan uppstå i geometriuppgifter. Ett missat fall (t.ex. en punkt ligger inuti en cirkel och du har bara kollat när den är utaför eller på) kan ge avdrag.
– Att rita en bild underlättar även lösning av uppgifter, som inte är geometri.
– Anta saker ”utan inskräkning” så att det blir lättare att jobba med problemet. T.ex. i en olikhet som är symmetrisk med avseende på a, b och c (det vill säga att man kan byta plats på två av bokstäver och olikheten förblir densamma) kan man anta att a>=b>=c.

Lite saker bör du kunna för att lösa många av uppgifterna:
– Hur man faktoriserar tal i primtal. Delbarhetsprinciperna för 2, 3, 4, 5, 9 och 11.
– Uppställning för aritmetik för tal i bas tio (dvs talteoriproblem som handlar om siffror löses med att kolla på sista siffran först etc.)
– Olikheten mellan aritmetiska och geometriska medelvärdet och några relaterade olikheter (t.ex. a+1/a>=2 för positiva a). De flesta olikheterna går ut på att man ska få ”nånting i kvadrat >= 0”.
– Sinussatsen och cosinussatsen.
– Pythagoras sats.
– Likformighet.
– Randvinkelsatsen.
– Inskrivna (cykliska) fyrhörningar.
– Hur man räknar ut arean för olika figurer.
– Eventuellt de tredimensionella kropparnas volym.
– Lådprincipen.

Det är allt jag kan tänka ut på rak arm. Har du några tips?

HMT-kval 2010

Som traditionen är, rättar elever som gått på Danderyds Gymnasium tävlingen HMT varje år. Även elever som gick ut gymnasiet för mer än 6 år sedan…

I helgen rättade vi alla inskickade bidrag och jag fick äran att vara med och rätta uppgift nummer 2 av kvalets problem.

Största delen av rättningen bestod i att rätta ner poängen från maximala 3 till 1 eftersom endast rätt svar (även med kontroll) skulle ge exakt 1 poäng.

Det viktiga i tävlingen är att man kan motivera sina lösningar, och motiveringen motsvarar oftast den större delen av poängen, vilket många elever och lärare tyvärr missar.

Det är ju på samma sätt i livet: det viktigaste är inte resultat, utan vägen dit. Nåväl, nog om livsfilosofi.

Efter rättningens slut bestämdes ett gränspoäng för elever som skulle gå vidare till final. Jag vill gratulera Toomas Liiv, en av de aktiva problemlösarna här på bloggen, som klarade den gränsen! Grattis!!!

Problem 1

Lösning

Problem 2

Lösning

Problem 3

Lösning

Problem 4

Lösning

Problem 5

Lösning

Problem 6

Lösning

Vill du få extrainfo om problemlösning via e-post från Mattebloggen?

Problem 1

Lösning

Kommetarer

Problem 2

Lösning

Kommetarer

Problem 3

Lösning

Kommetarer

Problem 4

Lösning

Kommetarer

Problem 5

Lösning

Kommetarer

Problem 6

Lösning

Kommetarer

Vill du få extrainfo om problemlösning via e-post från Mattebloggen?

Vill du få extrainfo om problemlösning via e-post från Mattebloggen?