Korstal 2015
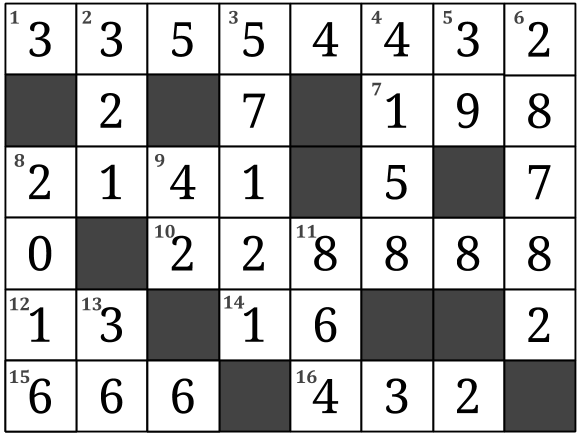
Fyll i precis som ett vanligt korsord (men endast med siffror). Obs! Inga tal börjar med noll.

Vågrätt:
1. En tvåpotens (det vill säga 2n).
7. Har samma siffersumma som vågrätt 15.
8. Talet siffersumma är lika med talets sifferprodukt.
10. Det minsta talet vars alla siffror är jämna som är delbart med vågrätt 7.
12. En delare till lodrätt 5.
14. Ett kvadrattal (det vill säga n2).
15. Alla siffrorna i talet är likadana.
16. Lodrätt 2, ökat med 111.
Lodrätt:
2. Talet siffersumma är lika med talets sifferprodukt.
3. Ett primtal i kvadrat.
4. Vågrätt 8 + vågrätt 14 + vågrätt 15 + vågrätt 16 + lodrätt 5 + lodrätt 11
5. Delbart med vågrätt 12.
6. Lodrätt 2 baklänges multiplicerat med vågrätt 16 baklänges, baklänges.
8. Vågrätt 15 + vågrätt 15 + vågrätt 15 + siffersumman för vågrätt 15
9. Delare till lodrätt 8.
11. Vågrätt 16 dubblat.
13. Ett kvadrattal.
Vad blir summan av korstalets alla trettiosju siffror?
Ladda ner Korstal 2015 som pdf
Korstal 2014
Korstal 2014
Fyll i precis som ett vanligt korsord (men endast med siffror). Obs! Inga tal börjar med noll.

Vågrätt:
1. Delbart med 9
4. Valören på en svensk sedel
5. Alla siffror i talet är likadana
7. Ett kubtal delbar med lodrätt 3
9. Ett tal bestående av siffror som är kvadrattal, där alla sådana siffror förekommer
11. Vågrätt 1 plus vågrätt 5 minus lodrätt 1
Lodrätt:
1. Antalet positiva tvåsiffriga tal
2. Ett palindromårtal i det förflutna
3. En delare till lodrätt 2
4. Vågrätt 1 minus vågrätt 5
5. Vågrätt 1 gånger vågrätt 5
6. Vågrätt 9 plus lodrätt 5
8. En tvåpotens minus lodrätt 1
10. Delbart med lodrätt 3
Ett kvadrattal är kvadrat av ett heltal. Ett kubtal är kub (tredjepotens) av ett heltal. Ett palindromtal är ett tal som ser likadant ut fram- som baklänges. En tvåpotens är 2 multiplicerat med sig själv några gånger (även 1 och 2 räknas som tvåpotenser). Med delbart med N menas att det går att jämnt dela med talet N. Med delare till N menas att N går att dela jämnt på det talet.
Tresiffriga tal
Tresiffriga tal
Korstal 2013
Korstal 2013
[kkratings]
Fyll i precis som ett vanligt korsord (men endast med siffror). Obs! Inga tal börjar med noll.
Lös gärna korstalet tillsammans med familj eller vänner! Ladda ner för utskrift.

Vågrätt:
1. Ett palindromtal som är delbart med sin siffersumma. (Ett palindromtal läses likadant fram- som baklänges.)
5. En delare till lodrätt 11.
6. Har samma siffersumma som lodrät 9.
8. Har exakt samma rest vid division med 2, 3 respektive 5.
10. Vågrätt 8 fördubblat.
12. Minsta gemensamma multipel av 8 och 125.
13. Relativt primt med vågrätt 12.
15. En produkt av fem olika primtal varav det största är 23.
Lodrätt:
2. Ett palindromtal som också är en kub.
3. En faktor i både lodrätt 9 och vågrätt 15.
4. Skrivet i det binära talsystemet förekommer det sju ettor i rad.
6. En trepotens.
7. Vågrätt 8 i kvadrat.
9. Summan av fem på varandra följande årtal från det här århundradet.
11. Numret på året som kommer.
14. Inte ett primtal.
Palindromrebus
Palindromrebus
[kkratings]
I likheten ersätt stjärnorna med siffror, så att likheten blir korrekt, om båda termerna samt summan måste förbli samma tal om man läser dem från höger till vänster. Talen får inte börja med noll.
Datum med träblock
Rekommenderad från: 11 år
[kkratings]
Min bror ställer in datumet varje dag med hjälp av fem träblock.

Tre av dem är av avlånga och används för månaderna.

De andra två är kuber. Vilka siffror kan stå på kubernas sidor för att man ska kunna bilda alla datum?
Korstal 2012
Korstal 2012
[kkratings]
Fyll i precis som ett vanligt korsord (fast nu endast med siffror). Obs! Inga tal börjar med noll.

Vågrätt:
1. Tvåpotens.
6. Siffersumman för lodrätt 13, skrivet baklänges.
7. Närmsta årtalet i framtiden som skrivs med bara två olika siffror.
9. Årtal i det förflutna som var precis emellan två skottår.
10. Siffersumman för vågrätt 15.
11. Delbart med 4 olika primtal.
12. Om jag delar min ålder med 2 och sedan adderar 5, så får jag hur gammal jag var för 8 år sedan. Vilket år är jag född?
15. En kub.
18. Produkten av lodrätt 14 och lodrätt 16.
19. En summa av två olika kvadrattal.
Lodrätt:
1. Delbart med 9.
2. Siffrorna i talet bildar aritmetisk talföljd.
3. Delbart med 10101.
4. Produkten av siffersumman för vågrätt 10 och den positiva sifferdifferensen för vågrätt 10.
5. Talet ser likadant ut vänt upp-och-ner.
8. Siffrorna i talet kommer i avtagande ordning.
13. Ett primtal.
14. Hur gammal blir jag nästa år?
16. Har udda antal delare.
17. Har samma siffersumma som lodrätt 13.
Datum med två siffror
Datum med två siffror
[kkratings]
Dagens datum är lite ovanligt: 121222. Vilket blir nästa datum som skrivs med högst två olika siffror (om datumet betecknas med 6 styken siffror)?
Ett tal med åtta siffror
Ett tal med åtta siffror
[kkratings]
Kan man hitta på ett tal som består av 8 olika siffror, så att talet är delbart med alla siffror som ingår i det?

Bas 10
En alien med 4 fingrar och en människa möter varandra:

Vad är en bas?
De flesta förstår räkning med olika baser utan att behöva lära sig någon formell definition. Vi räknar i bas 10 och det finns ental, tiotal, hundratal och så vidare. Vi har 10 siffror: 0,1,2,3,4,5,6,7,8,9 och varje (naturligt) tal bestäms entydigt av att några siffror skrivs i en viss ordning.
Men vad händer om vi har brist på siffror? Datorerna har bara siffrorna 0 och 1 till exempel. Eftersom det är två siffror säger vi att datorernas tal är skrivna i bas två. De första sju talen skulle då vara: 1,10,11,100,101,110,111. Vad långa talen blir! Så kan det gå när det finns så få siffror. Har vi brist på siffror, måste vi använda fler potisioner.
Vad händer om vi hittar på egna siffror? Låtsas som att vi har sexton siffror: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F. Då kan vi räkna i bas sexton:
Exmpelvis kommer talet 9999 precis före talet A000. Det största sexsiffriga talet är talet FFFFFF och så brukar man beteckna färgen ”vit” hexadecimalt (det vill säga i bas sexton)!
Varför skulle varje bas vara bas 10?
Hur kommer det sig att alienen med fyra fingrar räknade i bas 10? Det är för att han själv tycker att han har 10 fingrar! De första fyra talen skriva i hans bas är nämligen 1,2,3,10 (han har bara fyra siffror).
Detta verkar hända med varje bas. Om vi räknar i bas n, så har vi n siffror (varav t.ex. 0 är den första), vilket betyder att de första n-1 positiva heltalen kan betecknas med bara en siffra. Men för ett tal till (och det blir talet n) behöver vi två siffror! Det minsta tvåsiffriga talet betecknas just 10 (om vi valde just 0 och 1 att beteckna de minsta siffrorna).
Bas ett?
Inga konstigheter verkar ske när vi räknar med bas två eller någon annan större bas. Baserna följer samma räkneregler som vanligt, vi behöver bara hålla reda på vilka siffror som finns tillgängliga.
Men hur skulle man kunna räkna med bas ett? Om det bara är en siffra tillåten, hur ska vi då kunna skriva 10, som ska beteckna vår bas med hjälp av just vår bas?
Det går inte, vi kan bara skriva en symbol, så alla talen måste skrivas olika långa för att vi ska kunna skilja på dem. Om vår symbol är a, så ser våra fem första positiva heltal ut så här: a, aa, aaa, aaaa, aaaaa.
Men ska vi välja en siffra istället för a och i så fall vilken siffra?
Större baser har ju den egenskapen att talen är lätta att ”räkna om” till vårt vanliga bas tio.
T.ex. så är 1011 i bas två lika med
1*8+0*4+1*2+1*1 = 11
i bas tio, och 30A i bas sexton är lika med
3*256+0*16+10*1 = 778
i bas 10.
Hur blir det då med talet aaa i bas 1?
a*1+a*1+a*1 = 3
Då är 3a = 3. Alltså är a=1. Och talet ett i bas ett måste skrivas just 1.
Notera att om alla tal i bas 1 består av 1:or så är det omöjligt att skriva talet 0. Positionssystemet fungerar inte heller som det brukar, eftersom alla positioner står för exakt lika mycket: 1. Tal adderas då genom att skrivas ihop:
111 + 1111 = 1111111.
Om vi vill ha ett talsystem som ska kallas för bas ett och behålla så mycket egenskaper för en bas som möjligt, så har vi hittat det. Vi kan dock omöjligen hitta något som behåller alla egenskaper och kallas för bas 10 i sin egen beteckning.
© 2009-2025 Mattebloggen