På lektionen bevisade vi att vinkelsumman i en godtycklig triangel är 180° och en i fyrhörning 360°. Hur blir det med en femhörning, sexhörning osv.? Och hur bevisar man resultatet?
Det är inte bara månghörningar som har en viss bestämd vinkelsumma, utan andra figurer också. Vad blir vinkelsumman i en stjärna och varför är det alltid så?
Det här är alltså uppgifterna man kan tänka på hemma inför nästa Matteklubben-möte:
• Bestäm vinkelsumman i en n-hörning.
• Bestäm vinkelsumman (av de markerade vinklarna) i en femuddig stjärna.
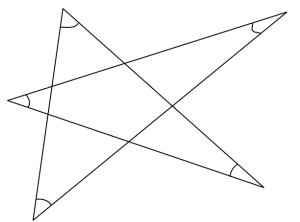

Om man ritar en regelbunden femhörning och gör en stjärna blir de med båge betecknade vinklarna 36 grader och summan av dem blir 180 grader, Den blir 180 grader även om femhörningen är konvex men oregelbunden
Stämmer, men varför blir de 36 grader i det regelbundna fallet. Och ännu mer intressant, varför är summan densamma även om femhörningen är oregelbunden?
När man ritar diagonalerna i en regelbunden femhörning delar de hörnvinklarna i tre lika stora vinklar. 108/3 = 36. Diagonalerna bildar en femuddig stjärna med en regelbunden femhörning i centrum.
Det måste förklaras i så fall varför diagonalerna delar vinkeln i tre lika stora delar.
Visst måste det förklaras. Ritar man en regelbunden sexhörning och drar diagonalerna kommer dessa att dela en hörnvinkel i fyra lika delar 120/4=30
Ritar man en cirkel runt den regelbundna femhörningen kan man använda satsen om periferivinklar och medelpunktsvinklar för att förklara varför 108 delas i tre lika delar. Ritar man en regelbunden sjuhörning kan man konstatera att diagonalerna delar hörnvinkeln i fem lika delar.