Pythagoreiska tripplar i form av areor, del 3

I del 2 såg vi att en primitiv pythagoreisk tripplel alltid kan representeras i form av rektangelareor (inuti rutnätscirklar).

Dyker det upp exakt 3 olika rekatngelareor inuti en sådan cirkel?
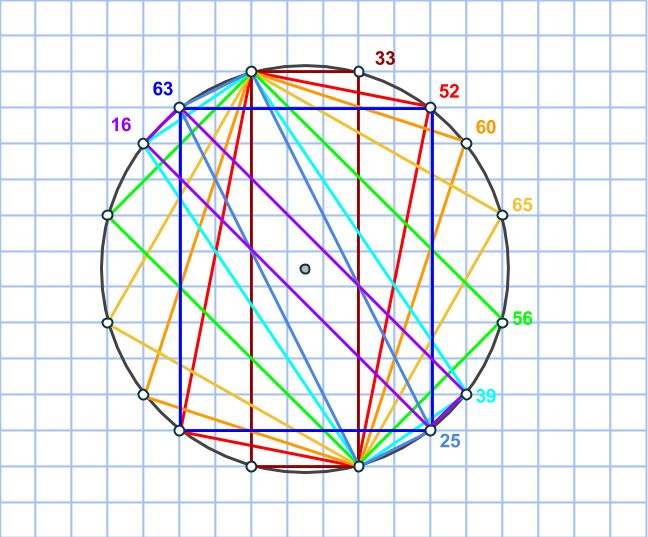
Nej, det kan dyka upp fler än så, vilket beror på att vi kan hitta cirklar där fler än 8 rutnätspunkter hamnar på cirkeln. Nedan ser ni nio olika rektanglar, med areor utskrivna, som vi kan hitta i en cirkel med 16 rutnätspunkter på randen. (Vad tror du förresten är det största antalet rutnätskpunkter man kan hitta på en cirkel?)

Men hur gör man med icke-primitiva Pythagoreiska tripplar? Konstruktionen från förra delen fungerar inte, eftersom icke-primitiva tripplar kan inte genereras på samma sätt från m och n som primitiva.

En icke-primitiv trippel är däremot lika med en primitiv, multiplicerad med en faktor, som till exempel (6,8,10) är trippeln (3,4,5) multiplicerad med faktorn 2. Om vi på något sätt kunde förstora alla rektanlar med faktorn 2, utan att förlora rutnätsegenskaperna, så skulle problemet vara löst. Men förstorlingen av alla rektanglar med faktorn 2 skulle ske om alla sidor förstorades med faktorn √2.

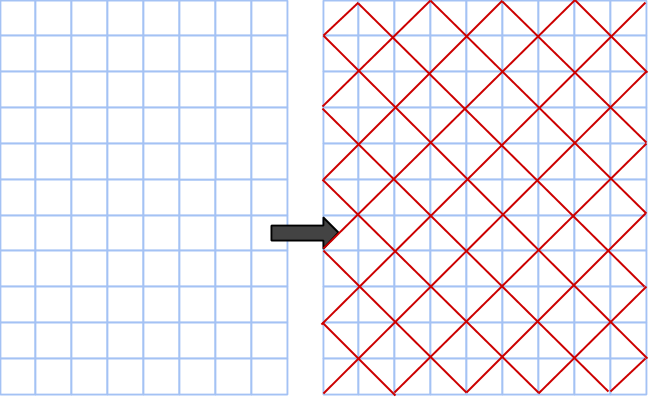
Detta kan vi göra om vi helt enkelt förstorar hela rutnätet med faktorn √2! Vi gör det genom att rotera koordinataxlarna 45 grader och betrakta fyra punkter som bildar en kvadrat med sidan √2 som en enda ruta. På bilden nedan är det nya rutnätet ritat i rött ovanpå det gamla (eftersom vi trots allt använder det gamla för att rita ut cirklar).

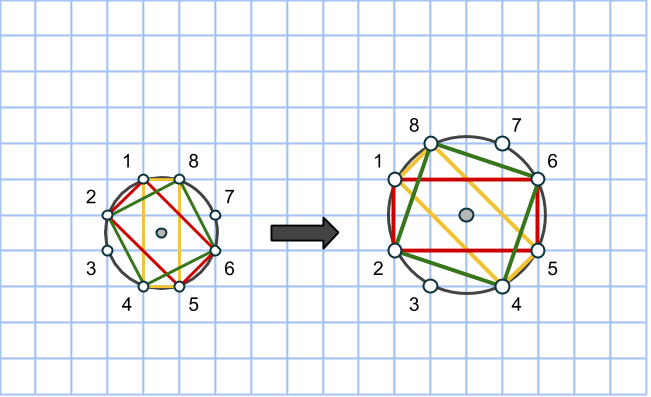
Vi gör samma sak med rutnätscirkeln: rotera och förstora med faktor √2, då bildar från en cirkel med areorna (3,4,5) en annan cirkel med rektangelareorna (6,8,10). Punkterna på cirkeln numreras för det ska gå lättare att se rotationen.

Men såklart kan vi bilda nya rutsystem på andra sätt och med andra rutstorlekar! Bland annat går att att förstora alla areor med 5, med 13 och såklart med produkter av faktorer, som vi redan kan förstora med. (Försök att hitta ett rutsystem med rutlängderna √5). På så vis går det alltså att konstruera alla icke-primitiva taltripplar på formen t.ex. (5*(m²-n²),5*2*m*n,5*(m+n²)).

Men går att förstora på så sätt med alla faktorer? Går det till exempel att konstruera den icke-primitiva trippeln (9,12,15)? Vi besvarar den här frågan i den sista delen.