Matte C – Mattebloggen

Var kommer talet e ifrån?

Jag hade själv länge ingen intuitiv förståelse för $e$ . Jag visste att funktionen $e^x$ hade sig själv som derivata och att funktionen hade en snygg Taylorutveckling. Men inte så mycket vad det hade med naturen att göra.

Tills jag träffade på sidan som förklarar svåra begrepp på ett intuitivt sätt. Sidans författare gick snällt med på att dela med sig av sin förklaring och bilder. Utav det gjorde jag en presentation om talet $e$ på svenska!

Skriv gärna om förklaringen hjälpte dig att förstå $e$ .

Tangent

När jag säger ”tangentlinje” tänker du kanske på någon av dessa bilder:

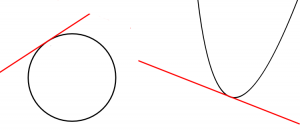
En tangentlinje nuddar precis en kurva i en viss punkt. Ofta har jag tänkt att en tangent aldrig är en sekant, det vill säga att tangenten aldrig kan skära kurvan.

Men vad är då detta för något?

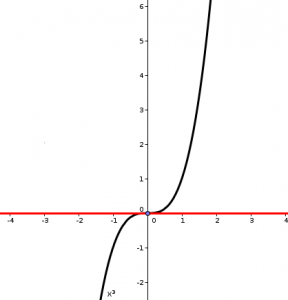
Nu skär ju uppenbarligen den röda linjen kurvan. Det går inte att rita en linje som precis nuddar kurvan i origo, utan att det blir skärning!

Det förklaras med att definitionen på en tangent baserar sig på sekanter, det vill säga vanliga linjer som skär kurvan i några punkter, minst två:

Tangent

En tangent till en kurva i en punkt A är vad sekanterna genom A närmar sig mot, då en annan av sekantens skärningspunkter med kurvan (punkten B) närmar sig A.

Därför blir tangenten i origo till grafen för $y=x^3$ horisontell och vi har en så kallad terasspunkt i origo.

Tangenter till cirklar är speciella: de är vinkelräta mot radien, som ritas från cirkelns mittpunkt till tangeringspunkten!

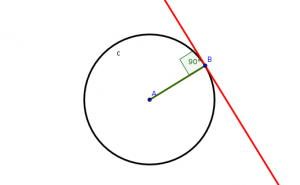
Lutningen på tangenten är viktig, för att den ger oss derivatan i den punkten. Låt oss kolla på lutningen på radien först. För enkelhets skull antag att det är enhetcirkeln vi tittar på.

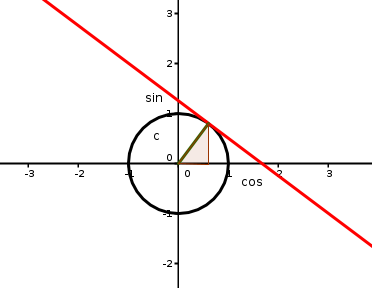
Lutningen är lika med förändringen i y-led delat på förändringen i x-led. Det blir $\frac{sin x}{cos x}$ , det vill säga $tan x$ .

Tangentens lutning måste då vara $\frac{-1}{tan x}$ eftersom tangenten är vinkelrät mot radien. Undrar om det är härifrån namnet ”tangens” kommer ifrån?

Lektion om potenser

Baserat på första lektionen, har jag gjort en presentation om potenser. Drygt hälften av föredraget kommer från den första lektionen jag lade upp, men resten är utfyllt med mer material om potenser. Se för er själva!

Lektion om potenser – tog ungefär 30 minuter tillsammans med diskussion.

Lektioner i matte C

Ett nytt år innebär för mig nya sysselsättningar. Vårterminen 2011 blev jag nämligen för första gången en gymnasielärare!

Jag undervisar en grupp elever i matte C på ett gymnasium i Uppsala och det är då andra halvan av kurser som gäller för min del. Men de första veckorna har vi bara repetitionstillfällen, det vill säga vi repeterar den första halvan av kursen.

Till förra lektionen skapade jag min första power point-presentation någonsin (en beamer-presentation egentligen, dvs gjord i LaTeX). Den använde jag dock inte på lektionen, utan planerar istället att modifiera och utöka den lite och använda på det andra repetitionstillfället.

Kika gärna på min lektion nummer 1, som handlade om förenklingar. För att visa filen som en power point-presentation, öppna pdf-filen, tryck på F5 och bläddra medelst mellanslag eller piltangenterna. Skriv gärna vad ni tycker!