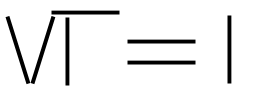Bussar på vägen
Lars går längs med en väg med konstant hastighet. Var 6:e minut ser han en buss som åker förbi honom och var 3:e minut möter han en buss som åker åt andra hållet. Bussarna åker med samma fart åt båda håll och startar från ändhållplatserna med jämna mellanrum. Hur långa är dessa mellanrum?
Ihoplimmad kub
Ihoplimmad kub
Av 27 kuber av storleken 1x1x1 limmade man ihop en kub av storleken 3x3x3 genom att alla kontaktytor limmades. För att limma ihop två sidor använde en droppe lim varje gång. Hur många droppar lim använde man totalt?
Skolsteg
Skolsteg
Maria, Jakob och deras pappa går till skolan tillsammans. Under tiden som pappa tar 3 steg, så tar Maria 5 steg. Under tiden som Maria tar 3 steg, så tar Jakob 5 steg. Maria och Jakob räknade till att de tog 400 steg till skolan tillsammans. Hur många steg tog deras pappa till skolan?
Glassbekymmer
Glassbekymmer
Valentina ville köpa en glass, men saknade 7 kronor. Robert ville köpa samma sorts glass, men saknade 1 krona. Då bestämde de sig för att lägga ihop sina pengar, men även då räckte de inte för att köpa en sådan glass. Hur mycket kostar glassen de ville köpa?
100-våningshuset
Tack till David Nilsson som påminnt mig om en gammal klassiker!
Rekommenderad från: 13 år
En apa är i ett 100-våningshus och vill veta vilken den högsta våningen är som den kan släppa en kokosnöt ifrån utan att den går sönder när det träffar marken. Hur många gånger behöver apan testa att kasta ner en nöt för att garanterat ta reda på det, om den bara har två kokosnötter till godo?

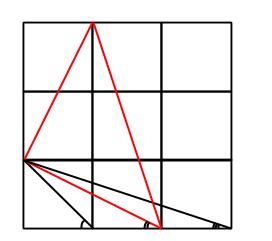
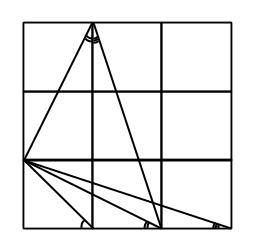
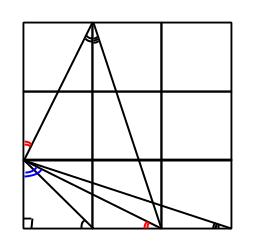
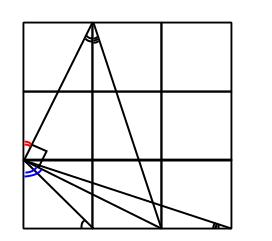
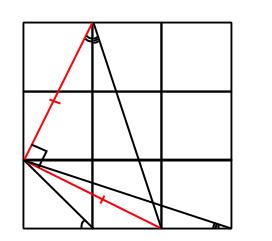
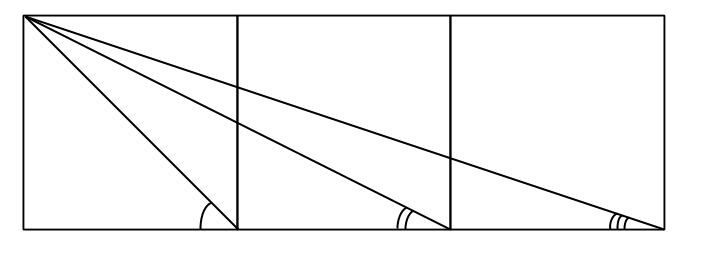
Tre vinklar
Det här roliga problemet har jag fått av min kompis Fredrik från Genikampen-2015!
Rekommenderad från: 15 år
Tre kvadrater är ritade bredvid varandra. Tre linjer dras från ett hörn som bilden visar. Bestäm summan av de tre utsatta vinklarna (i exakt antal grader eller radianer):
Mynten på schackbrädet
Rekommenderad från: 15 år
Du sitter i en fängelsehåla och en vakt kommer till dig med ett erbjudande. Han säger att han kommer lägga upp mynt (totalt 64 st.) på ett schackbräde, ett mynt i varje ruta och det kommer vara slumpat för varje mynt huruvida det ligger med krona eller klave uppåt. Därefter kommer vakten peka på en ruta. Du får sedan en möjlighet att vända upp-och-ner på exakt ett av mynten, vilket du vill.
Därefter kommer en kompis in i rummet, som får se schackbrädet och får gissa vilken ruta vakten pekade på. Gissar han rätt, får ni båda gå fria. Hur kan du och kompisen komma överens om en strategi som garanterar er frihet, oavsett hur vakten gör?

Spionuppdrag
Rekommenderad från: 12 år
En hemlig byggnad består av många rum som ser exakt likadana ut och som är kopplade i en stor ring med små korridorer. I varje rum finns en lampa och en lampknapp. En spion hamnade i ett av rummen. Hur ska han bestämma antalet rum i byggnaden om han bara kan gå runt och tända och släcka ljuset? Från början lyser det i vissa rum, men spionen vet inte på förhand i vilka.

Tändsticksproblem med twist
Det finns många tändsticksproblem som går ut på att flytta tändstickor för att få kvar någon särskild figur eller för att en viss likhet ska uppfyllas. Ett exempel på ett sådant problem kan du hitta i tidningen Forskning och Framsteg.
Här är dock tändsticksproblem som till en början verkar skumma eller omöjliga. Hur många kan du lösa?
1. Ta bort sju tändstickor så att det bara bli sju kvar.
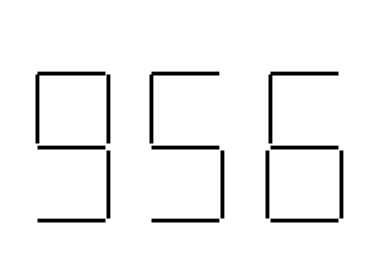
2. Flytta så lite tändstickor som möjligt så att likheten gäller. Tändstickorna får brytas.
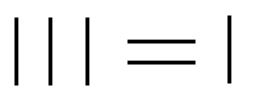
3. Flytta en tändsticka så att likheten gäller.
Korstal 2014
Korstal 2014
Fyll i precis som ett vanligt korsord (men endast med siffror). Obs! Inga tal börjar med noll.

Vågrätt:
1. Delbart med 9
4. Valören på en svensk sedel
5. Alla siffror i talet är likadana
7. Ett kubtal delbar med lodrätt 3
9. Ett tal bestående av siffror som är kvadrattal, där alla sådana siffror förekommer
11. Vågrätt 1 plus vågrätt 5 minus lodrätt 1
Lodrätt:
1. Antalet positiva tvåsiffriga tal
2. Ett palindromårtal i det förflutna
3. En delare till lodrätt 2
4. Vågrätt 1 minus vågrätt 5
5. Vågrätt 1 gånger vågrätt 5
6. Vågrätt 9 plus lodrätt 5
8. En tvåpotens minus lodrätt 1
10. Delbart med lodrätt 3
Ett kvadrattal är kvadrat av ett heltal. Ett kubtal är kub (tredjepotens) av ett heltal. Ett palindromtal är ett tal som ser likadant ut fram- som baklänges. En tvåpotens är 2 multiplicerat med sig själv några gånger (även 1 och 2 räknas som tvåpotenser). Med delbart med N menas att det går att jämnt dela med talet N. Med delare till N menas att N går att dela jämnt på det talet.
© 2009-2025 Mattebloggen