En kung som gillade att bygga

En kung som gillade att bygga

[kkratings]

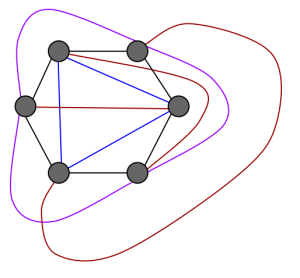
I Sagolandet fanns en kung som tyckte mycket om att bygga. En gång bestämde han sig för att bygga 6 torn och anlägga vägar mellan varje par av torn, men på så sätt
att det bara skulle bildas tre korsningar mellan vägarna. Dessutom fick bara två vägar mötas i varje korsning, aldrig fler.

Hur skulle planen över tornen och vägarna kunna se ut?


Visa lösningen

Rätt antal

Rätt antal

[kkratings]

Fabian sade till Artem att räkna antalet grafer han hade ritat i skrivblocket. ”Ta antalet grafer, addera 7, sedan dividera resultatet med 8, sedan multiplicera med 6 och sedan subtrahera 9. Då kommer du få ett primtal!”

Artem blandade ihop vad Fabian hade sagt till honom. Han räknade antalet grafer rätt, men sedan multiplicerade han det antalet med 7, subtraherade 8 från resultatet, dividerade allt med 6 och sedan adderade 9.
Vad fick han för resultat?

Primtal

Ett primtal är ett positivt heltal som har exakt två delare: 1 och talet självt.

Till exempel är 2, 3, 5 och 7 primtal.

Men 1, 4, 6, 8 och 9 är inte primtal: 1 har endast en delare (1), 4 har tre delare (1, 2, 4), 6 har fyra delare (1, 2, 3, 6), 8 har fyra delare (1, 2, 4, 8) och 9 har tre delare (1, 3, 9).

Visa lösningen

Egentillverkad tärning

Egentillverkad tärning

[kkratings]

Lars tillverkade en tärning, där han satte ut 1, 2, 3, 4, 5 respektive 6 prickar på sidorna. Sedan kastade han tärningen två gånger. Första gången blev summan av alla prickar på de fyra stående sidorna lika med 12, den andra gången blev den lika med 15.

Hur många prickar finns på sidan som ligger mittemot sidan med 3 prickar?

Visa lösningen

Uppdelad rektangel

Uppdelad rektangel

[kkratings]

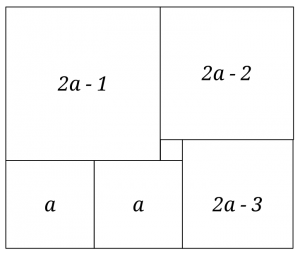
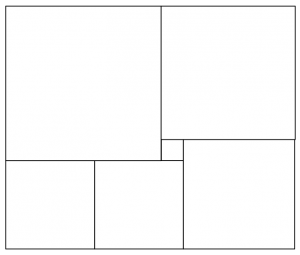
En rektangel är uppdelad i 6 kvadrater (se bilden nedan). Hur stor är den största kvadraten om den minsta har sidlängden 1cm?

Obs! Figuren är inte nödvändigvis perfekt, därför räknas det inte som en lösning att mäta längderna.

Visa lösningen

Fyra lika kompisar

Fyra lika kompisar

[kkratings]

Fyra kompisar är lika varandra på många sätt: vilket par av dem man än tittar på, så har det paret samma tilltalsnamn eller samma efternamn eller samma födelsedatum. Däremot har inga tre av kompisarna samma tilltalsnamn, inga tre har samma efternamn och inte heller finns det tre med samma födelsedatum.

Kan sådana här fyra kompisar finnas?

Visa lösningen

Två magiska tal

Två magiska tal

[kkratings]

Finns det två tal, sådana att deras summa, produkt, samt kvot sammanfaller?

Visa lösningen

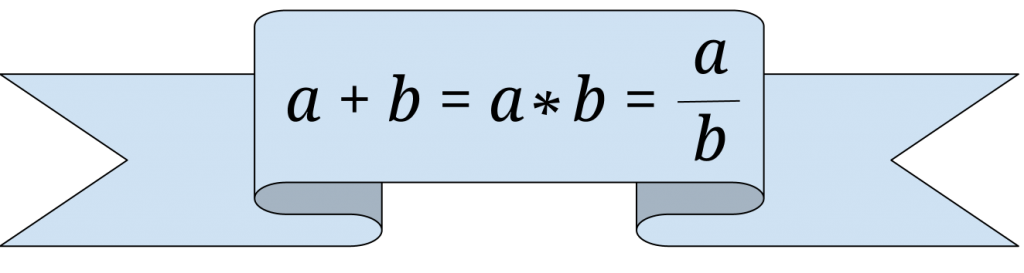
Trassel (tangles)

Aktiviteten trassel

Rekommenderas för: gymnasieet, universitetet (eller i förenklad form för högstadiet)

Materiel: två stora rep eller sladdar (gärna av olika färger), en ogenomskinlig plastpåse

Tid: 45 minuter

Antalet deltagare: 4 + publik

Aktiviteten ”trassel” kommer från matematikern och pusselkonstruktören Johan Conway och har genomförts i Sverige på bland annat Sonja Kovalevsky-dagarna. Den passar att genomföra på en matematiklektion om bråkräkning/gruppteori eller som en extra matematikaktivitet.

Man börjar med att fyra elever ställer sig som hörnen på en kvadrat inför resten av klassen. Var och en av dem tar tag i var sin ände av ett rep så att repen hänger parallella med hur publiken sitter. Under experimentet får de aldrig släppa sin ände.

Så här ser det ut uppifrån (Positionerna närmast klassen är D och C):

trassel start

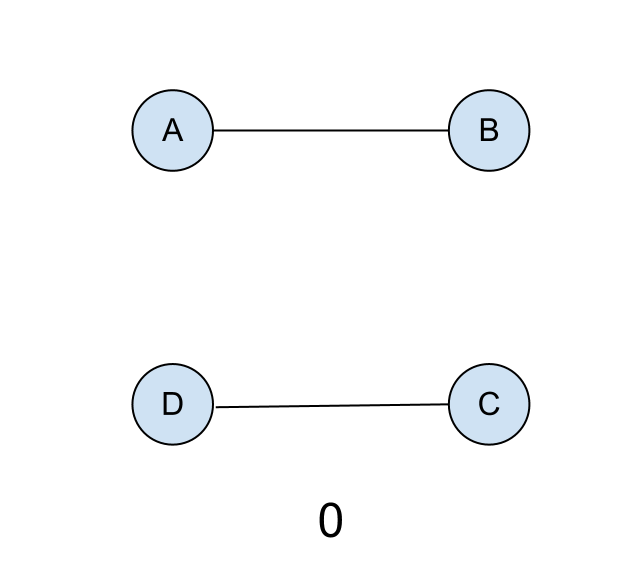
Nu kommer de fyra personerna utföra en slags dans och trassla till repen samtidigt. Varje trassel (tangle) repen bildar kommer att ha ett motsvarande tal. Från början, när repen är parallella mot varandra och mot klassen, motsvarar det talet 0.

Det första tillåtna danssteget är att vrida om repen runt varandra. Och inte på vilket sätt som helst, utan det måste göras av personerna som står på positionerna B och C. Dessa två personer byter plats med varandra och B är den som lyfter sin repände, som C går under för att komma till sin nya position.

vrida om

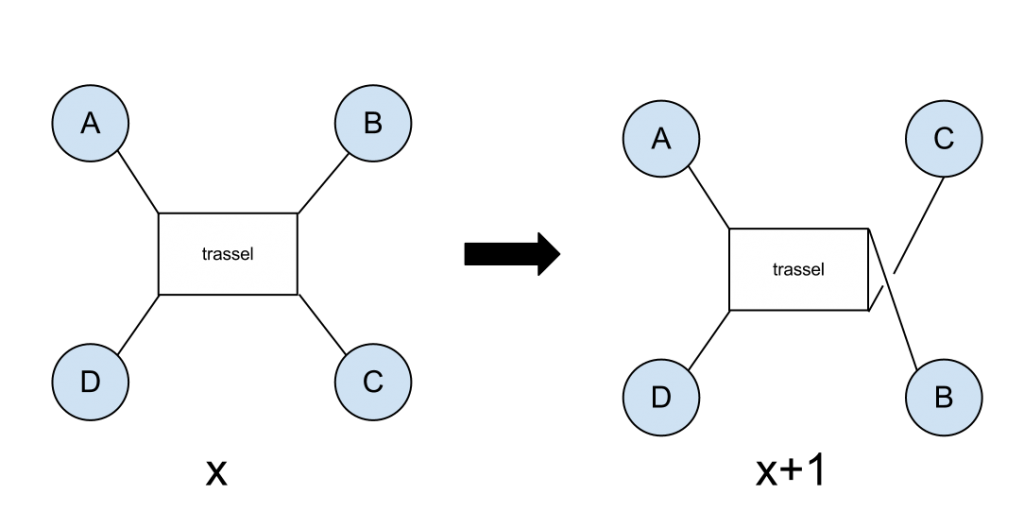
Att vrida om trasslet på det här sättet kommer att öka talet med 1. Så en omvridning ger ett trassel med värdet 1, medan en till omvridning ger talet 2 osv.

Det andra tillåtna danssteget är att rotera medurs. Person A går till position B, person B går till position C och så vidare.

Att rotera trasslet kommer också att förändra talet. Men hur? Om elevera har hållit på med funktioner och algebra tidigare kan man låta dem att lista ur svaret. Annars kan man helt enkelt säga att talet x omvandlas till talet -1/x vid en sådan rotation. Notera t.ex. att två rotationer i rad inte gör någon skillnad på trasslet, vilket är klart för trassel som består av några omvridningar:

n -> -1/n -> -(1/(-1/n)) = n

rotera

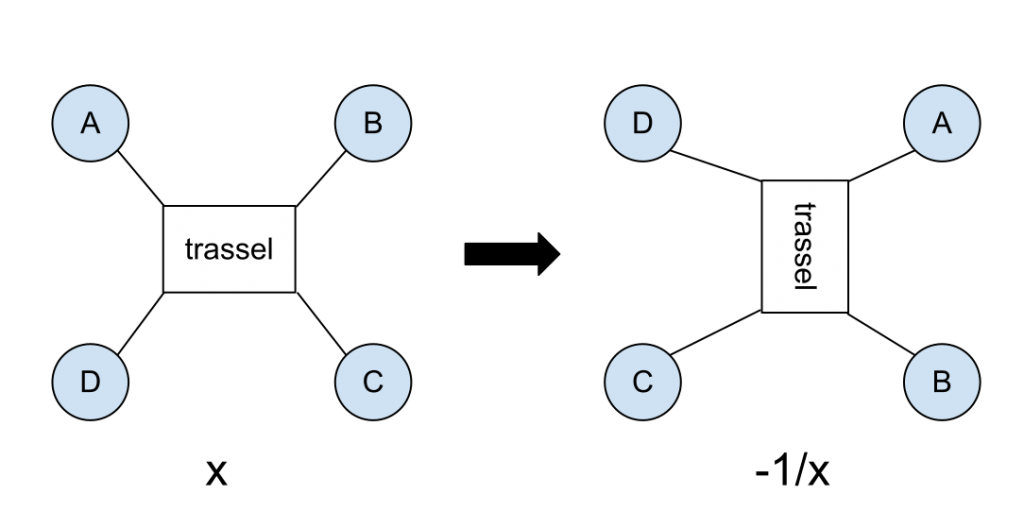
När alla har förstått reglerna kan man be eleverna att uföra några danssteg (börja med att först
vrida om), samtidigt som man räknar på talet som ska motsvara trasslet. Om man från början gör dansstegen: vrida om, vrida om, rotera, vrida om, vrida om, vrida om, rotera, vrida om så kommer man till talet:

0 -> 1 -> 2 -> -1/2 -> 1/2 -> 3/2 -> 5/2 -> -2/5 -> 3/5

Hur ska man lösa upp detta trassel om man bara tillåts att göra dansstegen ovan? Publiken får lösa denna uppgift genom att försöka räkna ut hur man ska göra med bråket 3/5 för att det ska bli 0, om man bara tillåts addera 1 och ta den negativa inversen. Man kan ju inte göra dansstegen ”baklänges”, eftersom steget ”att vrida runt åt andra hållet” inte finns.

När någon har kommit på dansstegsföljden kan man testa dansen och se att knuten verkligen löses upp.

Det här kan man göra med andra tal. Ju svårare trasslet är, desto roligare blir det att se det lösas upp. När repen är tilltrasslade, kan man knyta några plastpåsar runt dem, så att trasslet inte syns och sedan utföra dansstegen som eventuellt ska lösa upp trasslet. När talet på tavlan är 0 kan man knyta upp påsarna och se att allt blir som i början, bara man drar i repen!

Fler frågor att diskutera på avancerad nivå:

– Vad händer om man roterar först? Vad är talet -1/0 och vad har det för egenskaper? Ska trasslet -1/0 förändras om man vrider om det?

– Hitta inversen till att vrida om. Det vill säga, om man startar från ett trassel och sedan vrider om en gång, vad för danssteg skall man göra för att komma tillbaka till starttrasslet?

Fler frågor för att grupper:

– Om man börjar från 0, hur kommer man till ett specifikt trassel, t.ex. -3?

– Hut kommer man snabbast ner till 0 från ett specifikt trassel? Här kan eleverna tävla om vem som kan hitta på kortaste dansstegsekvensen när trasslet är ett relativt avancerat bråktal.

Mer om aktiviteten kan du läsa i Conways text (tangles börjar på sida 10) conway.pdf, samt Tom Davis text med utförlig diskussion och beskrivning av aktiviteten. tangle.pdf.

Tack till Johan Björklund för tipset!

Klurig fyrhörning

Rekommenderad från: 17 år

[kkratings]

En konvex fyrhörning ABCD har kända sidlängder: AB = 5, BC = 10, CD = 14, DA = 11. Fyrhörningens diagonaler skär varandra med en viss vinkel. Hur stor är den vinkeln?

Visa lösningen

Bas 10

En alien med 4 fingrar och en människa möter varandra:

Vad är en bas?

De flesta förstår räkning med olika baser utan att behöva lära sig någon formell definition. Vi räknar i bas 10 och det finns ental, tiotal, hundratal och så vidare. Vi har 10 siffror: 0,1,2,3,4,5,6,7,8,9 och varje (naturligt) tal bestäms entydigt av att några siffror skrivs i en viss ordning.

Men vad händer om vi har brist på siffror? Datorerna har bara siffrorna 0 och 1 till exempel. Eftersom det är två siffror säger vi att datorernas tal är skrivna i bas två. De första sju talen skulle då vara: 1,10,11,100,101,110,111. Vad långa talen blir! Så kan det gå när det finns så få siffror. Har vi brist på siffror, måste vi använda fler potisioner.

Vad händer om vi hittar på egna siffror? Låtsas som att vi har sexton siffror: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F. Då kan vi räkna i bas sexton:
Exmpelvis kommer talet 9999 precis före talet A000. Det största sexsiffriga talet är talet FFFFFF och så brukar man beteckna färgen ”vit” hexadecimalt (det vill säga i bas sexton)!

Varför skulle varje bas vara bas 10?

Hur kommer det sig att alienen med fyra fingrar räknade i bas 10? Det är för att han själv tycker att han har 10 fingrar! De första fyra talen skriva i hans bas är nämligen 1,2,3,10 (han har bara fyra siffror).

Detta verkar hända med varje bas. Om vi räknar i bas n, så har vi n siffror (varav t.ex. 0 är den första), vilket betyder att de första n-1 positiva heltalen kan betecknas med bara en siffra. Men för ett tal till (och det blir talet n) behöver vi två siffror! Det minsta tvåsiffriga talet betecknas just 10 (om vi valde just 0 och 1 att beteckna de minsta siffrorna).

Bas ett?

Inga konstigheter verkar ske när vi räknar med bas två eller någon annan större bas. Baserna följer samma räkneregler som vanligt, vi behöver bara hålla reda på vilka siffror som finns tillgängliga.

Men hur skulle man kunna räkna med bas ett? Om det bara är en siffra tillåten, hur ska vi då kunna skriva 10, som ska beteckna vår bas med hjälp av just vår bas?

Det går inte, vi kan bara skriva en symbol, så alla talen måste skrivas olika långa för att vi ska kunna skilja på dem. Om vår symbol är a, så ser våra fem första positiva heltal ut så här: a, aa, aaa, aaaa, aaaaa.
Men ska vi välja en siffra istället för a och i så fall vilken siffra?

Större baser har ju den egenskapen att talen är lätta att ”räkna om” till vårt vanliga bas tio.
T.ex. så är 1011 i bas två lika med

1*8+0*4+1*2+1*1 = 11

i bas tio, och 30A i bas sexton är lika med

3*256+0*16+10*1 = 778

i bas 10.

Hur blir det då med talet aaa i bas 1?

a*1+a*1+a*1 = 3

Då är 3a = 3. Alltså är a=1. Och talet ett i bas ett måste skrivas just 1.

Notera att om alla tal i bas 1 består av 1:or så är det omöjligt att skriva talet 0. Positionssystemet fungerar inte heller som det brukar, eftersom alla positioner står för exakt lika mycket: 1. Tal adderas då genom att skrivas ihop:

111 + 1111 = 1111111.

Om vi vill ha ett talsystem som ska kallas för bas ett och behålla så mycket egenskaper för en bas som möjligt, så har vi hittat det. Vi kan dock omöjligen hitta något som behåller alla egenskaper och kallas för bas 10 i sin egen beteckning.

Kvaternioner

Enligt en broinskription (se bilden nedan) upptäcktes kvaternionerna för exakt 169 år sedan, då William Hamilton tog en promenad i Dublin med sin fru. Hamilton kände till de komplexa talen (till exempel talet i som uppfyller likheten i\cdot i = -1), men han ville utvidga dem ytterligare till en större talmängd, som fortfarande skulle uppfylla de viktigaste talegenskaperna.

Han kom då på mängden kvaternioner (betecknas \mathbb{H}), som förutom vanliga tal och i även innehåller talen j och k, som uppfyller följande:

(i\cdot i = -1 , denna egenskap är kvar från de komplexa talen)
j\cdot j = -1
k\cdot k = -1

i\cdot j = k
j\cdot k = i
k\cdot i = j

Det spelar förstås ingen roll vilka bokstäver man väljer att beteckna de här nya talen med, det viktiga är deras egenskaper och samverkan med varandra.

Notera att multiplikationen talen emellan är lite märklig. Desto märkligare är att i\cdot j inte blir samma sak som j\cdot i, det vill säga Hamilton lyckades inte behålla multiplikationens kommutativitet. Man adderar och subtraherar dock kvaternioner precis på samma sätt som man skulle göra med de komplexa talen. Man kan addera de olika bokstäverna med varandra och exempelvis gäller:
(1+2i+j) + (2+i-j+k) = 3+3i+k

Hur kan vi lista ut vad j\cdot i bör bli lika med? Tänk på att vi inte kan byta plats på faktorerna, men vi kan multiplicera med något nytt ”från vänster” eller ”från höger”. Säg att vi multiplicerar med i från höger:

(j\cdot i)\cdot i = j\cdot (i\cdot i) = j\cdot (-1)=-j

Så att vårt svar multiplicerat med i från höger ska också vara lika med -j. Vad kan det vara för tal?
Om du inte kan komma på det, tänk på vilket tal multiplicerat med i från höger blir lika med j istället och modifiera svaret efter det.

Man kan göra en liten grundmultiplikationstabell för de komplexa talen:

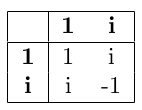
Kan du lista ut vad som står istället för frågtecknen i multiplikationstabellen för kvaternionerna?

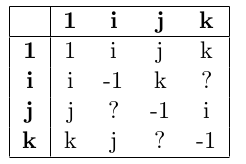
En övning i kvaternioner: Vad blir (1+i+j)(2-j+k)?

Det går att dividera kvaternioner med varandra, resultatet av en division blir alltid ett kvaterniontal (så länge man inte dividerar med 0).

En till övning: Vad blir 1/(i+j) för kvaterniontal?

© 2009-2024 Mattebloggen